| Försök# | Individ 1 | Individ 2 | Medelvärde | Medelvärde ≥ 110? |
|---|---|---|---|---|
| 1 | 91,0 | 100,0 | 95,5 | Nej |
| 2 | 103,0 | 97,0 | 100,0 | Nej |
| 3 | 114,0 | 92,0 | 103,0 | Nej |
| 4 | 73,0 | 98,0 | 85,5 | Nej |
| 5 | 103,0 | 102,0 | 102,5 | Nej |
| 6 | 95,0 | 90,0 | 92,5 | Nej |
| 7 | 89,0 | 135,0 | 112,0 | Ja |
| 8 | 102,0 | 109,0 | 105,5 | Nej |
| 9 | 109,0 | 93,0 | 101,0 | Nej |
| 10 | 97,0 | 107,0 | 102,0 | Nej |
| ... | ... | ... | ... | ... |
| 1e+05 | 90,0 | 103,0 | 96,5 | Nej |
9 Teorin bakom: Sannolikheter
17. Sannolikheter, del 1
18. Sannolikheter, del 2
19. Sannolikhetsfördelningar
20. Binomialfördelningen
21. Normalfördelningen
22. Samplingfördelningen för ett medelvärde
När vi använder data för att dra generella slutsatser så finns det nästan alltid en viss mån av osäkerhet med i bilden. De mönster vi ser i data uppstår som en kombination av verkliga fenomen och slumpmässig variation, vilket innebär att våra slutsatser alltid är osäkra. Vår uppgift är att kvantifiera den osäkerheten. Exempel: Anta att vi följer 10 rökare över livet och att alla dör innan de fyllt 70. Anta vidare att 90 procent av befolkningen överlag får uppleva sin 70-årsdag. Vilken slutsats kan vi dra av detta? Jo, först kanske vi vill veta hur sannolikt det är att 10 individer - utvalda på måfå – dör före 70 (den är 0,110). Eller med andra ord: Det mönster vi ser i data kan inte enkelt bortförklaras med “slumpen”. När vi väl vet detta kan vi fundera vidare över den svårare frågan: vad detta potentiellt säger om rökning.
Det här korta exemplet visar hur sannolikhetsläran ligger som grund för all statistisk slutledning. Men att förstå sannolikheter är också viktigt i andra sammanhang. Alltid när du fattar ett beslut så måste du väga fördelar mot risker. Ska man låta sin katt gå utomhus i stan? Vem ska man anställa som chefekonom? Hur ska Finland agera när en pandemi bryter ut? Nästan alla beslut innefattar osäkerhet. Nobelpristagarna Kahneman och Tversky har visat att människor överlag har en ganska dålig känsla för sannolikheter och risker, vilket gör att vi kanske inte alltid fattar de bästa besluten. Men detta gäller också erfarna experter. Nedan ges fyra exempel på situationer där lekmän och experter ofta bedömer sannolikheter fel.
En person beskrivs på följande sätt: “Steve är mycket blyg och tillbakadragen, alltid hjälpsam men ointresserad av både människor och den verkliga världen. Han är ödmjuk och noggrann, tycker om ordning och struktur, och har ett sinne för detaljer.” Är det mer sannolikt att Steve är bibliotekarie eller bonde? (exemplet konstruerat av Kahneman och Tversky)
Anta att medicin A har dubbelt större risk för en mycket allvarlig biverkning än medicin B. Hur orolig borde du vara om din läkare skriver ut medicin A åt dig?
På ett nationellt prov i matematik används många flervalsfrågor. En elev har fått alla rätt på rekordfart. Sannolikheten för att en elev ska klara alla frågorna på den korta tiden är en på hundratusen. Kan vi anta att eleven fuskat?
En ovanlig men farlig genetisk sjukdom drabbar en på femtusen. Om du har den farliga mutationen så förväntas du insjukna i medelåldern och dö före du fyllt 50. I barndomen tar alla ett diagnostiskt test som har 99-procentig träffsäkerhet. Resultatet var positivt för dig. Borde du vara orolig?
Låt oss nu se på hur man kan resonera i dessa exempel:
De allra flesta svarar här att Steve troligtvis är bibliotekarie. Karaktärsdragen stämmer bättre överens med en typisk bibliotekarie än med en typisk bonde. Men vi ska inte heller glömma att det finns långt fler manliga bönder än manliga bibliotekarier. Antalet manliga bönder som stämmer överens på karaktärsbeskrivningen är antagligen större än antalet manliga bibliotekarier som gör detsamma. Och det är denna jämförelse som är relevant för att besvara frågan.
Det beror på. Anta att risken för en allvarlig biverkning är en på miljonen med medicin B (och därmed två på miljonen med medicin A). Då är det kanske inget att bry sig om. Men om risken är 10 procent med medicin B (och därmed 20 procent med medicin A) så spelar det roll.
För att kunna säga något om saken så bör vi först fråga oss hur många elever som skrivit provet totalt sett. Anta att det är frågan om 100 000. I så fall finns det ingen anledning att tro att eleven ifråga fuskat. Tvärtom – då skulle vi ju förvänta oss att det finns någon elev som faktiskt fått alla rätt på rekordfart.
Nej, det finns ingen större anledning till panik. Sannolikheten att du har den farliga mutationen är ungefär två procent. Vi kan se det genom följande tankeexperiment. Tänk dig en befolkning som består av 10 miljoner personer. Då är 2000 drabbade av den farliga mutationen, och resten (ca 10 miljoner personer) är friska. Bland de drabbade får 1980 personer ett positivt resultat (99 %); bland de friska får ca 100 000 ett positivt resultat (1 %). Risken är alltså relativt liten för att du är en av de 1980 sjuka personerna istället för en av de 100 000 friska.
Osäkerhet och sannolikheter genomsyrar så gott som varje beslut vi fattar, och ligger som grund till statistisk inferens. I nästa kapitel ska vi se närmare på teorin bakom hypotesprövning. Därför ska vi först ta oss tiden att fundera på sannolikheter. Vi ska då börja med att se vad en sannolikhet egentligen är.
9.1 Vad är en sannolikhet?
Vad menar vi egentligen när vi säger att sannolikheten för att dra ett rött kort ur en kortlek är 50 procent, eller att sannolikheten för att få en trea på ett tärningskast är en sjättedel? Låt oss stanna upp vid den här frågan ett litet tag. Vi kan då börja med att konstatera att dessa uttalanden inte handlar om den fysiska världen i sig. Om vi antar en deterministisk världsbild så finns det bara en sak som kan hända; antingen får vi ett rött kort eller ett svart kort; antingen får vi en trea på tärningskastet eller något annat utfall. Det som slutligen hände var förutbestämt av fysikens lagar. Sannolikheter har alltså snarare med oss som människor att göra och vår okunskap gällande vad som kommer att ske. Sannolikhetsläran är den gren inom matematiken som tagit sig an uppdraget att formalisera den här okunskapen. Låt oss se vad sannolikhetsläran går ut på i ett nötskal.
Sannolikhetslära i ett nötskal
Nedan ser du ett venndiagram. Vi brukar använda dem som ett stöd när vi tänker kring sannolikheter. De illustrerar allt det som kan hända när vi utför ett slumpmässigt försök. Anta att vi har en kurs med 15 studerande. Vi väljer slumpmässigt ut en studerande från den här kursen (det är vårt slumpmässiga försök). Då finns det 15 möjliga utfall, representerat av prickar i figuren nedan. Vi kan gruppera dessa utfall på olika sätt (“studenten är en kvinna”, “studenten är vänsterhänt”, “studenten är ekonom”, osv.) Vi brukar kalla en sådan grupp av utfall för en händelse; de enskilda utfallen brukar ofta benämnas element. I figuren nedan har vi ritat ut två sådana händelser: “studenten är en kvinna” (området betecknat med A) och “studenten är vänsterhänt” (området betecknat med B). Klassen har alltså 7 kvinnor och 4 vänsterhänta, varav 2 är kvinnor.
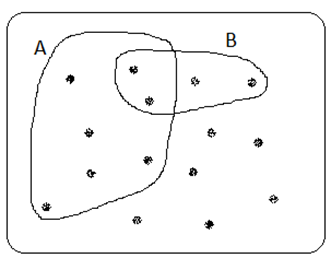
För att komma vidare behöver vi sätta upp några grundläggande regler kring hur sannolikheter fungerar. Nedan ser du de tre axiom som matematikern Kolmogorov beskrev år 1933:
Sannolikheten för ett visst utfall är alltid minst noll.
Sannolikheterna för de olika utfallen summerar till ett.
Om händelserna A och B inte innehåller något gemensamt element så är sannolikheten för A eller B summan av de enskilda sannolikheterna: P(A\(\cup\)B) = P(A) + P(B).
Tecknet \(\cup\) kallas för “union”. Vi använder detta som beteckning för “eller”, dvs. att ett element ska tillhöra grupp A eller B (eller båda). P(A\(\cup\)B) utläses som “sannolikheten för att A eller B ska inträffa”.
Exempel forts. Hur stor är sannolikheten för att en slumpmässigt utvald student från kursen ska vara kvinna eller vänsterhänt, P(kvinna \(\cup\) vänsterhänt)? Svar: 9/15.
Detta illustreras i figuren nedan. Totalt 9 av 15 studerande är kvinnor eller vänsterhänta (alla de som ligger i det gula området): 7 kvinnor + 4 vänsterhänta – 2 som är både och (vi får alltså dra ifrån 2 så att vi inte räknar dessa personer två gånger).
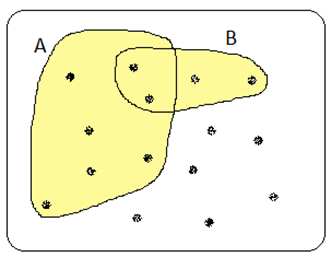
Ovanstående är ett exempel på det som kallas för additionsregeln. Du kanske känner igen den regeln från skoltiden. Vi brukar beskriva den så här:
\[P(A \cup B) = P(A) + P(B) - P(A \cap B)\]
där \(P(A \cap B)\) betecknar sannolikheten för att A och B ska inträffa samtidigt (personen är både kvinna och vänsterhänt). Det omvända u:et, \(\cap\), kallas ibland för “snittet”. I det här exemplet gäller att snittsannolikheten, P(kvinna \(\cap\) vänsterhänt), är 2/15, vilket illustreras i figuren nedan. Additionsregeln visar då att sannolikheten är 9/15 för att en person ska vara kvinna eller vänsterhänt (men det visste vi ju redan!):
\[P(kvinna \cup vänster) = \underbrace{P(kvinna)}_{7/15} + \underbrace{P(vänster)}_{4/15} - \underbrace{P(kvinna \cap vänster)}_{2/15} = \frac{9}{15}\]
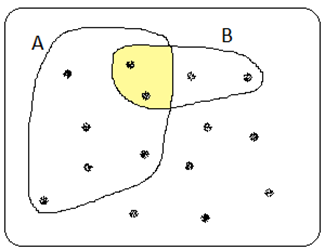
Förutom unioner och snittsannolikheter, så talar vi också om betingade sannolikheter: P(A|B), alltså sannolikheten för A givet B. Eller med andra ord: Hur stor är sannolikheten för A om vi vet att B inträffat?”
Exempel forts. Hur stor är sannolikheten för att studenten är en kvinna, om vi vet att den här studenten är vänsterhänt? Frågan figuren ovan ser vi att 2 av totalt 4 vänsterhänta är kvinnor; den sökta sannolikheten är då 0,5.
Vi kan också ta hjälp av följande formel för att komma fram till samma sak. Den betingade sannolikheten för A givet B ges av:
\[P\left( A \middle| B \right) = \frac{P(A \cap B)}{P(B)}\]
I detta exempel:
\[P\left( kvinna \middle| vänsterhänt \right) = \frac{P(kvinna \cap vänsterhänt)}{P(vänsterhänt)} = \frac{2/15}{4/15} = \frac{2}{4} = 0,5\]
Dylika formler kan vara ett stöd ibland, men om du tycker att det är lättare att resonera dig fram till svaret (utan formler) så är det förstås lika bra så!
Exempel. En kurs innehåller två examinerande moment: tentamen och uppsats. För godkänd kurs krävs att båda momenten är godkända. Sannolikheten för att bli godkänd i tentamen är 80 procent; sannolikheten för att bli godkänd i uppsatsen är också 80 procent. Bland de som blir godkända i uppsatsen är det 95 procent som blir godkända i tentamen. Hur stor är sannolikheten att en studerande blir godkänd i kursen? Svar: 0,76.
Intuitionen: Anta att det är frågan om 100 studerande varav 80 klarar uppsatsen. 95 procent av dessa klarar dessutom tentamen, alltså 76 personer. Sannolikheten för att klara båda blir således 76 procent.
Låt oss också se på “formellösningen”. Nedan ser du formeln för en betingad sannolikhet, men här är vi intresserade av snittsannolikheten som ges i rött, dvs. sannolikheten för att bli godkänd i både tenten och uppsatsen:
\[P\left( G\ i\ tent \middle| G\ i\ uppsats \right) = \frac{\color{red}{{P(G\ i\ tent \cap G\ i\ uppsats)}}}{P(G\ i\ uppsats)}\]
Detta ger:
\[{\color{red}{P(G\ i\ tent \cap G\ i\ uppsats)}} = \underbrace{P\left( G\ i\ tent \middle| G\ i\ uppsats \right)}_{0,95} \times \underbrace{P(G\ i\ uppsats)}_{0,8} = 0,76\]
Exempel forts. Anta som tidigare att 80 procent klarar uppsatsen och 80 procent tentamen. Men nu tänker vi oss att händelserna är oberoende: Om du klarar uppsatsen så ändrar detta inte på sannolikheten för att klara tenten – den är fortsättningsvis 80 procent. Hur stor är nu sannolikheten för att klara kursen? Svar: 0,64.
Intuitionen: Anta som tidigare att det är frågan om 100 studerande varav 80 klarar uppsatsen; bland dessa är det 80 procent som klarar tentamen, alltså 64 personer. Sannolikheten för att klara båda blir således 64 procent.
Formellösningen:
\[{\color{red}{P(G\ i\ tent \cap G\ i\ uppsats)}} = {\color{blue}{P\left( G\ i\ tent \middle| G\ i\ uppsats \right)}} \times P(G\ i\ uppsats)\]
\[ = \underbrace{\color{blue}{P(G\ i\ tent)}}_{=0,8} \times \underbrace{P(G\ i\ uppsats)}_{=0,8} = 0,64 \]
Ovanstående kallas ibland för multiplikationsregeln: Om vi har två (eller fler) oberoende händelser så får vi snittsannolikheten genom att multiplicera ihop de enskilda sannolikheterna. I exemplet ovan fick vi sannolikheten för att bli godkänd i kursen genom att multiplicera ihop sannolikheten för att bli godkänd i tentamen med sannolikheten för att bli godkänd i uppsatsen (0,8*0,8 = 0,64). Detta gäller dock inte om händelserna är beroende. Vi såg också ett exempel på detta tidigare. När sannolikheten för att bli godkänd i tentamen ökade till 95 procent givet att du blivit godkänd i uppsatsen, så fick vi snittsannolikheten genom att multiplicera denna betingade sannolikhet med sannolikheten för att bli godkänd i uppsatsen (0,95*0,8 = 0,76). Låt oss se på ytterligare ett exempel för att belysa skillnaden.
Exempel. Du ska åka till Stockholm en helg i oktober (lördag, söndag). Sannolikheten att det regnar i Stockholm en dag i oktober är 40 procent. Hur stor är då sannolikheten att det regnar båda dagarna, om vi antar (i) att händelserna är oberoende: om det regnar en dag så varken ökar eller minskar detta på risken att det också regnar nästa dag, och (ii) att händelserna är beroende: om det regnar en dag så är sannolikheten för regn nästa dag 60 procent.
I det första fallet (i) så är svaret 0,16. Intuitionen: Risken att det regnar på lördag är 40 procent, och i 40 procent av alla dessa fall så regnar det dessutom på söndag:
P(regn båda dagarna) = 0,4\(\times\)0,4 = 0,16.
I det andra fallet (ii) så är svaret 0,24. Intuitionen: Risken att det regnar på lördag är 40 procent, och i 60 procent av dessa fall så regnar det dessutom på söndag:
P(regn båda dagarna) = 0,4\(\times\)0,6 = 0,24.
Exempel forts. Hur stor är då sannolikheten för att det är uppehåll åtminstone en av dagarna? Svar: Om sannolikheten för regn båda dagarna är 0,16 så är sannolikheten för uppehåll åtminstone en av dagarna 0,84.
Här har vi utnyttjat det som kallas för komplementregeln. Om det inte regnar båda dagarna så måste det ju vara uppehåll åtminstone en av dagarna. Sannolikheten för detta blir då ett minus sannolikheten för att det regnar båda dagarna.
Exempel. Hur stor är sannolikheten för att bara få sexor om vi kastar en tärning fem gånger på raken? Svar: ca 0,00013.
Intuitionen: Anta att vi utför detta experiment – kastar en tärning fem gånger på raken – totalt 90 000 gånger. På första kastet får vi en sexa i 15 000 fall (en sjättedel av fallen). Bland dessa 15 000 fall så resulterar 2500 i en sexa även på andra kastet (=15000*1/6). Bland dessa 2500 fall så resulterar ca 417 i en sexa på tredje kastet (=2500*1/6). Bland dessa får vi en sexa på fjärde kastet i ca 69,5 fall (=417*1/6). Och bland dessa är det slutligen ca 12 som resulterar i sexor på sista kastet. Vi slutade alltså med 12 fall och började med 90 000. Sannolikheten är då 12/90000 (bortsett från lite avrundningsfel på vägen). Vi kunde också beräkna den sannolikheten direktare som:
\[P(fem\ 6:or\ på\ raken) = \frac{1}{6} \times \frac{1}{6} \times \frac{1}{6} \times \frac{1}{6} \times \frac{1}{6} = \left( \frac{1}{6} \right)^{5} \approx 0,00013\]
Notera att vi här utnyttjar multiplikationsregeln. Händelserna är ju oberoende: sannolikheten för att få en sexa på ett kast beror inte på vad som hänt tidigare. Vi får då den sökta sannolikheten genom att multiplicera ihop de enskilda sannolikheterna.
Exempel forts. Hur stor är då sannolikheten för att få nedanstående sekvens?
3, 5, 1, 2, 6
Svar: Lika stor som tidigare, 0,00013. Vi kan se det genom att använda samma resonemang som tidigare.
Vi ska nu lämna matematiken för ett tag och fundera lite mer på den filosofiska frågan: Vad menar vi egentligen med en sannolikhet? Det finns här tre stora idéer kring sannolikheter: frekventalism, subjektiv sannolikhet och bayesianism.
Frekventalism, subjektiv sannolikhet och bayesianism
Vad menar vi när vi säger att sannolikheten är 50 procent för att ett mynt ska landa “krona upp”? En frekventalist skulle säga att det betyder att vi kommer att få krona i 50 procent av fallen i långa loppet, dvs. om vi kastar myntet om och om igen oändligt många gånger. Frekventalister tänker på sannolikheter som objektiva egenskaper hos utfallen i ett slumpmässigt försök. Det är objektiva egenskaper i den bemärkelsen att det inte spelar någon roll vad du eller jag tror eller har för erfarenheter från tidigare; sannolikheten för krona är fortfarande 50 procent. Och sannolikheterna gäller alltid utfallen i ett slumpmässigt försök, dvs. ett försök som kan upprepas om och om igen och där utfallet är okänt på förhand (såsom att dra kort ur en kortlek eller bollar ur en urna, singla slant, kasta tärning eller sampla individer ur en population). En frekventalist använder alltså sannolikheter för att kvantifiera hur pass troligt det är att det ena eller andra ska komma att inträffa då vi gör olika sorters mätningar eller observerar resultatet från ett försök.
Den frekventalistiska synen på sannolikheter dominerar inom vetenskapligt arbete. Men ibland blir idén om att upprepa ett försök “oändlig många gånger” rätt konstlad. Hur stor är sannolikheten för liv på Mars? Hur stor är sannolikheten för artificiell generell intelligens före år 2030? Hur stor är sannolikheten att Lee Harvey Oswald faktiskt mördade John F. Kennedy?
Här är sannolikheterna inte längre kopplade till utfallen i ett slumpmässigt försök, utan gäller istället hypoteser gällande vår omvärld. Sannolikheterna är nu ett sätt för oss att kvantifiera vår okunskap gällande sanningshalten i en viss hypotes.
Hur går den här kvantifieringen till? En möjlighet är att vi helt enkelt väljer den sannolikhet som bäst representerar styrkan i vår övertygelse. Detta kallas för subjektiv sannolikhet. Sannolikhetsbegreppet används rätt ofta på detta sätt i vardagligt tal och i expertutlåtanden, men kanske inte särskilt ofta inom vetenskapligt arbete.
Det finns också ett formellare sätt att kvantifiera vår okunskap. För en Bayesian bestäms sannolikheter utifrån Bayes teorem. Vi ser bäst vad det går ut på genom ett exempel.
Exempel. Gunbritt föddes antingen år 1940 eller år 1990. År 1940 fick 15 procent av flickor namnet Gunbritt. År 1990 var denna siffra 1 procent. Hur stor är sannolikheten att Gunbritt föddes år 1940? (Du kan här anta att lika många flickor föddes båda årtalen.) Svar: 0,9375.
Intuitionen: Anta att 100 flickor föddes år 1940 och 100 år 1990. I den första gruppen fick 15 namnet Gunbritt och i den andra fick 1 person namnet Gunbritt. Sannolikheten för att personen ifråga tillhör den första gruppen – alltså de som föddes 1940 – är då 15/16 = 0,9375.
Låt oss nu också se på “formellösningen”. Bayes teorem ges av:
\[P\left( A \middle| B \right) = \frac{P\left( B \middle| A \right)P(A)}{P(B)}\]
I detta exempel:
\[ P\!\left( \text{föddes 1940} \,\middle|\, \text{namngavs Gunbritt} \right) \]
\[ = \frac{P\!\left( \text{namngavs Gunbritt} \,\middle|\, \text{föddes 1940} \right)\, P(\text{föddes 1940})}{P(\text{namngavs Gunbritt})} = \frac{0,15 \times 0,5}{0,08} \]
\[ = 0,9375 \]
där \(P(\text{namngavs Gunbritt}) =\)
\[\begin{aligned} & P\!\left(\text{namngavs Gunbritt} \mid \text{född 1940}\right) \cdot P(\text{född 1940}) \\ +& P\!\left(\text{namngavs Gunbritt} \mid \text{född 1990}\right) \cdot P(\text{född 1990}) \\ =& 0.15 \times 0.5 + 0.01 \times 0.5 \\ =& 0.08 \end{aligned}\]Det kan vara värt att notera att Bayes teorem är korrekt för både frekventalister och Bayesianer; vi kan härleda teoremet från vår definition av betingade sannolikheter. Men för Bayesianer används teoremet för att bedöma hur pass sannolika olika hypoteser är (i detta exempel hypotesen om att personen ifråga föddes år 1940). Ur en frekventalistisk synvinkel så är Gunbritt född antingen år 1940 eller 1990. Om hon föddes år 1940 så är sannolikheten för att hon föddes år 1940 ett; om hon föddes år 1990 så är sannolikheten för att hon föddes år 1940 noll. Vår okunskap ändrar inte på den saken.
Så vad är då egentligen idén bakom Bayesianska sannolikheter? Jo, vi vill bedöma hur starkt förtroende vi har för en viss hypotes (“Personen är född år 1940”). Denna bedömning måste såklart bygga på någonting. Utan någon annan information så är sannolikheten 50 procent för att personen ifråga föddes år 1940. Denna sannolikhet kallas för vår prior. Men när vi också vet personens namn så uppdaterar vi vår kunskap och får en ny sannolikhet på 0,9375. Denna kallas för vår posterior. Ju lägre prior, desto starkare bevisbörda krävs det för att vi ska kunna hävda något med trovärdighet. Exempel: Anta att 10 procent av kvinnor föddes år 1940 och 90 procent år 1990. Då vore vår prior låg (0,1) och vår posterior skulle också vara relativt låg; sannolikheten för att Gunbritt föddes år 1940 skulle då vara 0,625 (testa att du kan bekräfta detta!). Men om vi hade starkare “bevis” – om vi till exempel dessutom visste att Gunbritt är en änka som tycker om att knyppla och äta fläskkotlett om söndagar – så ökar igen vår posterior.
\[ \underbrace{{\color{blue}{P\!\left( \text{föddes 1940} \,\middle|\, \text{namngavs Gunbritt} \right)}}}_{\text{posterior}} \]
\[ = \frac{P\!\left( \text{namngavs Gunbritt} \,\middle|\, \text{föddes 1940} \right)\, \overbrace{\color{red}{P(\text{föddes 1940})}}^{\text{prior}}}{P(\text{namngavs Gunbritt})} \]
Det kan vara värt att notera att man förstås inte behöver välja sida, vara antingen frekventalist eller bayesian. Vid vissa tillfällen kanske en idé passar bättre, ibland en annan. Den klassiska statistiska inferensen bygger dock på den frekventalistiska idéskolan. Därför säger vi till exempel att “µ ligger inom konfidensintervallet med 95-procentig säkerhet” (istället för sannolikhet). Ur en frekventalistisk synvinkel kommer µ nämligen alltid att antingen ha ett värde i intervallet eller inte – vår okunskap ändrar inte på den saken. Däremot kan vi legitimt säga att “sannolikheten är 95 procent att intervallets nedre gräns ligger under µ och att den övre ligger ovanför µ.” (Vi kan åtminstone säga detta ända fram tills dess att vi dragit samplet, om vi ska vara riktigt strikta.) Konfidensintervallets gränser bestäms nämligen som resultatet av ett slumpmässigt försök – sampling.
Sannolikhetsparadoxer
I många fall kommer vi ganska långt med vår intuition, men sen finns det också fall där intuitionen leder oss fel. Vi kallar detta för paradoxer. Vi ska se på några välkända sannolikhetsparadoxer här.
Exempel (Bertrands lådparadox). Vi har tre lådor. I den första lådan finns två guldmynt, i den andra lådan två silvermynt och i den tredje lådan finns ett guldmynt och ett silvermynt. Vi väljer nu slumpmässigt ut en låda och därefter ett mynt ur den lådan. Det visar sig att detta är ett guldmynt. Hur stor är sannolikheten att vi dragit myntet från den första lådan?
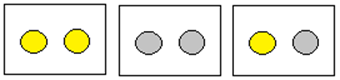
Många upplever att den sannolikheten borde vara 1/2, men den är 2/3. Vi vet alltså att vi fått ett av de tre guldmynten, och vart och ett är lika sannolikt, 1/3: Sannolikheten att vi fått något av de första två guldmynten är då 1/3+1/3 = 2/3.
Här är också ett sätt att tänka på saken. Numrera mynten ovan från 1 till 6, så att de tre guldmynten har nummer 1, 2 och 5. Anta nu att vi upprepar försöket ovan totalt 600 gånger, alltid enligt samma system (efter att vi dragit ett mynt lägger vi alltså tillbaka det på sin plats i lådan och drar nästa mynt tills vi gjort så 600 gånger). Då kan vi förvänta oss att få mynt nummer 1 i totalt 100 fall; mynt nummer 2 i 100 fall; … och mynt nummer 6 i 100 fall. (Varje mynt har ju samma sannolikhet att bli draget.) Av de 300 gånger då vi fått ett guldmynt så har det kommit från den första lådan i 200 fall och från den tredje lådan i 100 fall; sannolikheten för att ha dragit myntet från den första lådan är då 200/300 = 2/3.
Exempel (Monty Hall-problemet). I tv-serien Let’s Make a Deal ges den tävlande följande val. Bakom en av tre dörrar gömmer sig en åtråvärd vinst. Bakom de andra två dörrarna står en get. Den tävlande väljer på måfå en av dörrarna. Programledaren (som vet var vinsten finns) öppnar då en av de andra två dörrarna och ser då till att detta är en “getdörr”. Den tävlande får sedan möjligheten att byta dörr. Bör han eller hon göra det? Exempel: Anta att personen väljer dörr B och att programledaren öppnar dörr C. Den tävlande kan nu välja att stå fast vid sitt val (dörr B) eller byta till dörr A.
De allra flesta skulle nog säga att det inte spelar någon roll om den tävlande står fast vid sitt val (dörr B) eller byter till dörr A. För så måste det väl vara? Inte kan det löna sig att byta till dörr A? Den tävlande hade ju kunnat välja dörr A först. Skulle det då löna sig att byta till B?
Överraskande nog är svaret att det alltid lönar sig att byta! Om du byter så blir sannolikheten för vinst 2/3, annars 1/3. Låt oss se varför. Vi ska då göra följande tankeexperiment. 300 tävlande spelar detta spel, och alla dessa har som strategi att byta dörr efter att programledaren öppnat en getdörr. Anta att vinsten ligger bakom dörr A. 100 personer väljer dörr A; 100 personer väljer dörr B och 100 personer väljer dörr C. De som väljer dörr A kommer att byta till B eller C (beroende på vilken dörr programledaren öppnar) och förlorar sin vinst. De 100 som valde dörr B kommer att byta till dörr A (för programledaren kommer ju att öppna dörr C) och dessa kommer alltså att bli vinnare. De 100 som valde dörr C kommer att byta till dörr A med motsvarande motivering. Med den här strategin så vinner de tävlande alltså i 2 fall av 3. Det är bara då de råkat välja vinnardörren på första försöket som de förlorar, och det sker ju bara i en tredjedel av fallen.
Fortfarande inte övertygad? Här är ett annat sätt att se på saken. Vi kan då börja med att tänka oss att det fanns 100 dörrar från början. Du väljer en på måfå. Chansen är alltså 1/100 att du prickat vinstdörren. Chansen att vinsten finns bakom någon av de andra 99 dörrarna är 99/100. Anta att programledaren öppnar 98 av dessa och lämnar en oöppnad. Skulle du byta? Självklart! Programledaren har ju praktiskt taget pekat ut var vinsten hittas. Samma logik gäller i exemplet med tre dörrar.
Exempel (Födelsedagsproblemet). Hur många personer måste delta på en föreläsning för att sannolikheten ska vara minst 50 procent för att två (eller fler) av dem har samma födelsedag? De flesta skulle nog gissa att det kanske rör sig om närmare 100 personer eller fler. Svaret är förvånansvärt nog 23. Låt oss se varför.
Först kommer en student in i föreläsningssalen. Sannolikheten att denna är ensam om sin födelsedag är förstås 1 eller 365/365 (av 365 dagar på året så finns det 365 lediga). Sen kommer nästa person in i föreläsningssalen. Nu finns det 364 lediga dagar kvar. Sannolikheten att denna har en annan födelsedag än den första personen är då (364/365)*(365/365). Sen kommer den tredje personen in i föreläsningssalen. Sannolikheten att denna har en annan födelsedag än de andra två – givet att dessa har olika födelsedagar – är 363/365 och sannolikheten att alla tre har olika födelsedagar blir då (363/365)*(364/365)*(365/365). Exempel: Sannolikheten för att fem personer alla har olika födelsedagar blir:
(361/365)* (362/365)*(363/365)*(364/365)*(365/365)
Och sannolikheten för att alla fem inte har olika födelsedagar är då ett minus ovanstående:
1 – (361/365)* (362/365)*(363/365)*(364/365)*(365/365)
Genom att testa oss fram ser vi att det i förlängningen krävs 23 personer för att nå en sannolikhet på minst 50 procent.
Exempel (Törnrosa-problemet). Tänk dig följande experiment. En person försätts i koma på söndag. Försöksledaren singlar därefter slant. Om myntet landar “krona upp” så väcker man försökspersonen på måndag, intervjuar henne och försätter henne därefter i koma igen. Om myntet landar “klave upp” så väcker man henne på måndag, intervjuar henne, söver ner henne för att återigen väcka henne och intervjua henne på tisdag, efter vilket hon sövs ner igen. Oavsett om det blev krona eller klave så väcker man försökspersonen slutligen på onsdag och experimentet är då över.

När försökspersonen vaknar till en sådan intervju vet hon inte vilken dag det är eller om hon blivit intervjuad förut. Intervjun innehåller bara en fråga: Vad är sannolikheten att myntet landade “krona upp”? Fundera över vad du tycker hon borde svara!
Många hävdar här att 1/3 är rätt svar. Om vi tänker oss att detta experiment skulle utföras på många människor så skulle en tredjedel av alla intervjuer ske efter krona och två tredjedelar av alla intervjuer ske efter klave. Så sannolikheten att intervjun sker efter krona måste väl vara 1/3?!
Men flera hävdar också att 1/2 är rätt svar. Om vi tänker oss att detta experiment skulle utföras på många människor så skulle ju hälften ha fått krona och hälften klave. Så sannolikheten att hon hör till den första gruppen måste väl vara 1/2?!
Så vilket svar är rätt? 1/3 eller 1/2? Här är det märkliga … ingen vet. Det finns nämligen ingen konsensus. Flera filosofer har rivit sina hår över den här frågan, argumenterat och har publicerat sina lösningsförslag, men debatten fortsätter!
9.2 Sannolikhetsfördelningar
Vi gör ett slumpmässigt försök (såsom kastar en tärning, drar ett kort ur en kortlek eller en individ från en population). Hur ska vi beskriva sannolikheterna för de olika möjliga utfallen? Om utfallen kan beskrivas på en numerisk skala så kan vi använda oss av sannolikhetsfördelningar. Låt oss se några exempel på det.
Exempel. Vi kastar en symmetrisk tärning med sex möjliga utfall (1, 2, 3, 4, 5, 6). Sannolikhetsfördelningen ges då av:
P(X = 1) = P(X = 2) = … = P(X = 6) = 1/6
där X betecknar det okända utfallet (antalet prickar på tärningen). Här säger vi alltså att sannolikheten för att få en 1:a är lika stor som sannolikheten för en 2:a eller en 3:a och så vidare – varje sådan sannolikhet är 1/6. Figuren nedan beskriver samma sannolikhetsfördelning grafiskt. Vi skulle kalla det här för en likformig fördelning eftersom alla utfall är lika sannolika.
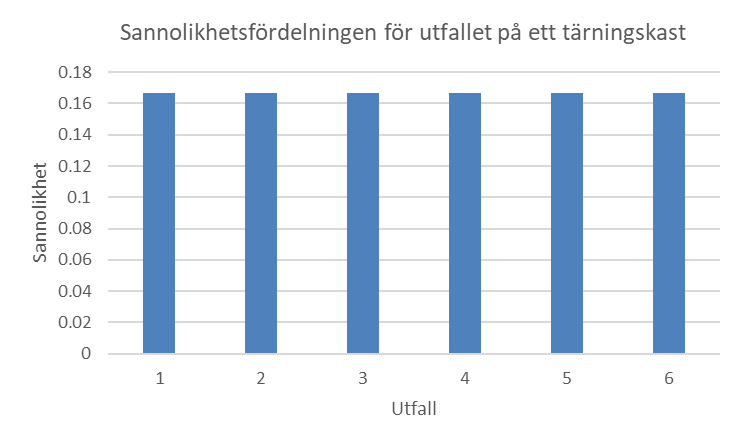
Den här sannolikhetsfördelningen är ett exempel på en diskret fördelning. Den är diskret eftersom vi bara kan få vissa distinkta utfall (1, 2, 3, …, 6) men inte, till exempel, värdet \(2\frac{1}{3}\).
Andra sannolikhetsfördelningar kan istället vara kontinuerliga så att variabeln ifråga kan anta vilket värde som helst inom något visst intervall. Exempel på kontinuerliga variabler är vikt, längd eller lön. (Om man ska vara helt korrekt så är lön egentligen en diskret variabel, för pengar mäts som finast i cent, så lönen kan strikt taget bara anta vissa distinkta värden. Men man brukar ändå behandla lönen som en kontinuerlig variabel, eftersom den är, så att säga, “nästan kontinuerlig”.)
Medan diskreta fördelningar illustreras genom stolpar, så illustreras kontinuerliga fördelningar med hjälp av kurvor.
Exempel. Låt X beteckna tiden det tar (i minuter) för en receptionist att betjäna en kund. X är en kontinuerlig variabel. Figuren nedan illustrerar att de flesta kunder har korta ärenden men vissa har komplicerade frågor som tar längre tid.
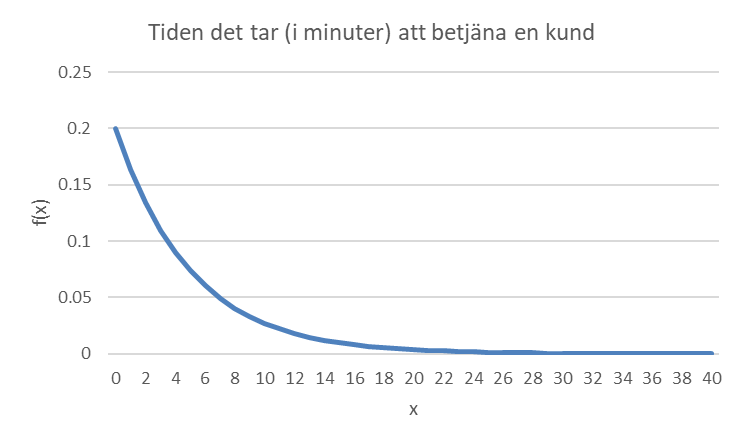
Kurvan ovan beskrivs av funktionen:
\[f(x) = 0,2e^{- 0,2x}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ då\ x \geq 0\]
\(f(x)\) betecknar höjden på kurvan vid olika värden på x. Exempel: Vid värdet 2 är höjden 0,134:
\[f(2) = 0,2e^{- 0,2 \times 2} \approx 0,134\]
Så på vilket sätt beskriver den här fördelningen sannolikheten för olika betjäningstider? Det kan här vara lockande att tänka att funktionen $ f(x) $beskriver just det – sannolikheten för en betjäningstid på x minuter, så att sannolikheten för en betjäningstid på 2 minuter skulle vara 13,4 procent. Men så är det alltså inte. När vi jobbar med kontinuerliga variabler så är sannolikheten för ett visst specifikt värde alltid 0. Sannolikhetsfördelningen, \(f(x)\), speglar istället sannolikheten för att få ett utfall i närheten av ett visst värde. Från figuren ovan ser vi till exempel att sannolikheten för en betjäningstid nära 2 minuter är betydligt större än sannolikheten för en betjäningstid nära 10 minuter. Om vi matar in värdet 2 i funktionen ovan så ser vi att höjden där är 0,134; matar vi in värdet 10 så ser vi att höjden där är 0,027. Sannolikheten för en betjäningstid nära 2 minuter är alltså ca fem gånger större än sannolikheten för en betjäningstid nära 10 minuter.
Så varför är sannolikheten noll för en betjäningstid på exakt 2 minuter? Tänk så här: Sannolikheten för en betjäningstid någonstans mellan 2 och 3 minuter är 12 procent i detta exempel. Sannolikheten för en betjäningstid någonstans mellan 2 och 2,1 minuter är då ungefär en tiondel av det (1,2 procent) och sannolikheten för en betjäningstid någonstans mellan 2 och 2,01 minuter är ungefär en tiondel av det (0,12 procent), osv. Om vi på detta sätt fortsätter att minska på intervallets bredd så ser vi att sannolikheten går mot noll då intervallets bredd går mot noll. Eller med andra ord: Sannolikheten är noll för en betjäningstid med det exakta värdet 2,00000… (följt av oändligt många nollor).1
Om \(f(x)\) inte beskriver sannolikheten för en betjäningstid på x minuter – vad beskriver kurvan i så fall? Jo, arean under fördelningen och mellan två värden är sannolikheten för att få ett värde i det intervallet. Hela arean under fördelningen är 1. Exempel: Arean mellan 2 och 10 är ungefär 0,54 (utmålad i gult nedan). Sannolikheten för en betjäningstid någonstans i det intervallet är alltså 54 procent.
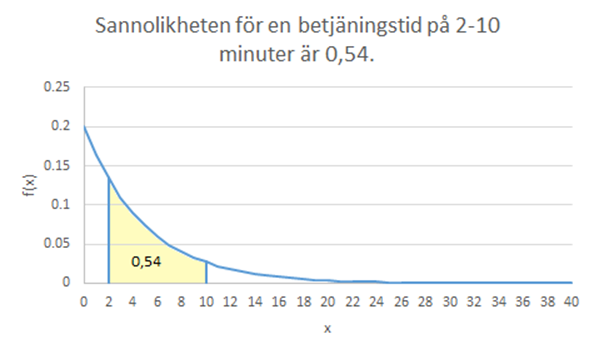
Hur kan vi räkna ut hur stor den gula arena är? Jo, vi kan här utnyttja den kumulativa fördelningsfunktionen som beskriver sannolikheten för att få ett värde på x eller mindre. I detta fall ges den kumulativa fördelningsfunktionen av:
\[P(X \leq x) = F(x) = 1 - e^{- 0,2x}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ då\ x \geq 0\]
\(P(X \leq x)\) läses som “sannolikheten för att X (=betjäningstiden) ska få ett värde på x eller mindre.” Stora X betecknar alltså själva variabeln (betjäningstiden) och lilla x betecknar ett konkret värde på den variabeln. Denna sannolikhet kan också betecknas med F(x). Nedan ges den kumulativa fördelningsfunktionen grafiskt:
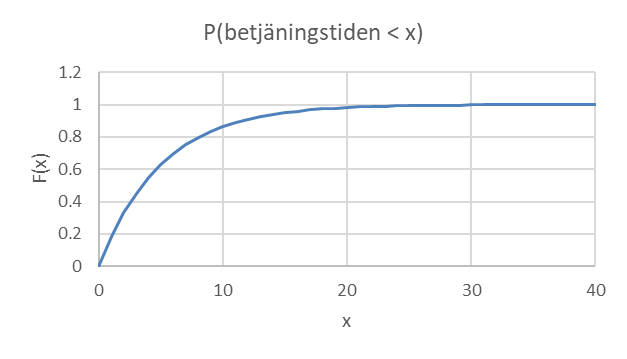
Sannolikheten för en betjäningstid på 10 minuter eller mindre ges då av:
\[P(X \leq 10) = F(10) = 1 - e^{- 0.2 \times 10} \approx 0,865\]
Och sannolikheten för en betjäningstid på 2 minuter eller mindre ges av:
\[P(X \leq 2) = F(2) = 1 - e^{- 0.2 \times 2} \approx 0,330\]
Sannolikheten för en betjäningstid någonstans i intervallet 2-10 minuter ges av:
\[P(2 \leq X \leq 10) = P(X \leq 10) - P(X \leq 2) = 0,865 - 0,330 = 0,535\]
Exempel forts. Anta att du har en kund framför dig i kön. Hur stor är sannolikheten att du måste vänta minst 10 minuter? Svar: 13,5 procent:
\[P(X \geq 10) = 1 - P(X \leq 10) = 1 - 0,865 = 0,135\]
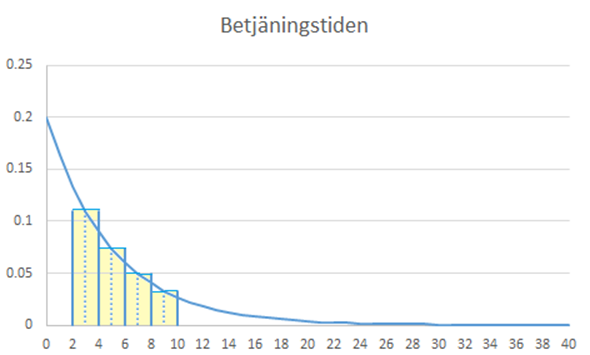
Innan vi går vidare ska vi fundera lite på varifrån den kumulativa fördelningsfunktionen egentligen kom. För att se detta så ska vi börja med att approximera sannolikheten för att betjäningstiden ligger någonstans i intervallet 2-10 minuter. I figuren nedan har vi delat upp denna area i fyra rektanglar. Vi kan då beräkna arean för varje rektangel och summera ihop. Exempel: Den första rektangeln har en höjd på f(3) ≈ 0,11 och en bredd på 2 enheter. Arean blir alltså 0,22 enheter. På motsvarande sätt kan vi beräkna arean för de andra tre rektanglarna. Summan blir 0,531 vilket ligger relativt nära sanningen (0,535).
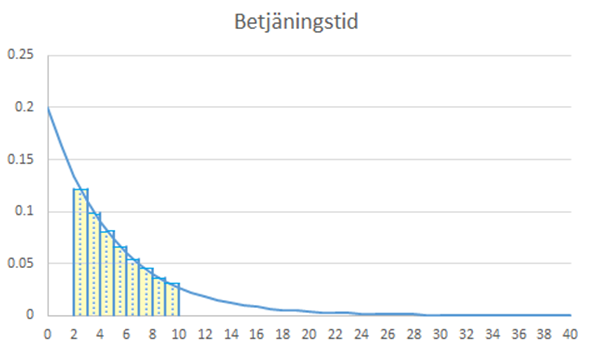
En bättre approximation kan vi få genom att dela in området i ännu fler rektanglar. I figuren nedan har jag använt åtta. Summan av dessa är 0,534 vilket ligger ännu närmare sanningen (0,535).
När vi integrerar över ett område (säg från x=2 till x=10) så är det som om vi skulle dela in området i oändligt många dylika rektanglar och “summera ihop” alla dessa. På så vis får vi den exakta sannolikheten. Hur detta funkar rent tekniskt är en lite längre historia, men med datorns hjälp är det ofta enkelt gjort. Här har jag använt sidan Symbolab för att utföra integreringen.
\[P(2 \leq x \leq 10) = \int_{2}^{10}{0,2e^{- 0.2x}}\ dx = 0,53498\ldots\]
där ∫ är integraltecknet; här integrerar vi alltså från värdet 2 och upp till värdet 10. \(0,2e^{- 0.2x}\) beskriver sannolikhetsfördelningens funktion och symbolen dx visar att vi integrerar med avseende på x.
När vi på detta vis integrerar från det minsta möjliga värdet (här 0) och upp till värdet x så får vi den kumulativa fördelningsfunktionen:
\[F(x) = \int_{0}^{x}{0,2e^{- 0.2x}}\ dx = 1 - e^{- 0.2x}\]
som vi sen kan utnyttja för att beräkna olika sannolikheter.
Väntevärdet och variansen i en sannolikhetsfördelning
Precis som vi tidigare beräknat olika mått – såsom medelvärdet och variansen – för en empirisk fördelning så kan vi använda samma mått för att karaktärisera sannolikhetsfördelningar. Medelvärdet i en sannolikhetsfördelning kallas också för väntevärdet, det förväntade värdet eller populationsmedelvärdet.
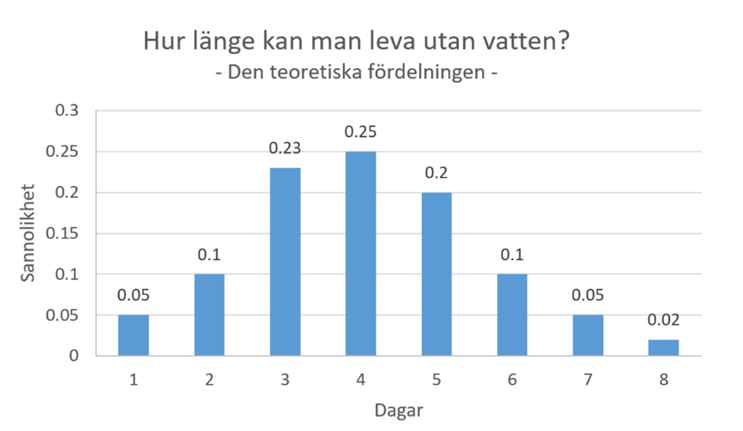
Exempel. Hur länge kan man leva utan vatten? Sannolikhetsfördelningen nedan beskriver detta. Typiskt sett klarar man sig alltså 3 till 5 dygn.
Vi ska nu tänka oss att 100 olycksaliga själar strandar på en öde ö utan tillgång till vatten (vi kan betrakta dessa 100 personer som ett slumpmässigt sampel från populationen ovan). Figuren nedan visar den empiriska fördelningen, dvs. samplets fördelning.
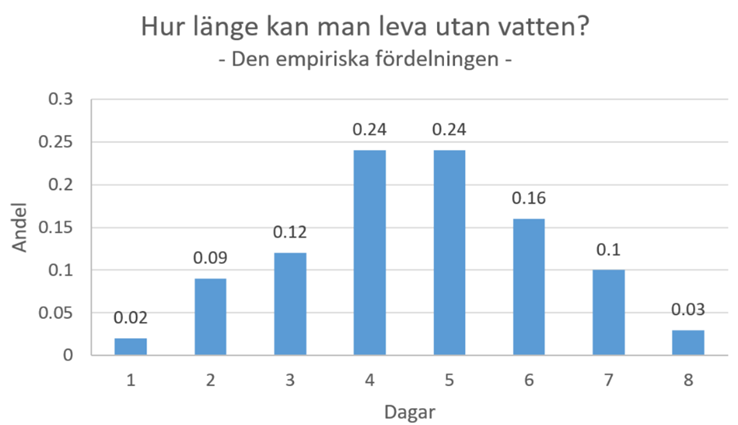
Vi ser att den empiriska fördelningen liknar den teoretiska, precis som den borde. Men den sammanfaller förstås inte perfekt med den teoretiska fördelningen, ty slumpen gör också sitt.
Hur länge har personerna i samplet i snitt hållit ut? Jo, ett sätt att beräkna stickprovsmedelvärdet är att vikta varje värde med sin andel och summera ihop:
\[ \overline{x} = {\color{blue}{1}} \times 0,02 + {\color{blue}{2}} \times 0,09 + {\color{blue}{3}} \times 0,12 + {\color{blue}{4}} \times 0,24 + {\color{blue}{5}} \times 0,24 + {\color{blue}{6}} \times 0,16 + {\color{blue}{7}} \times 0,10 + {\color{blue}{8}} \times 0,03 = 4,62 \]
I snitt höll personerna alltså ut 4,62 dagar. Men den här siffran är förstås bara ett estimat och gäller just dessa 100 personer. För att veta sanningen så ska vi ännu beräkna populationsmedelvärdet, µ. För att veta sanningen så ska vi ännu beräkna populationsmedelvärdet, µ. Vi får det på motsvarande sätt, bara att vi nu viktar varje möjligt utfall med sin sannolikhet och summerar ihop:
\[ \mu = {\color{blue}{1}} \times 0,05 + {\color{blue}{2}} \times 0,1 + {\color{blue}{3}} \times 0,23 + {\color{blue}{4}} \times 0,25 + {\color{blue}{5}} \times 0,2 + {\color{blue}{6}} \times 0,1 + {\color{blue}{7}} \times 0,05 + {\color{blue}{8}} \times 0,02 = 4,05 \]
Stickprovsmedelvärdet råkade alltså denna gång bli högre än populationsmedelvärdet, men det hade lika bra kunna gå andra vägen. Då sampelstorleken ökar så kommer dock den empiriska fördelningen att allt mer börja likna den teoretiska och \(\overline{x}\) närmar sig µ. Detta är ett exempel på det som kallas för de stora talens lag. De stora talens lag är en viktig sats inom statistiken. Den säger nämligen att vår empiriska fördelning kan komma hur nära den teoretiska som helst, bara vi samlar in tillräckligt mycket data. Detta gäller åtminstone om samplet är slumpmässigt draget. Låt oss göra ett tankeexperiment som beskriver det här konceptet: Tänk dig att vi kastar tärning. Vad är väntevärdet för utfallet på ett kast? Jo, 3,5:
\[\mu = 1 \times \frac{1}{6} + 2 \times \frac{1}{6} + 3 \times \frac{1}{6} + 4 \times \frac{1}{6} + 5 \times \frac{1}{6} + 6 \times \frac{1}{6} = 3,5\]
Med hjälp av en dator kan vi “kasta tärning” upprepade gånger. Här har jag gjort det 10 gånger:
4, 4, 6, 5, 6, 3, 4, 4, 4, 6
Medelvärdet blev 4,6. Men vi stannar inte här. Vi fortsätter nu att kasta tärningen:
Efter 100 kast är medelvärdet 3,83.
Efter 1000 kast är medelvärdet 3,532.
Efter 10 000 kast är medelvärdet 3,533.
Efter 100 000 kast är medelvärdet 3,498.
Figuren nedan beskriver hur medelvärdet utvecklades med antalet kast.
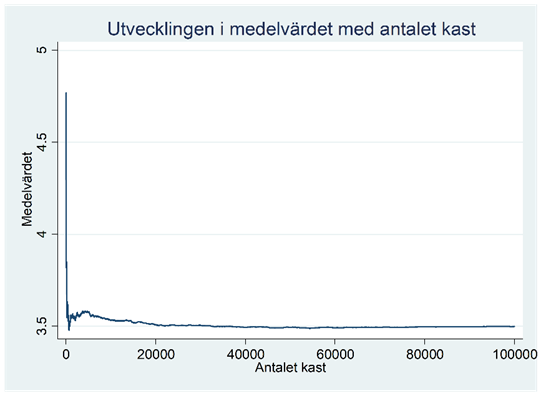
Så här kunde vi fortsätta att kasta tärningen och räkna ut medelvärdet utifrån ett allt större antal kast. Vilket medelvärde skulle vi få om vi lät antalet kast gå mot oändligheten? Jo, 3,5.
Ovan använde vi µ som beteckning för väntevärdet. En annan lika vanlig beteckning är denna:
\[\mu = E(X)\]
där E:et är kort för “expectancy”, dvs. förväntat värde eller väntevärde. E(X) är alltså väntevärdet för variabeln X.
Populationsvariansen är det förväntade kvadrerade avståndet mellan ett möjligt utfall och populationsmedelvärdet:
\[\sigma^{2} = E\left\lbrack {(X - \mu)}^{2} \right\rbrack\]
Exempel forts. Om du bara överlevde en dag utan vatten så ligger du 3,05 dagar under populationsmedelvärdet eller 9,3025 dagar i kvadrat. Vi tar alltså varje sådant kvadrerat avstånd, viktar det med sin sannolikhet och summerar ihop:
\[\begin{aligned} \sigma^{2} &= {\color{blue}{9,3025}} \times 0,05 + {\color{blue}{4,2025}} \times 0,1 + {\color{blue}{1,1025}} \times 0,23 + {\color{blue}{0,0025}} \times 0,25 \\ &\quad + {\color{blue}{0,9025}} \times 0,2 + {\color{blue}{3,8025}} \times 0,1 + {\color{blue}{8,7025}} \times 0,05 + {\color{blue}{15,6025}} \times 0,02 \\ &= 2,4475 \end{aligned}\]Standardavvikelsen, σ, fås som tidigare genom att ta kvadratroten ur variansen.
Följande formel för variansen ger samma resultat (men kanske lite snabbare när man räknar manuellt):
\[\sigma^{2} = E\left\lbrack {(X - \mu)}^{2} \right\rbrack = E\left( X^{2} \right) - \mu^{2}\]
Låt oss testa. Vi börjar då med \(E\left( X^{2} \right)\). Här ska vi alltså ta varje kvadrerat värde, vikta det med sin sannolikhet och summera ihop:
\[\begin{aligned} E\!\left( X^{2} \right) &= {\color{blue}{1^{2}}} \times 0,05 + {\color{blue}{2^{2}}} \times 0,1 + {\color{blue}{3^{2}}} \times 0,23 + {\color{blue}{4^{2}}} \times 0,25 \\ &\quad + {\color{blue}{5^{2}}} \times 0,2 + {\color{blue}{6^{2}}} \times 0,1 + {\color{blue}{7^{2}}} \times 0,05 + {\color{blue}{8^{2}}} \times 0,02 \\ &= 18,85 \end{aligned}\]Variansen fås sen genom att dra ifrån \(\mu^{2}\):
\[ \sigma^{2} = \underbrace{18,85}_{E\!\left(X^{2}\right)} - \underbrace{(4,05)^{2}}_{\mu^{2}} = 2,4475 \]
Ovan använde vi \(\sigma^{2}\) som beteckning för variansen. Två andra lika vanlig beteckningar är dessa:
\[\sigma^{2} = Var(X) = V(X)\]
De här beräkningarna för väntevärdet och variansen fungerar dock bara för diskreta fördelningar. Men principen är densamma också för kontinuerliga fördelningar. För diskreta fördelningar bestäms populationsmedelvärdet som:
\[\mu = \sum_{}^{}{x_{i} \times p_{i}}\]
där xi betecknar ett möjligt utfall och pi betecknar sannolikheten för det utfallet. Med en kontinuerlig fördelning fås populationsmedelvärdet som:
\[\mu = \int_{- \infty}^{\infty}{x \times f(x)dx}\]
Istället för att summera över \(x \times p\) integrerar vi över \(x \times f(x)\).
Variansen i en diskret respektive kontinuerlig fördelning ges på motsvarande sätt av:
\[\sigma^{2} = \sum_{}^{}{\left( x_{i} - \mu \right)^{2} \times p_{i}}\]
\[\sigma^{2} = \int_{- \infty}^{\infty}{(x - \mu)^{2} \times f(x)dx}\]
Vi har nu sett några exempel på sannolikhetsfördelningar. Vi ska fortsätta med att se på två extra kända fördelningar som man ofta har nytta av inom statistisk inferens: binomialfördelningen och normalfördelningen.
Binomialfördelningen
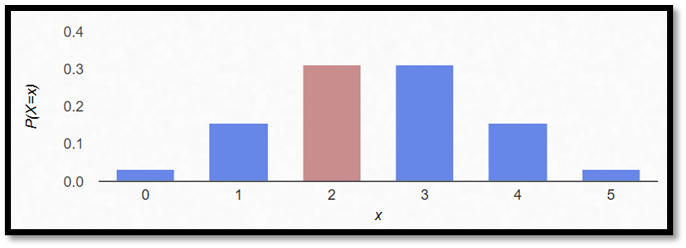
Exempel. Vi singlar slant fem gånger. Hur stor är sannolikheten för att få exakt två stycken krona?
För att beräkna denna sannolikhet så kan vi utnyttja binomialfördelningen. Alltid när vi vill beräkna sannolikheten för att få “k gynnsamma utfall bland n stycken identiska och oberoende försök” så blir binomialfördelningen aktuell. Vi får då sannolikheten för k stycken gynnsamma utfall som:
\[P(X = k) = \begin{pmatrix} n \\ k \\ \end{pmatrix}p^{k}{(1 - p)}^{n - k}\]
där X är det vi mäter (här “antalet krona”); k är antalet gynnsamma utfall (här 2); n är antalet försök (här 5) och p är sannolikheten för ett gynnsamt utfall (här 0,5).
\(\begin{pmatrix} n \\ k \\ \end{pmatrix}\) uttalas “n över k” och är antalet sätt på vilka vi kan få k gynnsamma utfall bland n försök. Exempel: Ett sätt att få 2 krona på 5 försök är att vi först får två stycken krona och därefter tre klave. Men totalt finns det 10 sådana sätt:

“n över k” beräknas som:
\[\begin{pmatrix} n \\ k \\ \end{pmatrix} = \frac{n!}{k!(n - k)!}\]
där \(n!\) uttalas “n fakultet”. Det är kort för produkten:
\(n! = \ n \times (n - 1) \times (n - 2) \times \ldots \times 1\).
5! är alltså lika med 5*4*3*2*1 = 120. Och 0! = 1. I vårt fall finns det alltså totalt 10 sätt att ordna två stycken krona bland fem slantsinglingar:
\[\begin{pmatrix} 5 \\ 2 \\ \end{pmatrix} = \frac{5!}{2!(5 - 2)!} = 10\]
Den sökta sannolikheten ges då av:
\[P(X = 2) = \begin{pmatrix} 5 \\ 2 \\ \end{pmatrix}{0,5}^{2}{(1 - 0,5)}^{5 - 2} = 0,3125\]
Figuren nedan beskriver sannolikheten för allt mellan 0 och 5 stycken krona:
Exempel. Ett flygplan har 100 platser. Sannolikheten för att en person som bokat en biljett också dyker upp är 85 procent. Anta att man sålt totalt 110 biljetter. Hur stor är sannolikheten att flyget blir överfullt, dvs. att 101 personer eller fler dyker upp? Den sannolikheten ges av:
\[P(X \geq 101) = P(X = 101) + P(X = 102) + P(X = 103) + \ldots + P(X = 110)\]
\[= \begin{pmatrix} 110 \\ 101 \\ \end{pmatrix}{0,85}^{101}(1 - 0,85)^{110 - 101} + \begin{pmatrix} 110 \\ 102 \\ \end{pmatrix}{0,85}^{102}(1 - 0,85)^{110 - 102}\]
\[+ \begin{pmatrix} 110 \\ 103 \\ \end{pmatrix}{0,85}^{103}(1 - 0,85)^{110 - 103} + \ldots + \begin{pmatrix} 110 \\ 110 \\ \end{pmatrix}{0,85}^{110}(1 - 0,85)^{110 - 110}\]
Den här beräkningen görs snabbast med hjälp av en kalkylator, såsom följande:
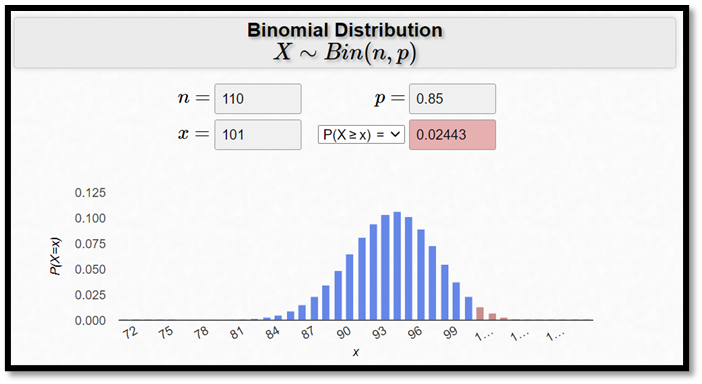
Den sökta sannolikheten är alltså 0,02443.
Det kan vara värt att notera att det här svaret är en approximation som bygger på antagandet om att försöken är oberoende, dvs. sannolikheten för att en passagerare dyker upp är oberoende av om en annan gör det eller inte. Det här är kanske inte helt realistiskt i praktiken; personer flyger ju ofta tillsammans med familj eller vänner och då kommer vanligtvis alla eller ingen från en sådan grupp.
Binomialfördelningen är ett exempel på en diskret sannolikhetsfördelning. Vi kan beräkna väntevärdet och variansen i den fördelningen enligt:
\[E(X) = np\ \ \ \ \ \ Var(X) = np(1 - p)\]
I detta exempel förväntas alltså 93,5 personer dyka upp:
\[E(X) = np = 110 \times 0,85 = 93,5\]
Vi kallar n och p för binomialfördelningens parametrar; genom att variera dessa får vi nämligen olika binomialfördelningar. Dessa två värden tillsammans bestämmer exakt vilken binomialfördelning det är frågan om. Om vi vill säga att en viss variabel (såsom antalet passagerare) är binomialfördelad med n = 115 och p = 0,85 så kan vi uttrycka det så här:
\[Antal\ passagerare\ \sim\ Bin({\color{red}{115}};{\color{blue}{0,85}})\]
Normalfördelningen
Den allra mest kända kontinuerliga sannolikhetsfördelningen är normalfördelningen. Figuren nedan visar hur en normalfördelning ser ut.
där kurvans ekvation ges av:
\[f(x) = \frac{1}{\sigma\sqrt{2\pi}}e^{\frac{- 0,5(x - \mu)^{2}}{\sigma^{2}}}\]
x är det vi mäter, såsom längd, blodtryck eller IQ. µ är fördelningens medelvärde och σ är standardavvikelsen. Vi kallar µ och σ för normalfördelningens parametrar. Det betyder att dessa två tillsammans bestämmer vilken normalfördelning det är frågan om. Vi kan alltså få olika normalfördelningar genom att variera µ och σ.
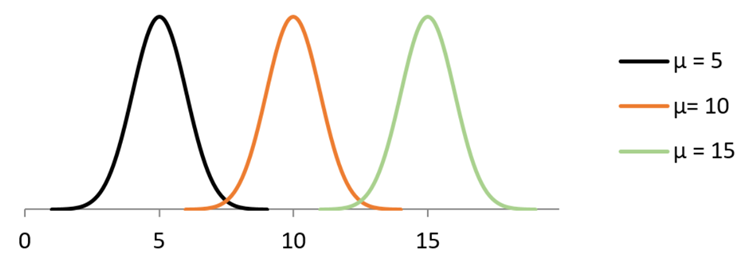
Genom att ändra µ så flyttar vi normalfördelningen längs med tallinjen:
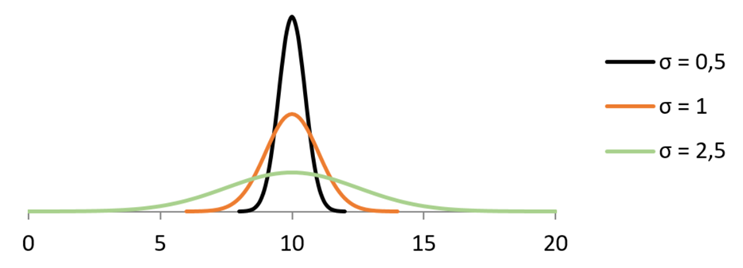
Standardavvikelsen, σ, bestämmer fördelningens spridning:
Om vi vill säga att en viss variabel, X, är normalfördelad med väntevärde µ och standardavvikelsen \(\sigma\) så kan vi kortfattat skriva:
\[X \sim N(\mu,\ \sigma)\]
Exempel. Här säger vi att intelligenskvoten är normalfördelad med medelvärde 100 och standardavvikelsen 15: IQ \(\sim N(100,\ 15)\)
Den här normalfördelningen illustreras nedan.
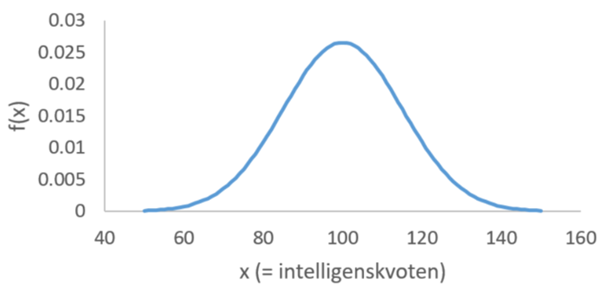
Vi ska ännu nämna två centrala egenskaper gällande normalfördelningen: 1) Den är symmetrisk runt sitt medelvärde. I vårt exempel gäller alltså att sannolikheten för en intelligenskvot på 80 eller lägre är lika stor som sannolikheten för en intelligenskvot på 120 eller högre. 2) 95-100-regeln: Ungefär 95 procent av fallen ryms inom +/- 2 standardavvikelser från medelvärdet, och närmare 100 procent inom +/- 3 standardavvikelser från medelvärdet. I vårt exempel gäller alltså att ca 95 procent har en intelligenskvot någonstans mellan 70 och 130 poäng. (Standardavvikelsen var ju 15!)
95-100-regeln är praktisk då vi vill få en snabb bild av var den stora massan faller. Men den tillåter oss inte att beräkna sannolikheter för andra intervall. Hur stor är till exempel sannolikheten för att en slumpmässigt utvald individ ska ha en intelligenskvot på 120 eller högre? Eller, säg, 85 eller lägre?
Tidigare såg vi att vi kan använda den kumulativa fördelningsfunktionen för att beräkna dylika sannolikheter. Men här stöter vi på ett problem – normalfördelningens kumulativa fördelningsfunktion kan nämligen inte uttryckas genom en sluten funktion (= en funktion som består av ett visst antal konstanter, variabler och välkända operatörer såsom plus, minus, gånger och division). För att beräkna sannolikheter utifrån normalfördelningen använder vi istället uppgjorda tabeller eller kalkylatorer. Vi kommer då att ha nytta av standardiserade skalor, så låt oss först se vad det betyder.
Exempel forts. Anta att du har en intelligenskvot på 115 poäng. Då ligger du exakt en standardavvikelse ovanför medelvärdet; medelvärdet var ju 100 och standardavvikelsen 15. Vi säger då att du har en intelligenskvot på x = 115 poäng men en standardiserad intelligenskvot på z = 1 standardavvikelse. När vi på det här sättet uttrycker någonting i standardavvikelser från medelvärdet så använder vi en standardiserad skala. Här är ytterligare ett par exempel:
Om du har en intelligenskvot på 130 poäng så ligger du 2 standardavvikelser ovanför medelvärdet: z = 2. Och om du har en intelligenskvot på 85 poäng så ligger du 1 standardavvikelse under medelvärdet: z = -1. Figuren nedan illustrerar dessa två skalor i samma figur, där de standardiserade värdena ges i rött.
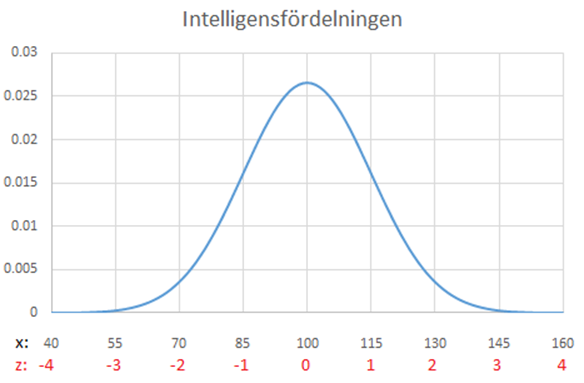
Vi kan räkna ut det standardiserade värdet (z) som:
\[z = \frac{x - \mu}{\sigma}\]
Exempel forts. Hur stor är sannolikheten för en intelligenskvot på 94 poäng eller mindre? Om man har en intelligenskvot på 94 poäng så ligger man 6 poäng under medelvärdet, och 6 poäng är 40 procent av en standardavvikelse: 6/15 = 0,4. Eller med andra ord: Man ligger då 0,4 standardavvikelser under medelvärdet: z = -0,4.
\[z = \frac{x - \mu}{\sigma} = \frac{94 - 100}{15} = - 0,4\]
Sannolikheten för en intelligenskvot på 94 eller lägre är alltså lika stor som sannolikheten för att ligga 0,4 standardavvikelser under medelvärdet eller lägre:
P(IQ ≤ 94) = P(Z ≤ -0,4)
Hur stor är denna sannolikhet? Om du har beräknat normalfördelade sannolikheter under skoltiden så använde du dig kanske av den tabell som låg längst bak i MAOLS. Här ser du ett utdrag ur en sådan tabell.
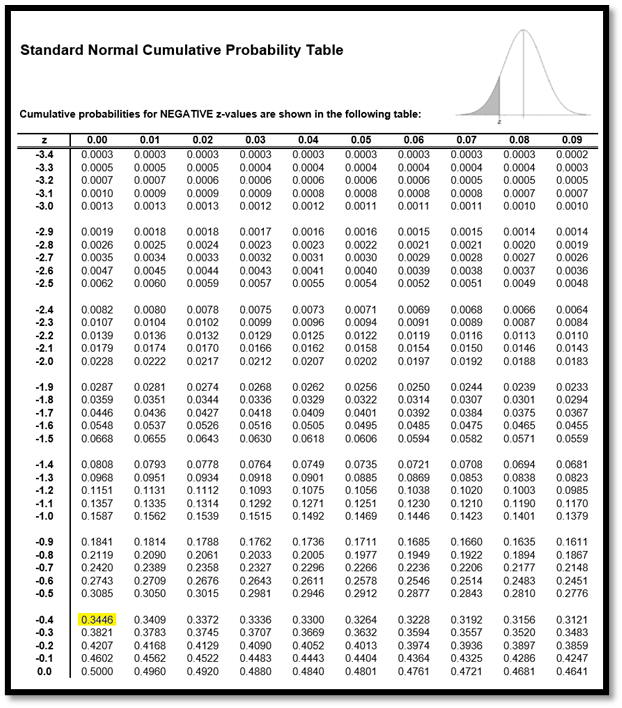
Här letar jag upp värdet -0,40. Värdet -0,4 hittas i den första kolumnen och den andra decimalen (-0,40) hittas på första raden. Den sökta sannolikheten är 0,3446.
Om du redan råkar sitta vid en dator så är det kanske lite smidigare att låta den sköta jobbet. Det finns många online-kalkylatorer som kan användas, såsom denna:
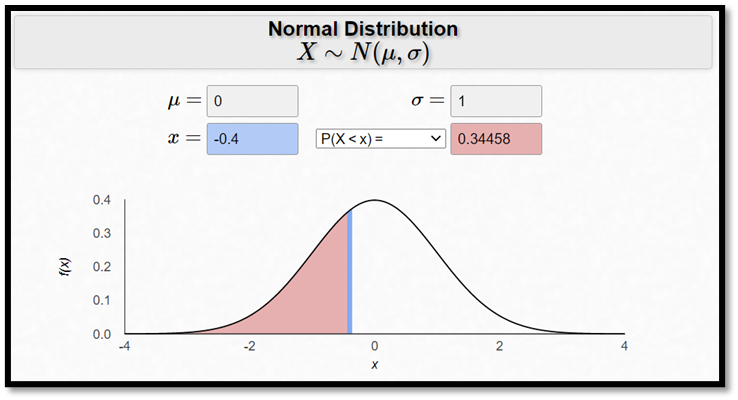
Exempel forts. Hur stor är då sannolikheten för en intelligenskvot på 106 eller större? Jo, den är också 0,3446. Normalfördelningen är ju symmetrisk kring medelvärdet. Sannolikheten för en intelligenskvot på 94 eller mindre är alltså exakt lika stor som sannolikheten för en intelligenskvot på 106 eller större.
9.3 Samplingfördelningen för ett stickprovsmedelvärde
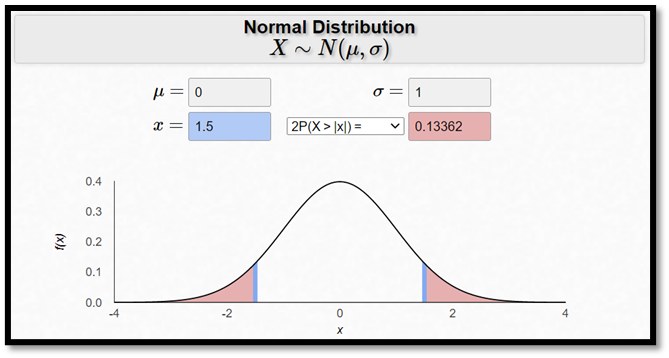
Exempel forts. Anta som tidigare att intelligenskvoten är normalfördelad med medelvärde 100 och standardavvikelsen 15. Sannolikheten för att en slumpmässigt utvald individ ska ha en intelligenskvot på 110 eller högre är då ungefär 25 procent.
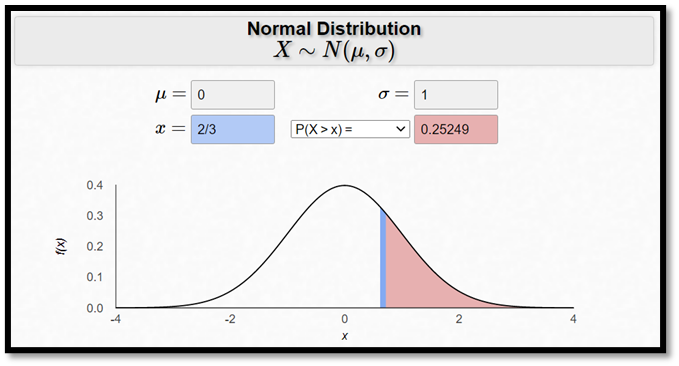
Om du ligger 10 poäng över medelvärdet så ligger du 10/15 = 2/3 av en standardavvikelse ovanför medelvärdet. Du har alltså en standardiserad intelligenskvot på 2/3. Figuren ovan visar att sannolikheten för att ligga minst 2/3 av en standardavvikelse ovanför medelvärdet är ca 25 procent.
Exempel forts. Anta nu att vi slumpmässigt väljer ut två individer. Hur stor är sannolikheten att dessa två i snitt har en intelligenskvot på minst 110?
\[P(\overline{X} \geq 110)\]
Det här kan förstås hända på många olika sätt. Om den första råkar ha en intelligenskvot på 100 och den andra 130 så blir snittet över 110. Eller om den första råkar ha en intelligenskvot på 150 och den andra 80 så blir också snittet över 110. Eller så kanske båda råkar har en intelligenskvot på 110+.
Med hjälp av en dator kan vi lösa problemet genom att testa oss fram. Jag väljer slumpmässigt ut två individer från populationen. Det visar sig att den första har en intelligenskvot på 91 och den andra 100. Medelvärdet är alltså 95,5. Och så upprepar jag detta en andra gång. Nu fick den första en intelligenskvot på 103 och den andra 97. Medelvärdet landade på 100 jämnt. Och jag slutar inte heller här. Jag samplar återigen två personer och denna gång landade medelvärdet på 103. Med datorns hjälp kan detta försök göras om och om igen nästan utan ände. Här har jag upprepat försöket totalt 100 000 gånger och fått 100 000 medelvärden. Tabellen nedan visar ett utdrag av resultatet.
Figuren nedan beskriver fördelningen för alla dessa 100 000 medelvärden.
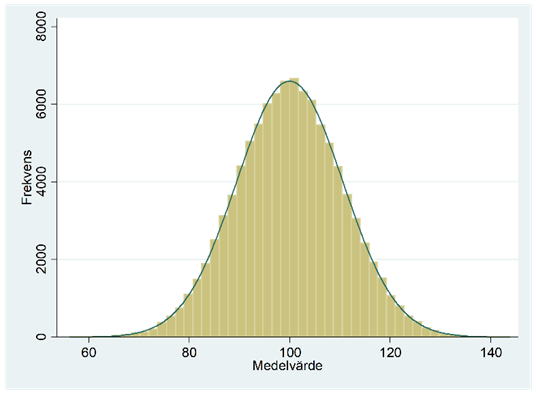
Fördelningen ovan är ett exempel på en samplingfördelning för ett stickprovsmedelvärde. En sådan fördelning är alltså en sannolikhetsfördelning som beskriver fördelningen för olika stickprovsmedelvärden då vi drar upprepade sampel, alltid av någon viss storlek (här n = 2). Om vi ska vara korrekta så vore detta samplingfördelningen först när vi låter antalet sampel gå mot oändligheten, men 100 000 är tillräckligt nära för att ge oss en bra bild av den egentliga samplingfördelningen.
Så vad kan vi säga om denna fördelning? För det första: Vad är väntevärdet och standardavvikelsen i den här fördelningen? Baserat på dessa 100 000 sampel så har medelvärdet hamnat på 100,0 och standardavvikelsen på 10,6. Teoretiskt sett kan vi beräkna väntevärdet och standardavvikelsen i samplingfördelningen för ett stickprovsmedelvärde som:
\[\mu_{\overline{x}} = \mu\]
och
\[\sigma_{\overline{x}} = \frac{\sigma}{\sqrt{n}}\]
där \(\mu\) och \(\sigma\) är medelvärdet och standardavvikelsen i populationen, och där n är antalet observationer (här 2). I vårt exempel har vi alltså att:
\[\mu_{\overline{x}} = \mu = 100\]
och
\[\sigma_{\overline{x}} = \frac{\sigma}{\sqrt{n}} = \frac{15}{\sqrt{2}} = 10,6066\ldots\]
Vi ser alltså att väntevärdet i samplingfördelningen, \(\mu_{\overline{x}}\), är lika stort som i populationen. Eller med andra ord: När vi drar ett sampel så kommer stickprovsmedelvärdet ibland ligga för högt, ibland för lågt, men i genomsnitt i långa loppet blir det rätt.
Vi ser också att standardavvikelsen i samplingfördelningen (10,6) är lägre än den i populationen (15). Det här innebär alltså att sannolikheten för att en person har en intelligenskvot på 110+ är större än sannolikheten för att två personer har det i snitt. Och om vi samplade tusentals eller miljontals individer så vore det ytterst osannolikt att dessa snittade 110+. Varje gång sampelstorleken blir fyra gånger större så halveras standardavvikelsen i samplingfördelningen.
Vilken fördelningsform följer då samplingfördelningen för stickprovsmedelvärdet? Jo, då våra individer är dragna från en normalfördelning så kommer också stickprovsmedelvärdet att följa en normalfördelning, vilket figuren ovan också visade.
Så hur stor är då sannolikheten för att få ett stickprovsmedelvärde på 110+ då vi slumpmässigt samplar två personer? Jo, ca 0,17:
\[P\left( \overline{X} \geq 110 \right) \approx P(Z \geq 0,94) \approx 0,17\]
där
\[z = \frac{\overline{x} - \mu}{\sigma_{\overline{x}}} = \frac{110 - 100}{15/\sqrt{2}} \approx 0,94\]
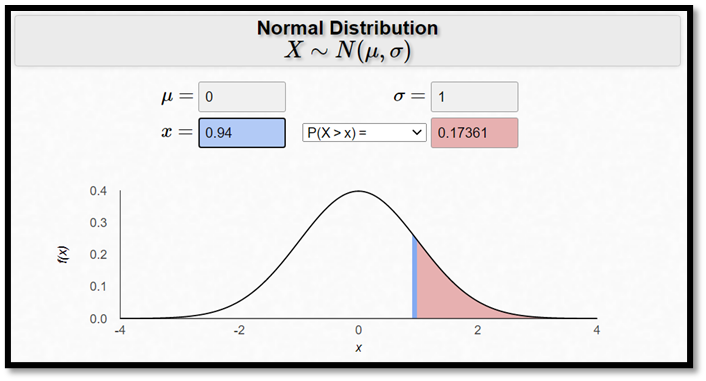
Det här stämmer väl överens med våra 100 000 sampel, där 16,7 procent resulterade i ett stickprovsmedelvärde på 110+.
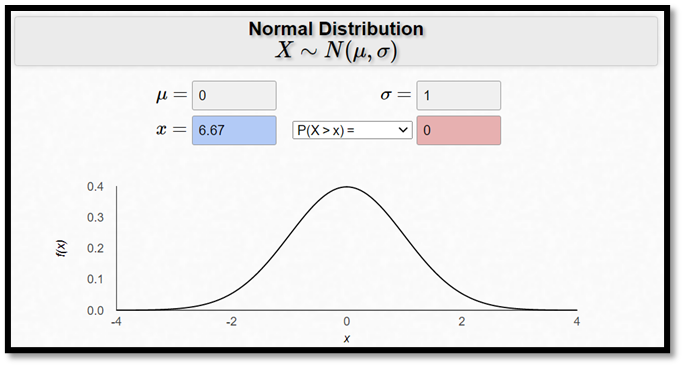
Om vi istället slumpmässigt samplade 100 personer så vore det praktiskt taget omöjligt att få ett stickprovsmedelvärde på 110+:
\[P\left( \overline{X} \geq 110 \right) \approx P(Z \geq 6,67) \approx 0\]
där
\[z = \frac{\overline{x} - \mu}{\sigma_{\overline{x}}} = \frac{110 - 100}{15/\sqrt{100}} \approx 6,67\]
Exempel. En vuxen människas vikt är normalfördelad med ett medelvärde på 80 och en standardavvikelse på 10. En hiss kan transportera upp till 400 kilo. Vilken begränsning ska man då sätta på antalet personer som får åka hissen samtidigt, om man vill se till att dessa tillsammans väger max 400 kilo med en sannolikhet på minst 99 procent?
Låt oss testa. Om vi sätter begränsningen till 5 personer så kan dessa i snitt väga som mest 80 kilo. Och sannolikheten för att dom i snitt väger mer än detta är ju 50 procent:
\[P\left( \overline{X} \leq 80 \right) \approx P(Z \leq 0) = 0,5\]
där
\[z = \frac{\overline{x} - \mu}{\sigma_{\overline{x}}} = \frac{80 - 80}{10/\sqrt{5}} = 0\]
5-personers begränsning är alltså för generöst. Hur är det med 4 personer? Dessa får då, i snitt, väga som mest 100 kilo. Sannolikheten för att detta ska inträffa är:
\[P\left( \overline{X} \leq 100 \right) \approx P(Z \leq 4) = 0,99997\]
där
\[z = \frac{\overline{x} - \mu}{\sigma_{\overline{x}}} = \frac{100 - 80}{10/\sqrt{4}} = 4\]
Fyra personer är alltså en lämplig begränsning. Sannolikheten för att dessa tillsammans ligger under 400-kiloskravet är ju över 99 procent. Detsamma skulle förstås gälla om vi satte begränsningen till tre, två, en eller noll personer. Men det vore å andra sidan onödigt strängt.
Ovan testade vi oss fram, men vi kunde också ha löst problemet på ett mer direkt sätt: Vi söker det antal personer (n) som ger en standardiserad medelvikt på 2,32635:
Vi vill alltså lösa ut n i ekvationen:
\[z = \frac{\overline{x} - \mu}{\sigma_{\overline{x}}} = \frac{\frac{400}{n} - 80}{10/\sqrt{n}} = 2,32635\]
Detta ger att n ≈ 4,39.
Det kan vara värt att notera att dessa beräkningar bara är korrekta om vi tänker oss att personerna som går in i hissen kan betraktas som ett slumpmässigt sampel från populationen. Om vi tvärtom tänker oss att viktväktarna eller bodybuilding-klubben har en lägenhet i huset så kanske maxvikten överskrids för ofta med denna begränsning. Eller om vi tänker oss att syskon ofta delar hiss och att dessa i viss mån tenderar likna varandra, så kanske också maxvikten överskrids för ofta.
Centrala gränsvärdessatsen
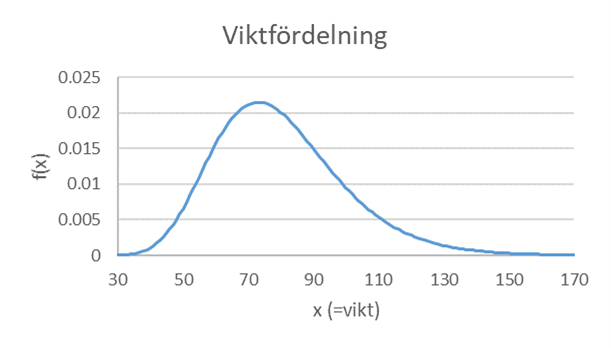
Exempel forts. Tidigare tänkte vi oss att en människas vikt är normalfördelad, men det vore här mer realistiskt att anta att vikten är lognormalfördelad. Figuren nedan illustrerar en sådan fördelning. Här är medelvärdet 80 och standardavvikelsen 20.
I en studie vill man uppskatta hur mycket finländare väger i genomsnitt. Anta att man slumpmässigt väljer ut 100 finländare från fördelningen ovan. Hur stor är sannolikheten för att få ett sampel där stickprovsmedelvärdet hamnar minst 3 kilo fel? Alltså ett medelvärde på 77 eller mindre, alternativt 83 eller mer?
\[P\left( \overline{X} \leq 77 \right) + P(\overline{X} \geq 83)\]
För att kunna besvara denna fråga så behöver vi kunskap om samplingfördelningen för stickprovsmedelvärdet. Vi känner redan till medelvärdet och standardavvikelsen i denna fördelning:
\[\mu_{\overline{x}} = \mu = 100\]
\[\sigma_{\overline{x}} = \frac{\sigma}{\sqrt{n}} = \frac{20}{\sqrt{100}} = 2\]
Men vilken fördelningsform följer då samplingfördelningen för stickprovsmedelvärdet i detta fall? Man skulle här kanske gissa att det är frågan om en lognormalfördelning – populationen är ju lognormalfördelad – men så är det inte. Stickprovsmedelvärdet följer nämligen fortsättningsvis en normalfördelning, åtminstone ungefärligt. Låter det kontraintuitivt? Låt oss testa! Jag drar slumpmässigt 100 personer från fördelningen ovan och räknar ut stickprovsmedelvärdet. Nedan visas ett utdrag av data:
69,6 97,9 102,1 51,9 47,2 59,8 71,0 51,8 80,2 88,4 85,9 … 80,1
Medelvärdet hamnade på 81,669. Det är alltså frågan om en överskattning med ca 1,7 kilo. Jag upprepar nu detta: jag drar ett nytt sampel – återigen 100 personer – och räknar ut ett nytt stickprovsmedelvärde. Denna gång blev medelvärdet 80,162. Och så upprepar jag det en tredje gång och får ett medelvärde på 81,848. Och jag slutar inte heller här. Totalt sett drar jag 100 000 sampel – alla bestående av 100 observationer vardera – och räknar ut 100 000 stickprovsmedelvärden. Tabellen nedan visar ett utdrag av resultatet.
| Sampel # | Stickprovsmedelvärde |
|---|---|
| 1 | 81,669 |
| 2 | 80,162 |
| 3 | 81,848 |
| 4 | 79,188 |
| 5 | 80,226 |
| ... | NA |
| 99 999 | 82,125 |
| 100 000 | 81,062 |
Figuren nedan beskriver fördelningen för dessa 100 000 stickprovsmedelvärden. Det här är med andra ord samplingfördelningen för stickprovsmedelvärdet. (Om vi ska vara helt korrekta så vore detta samplingfördelningen först när vi låter antalet sampel gå mot oändligheten.)
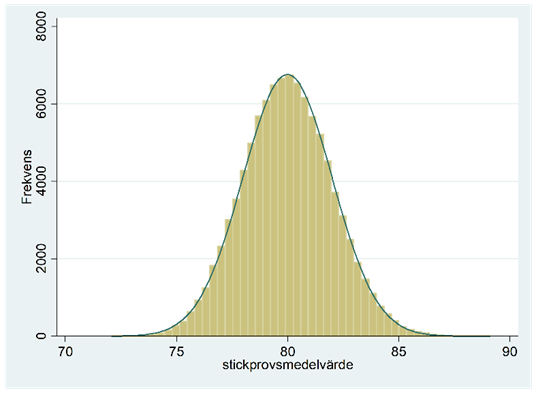
Det vi har fått är en normalfördelning trots att observationerna är dragna från en lognormalfördelning! Det här är resultatet av det som kallas för centrala gränsvärdessatsen. Den säger i korthet att samplingfördelningen för ett stickprovsmedelvärde är en normalfördelning, åtminstone ungefärligt. Det här gäller åtminstone om samplet är tillräckligt stort och slumpmässigt draget. Det här är en extremt användbar sats; den gör det möjligt för oss sätta sannolikheter på vad som kommer att hända när vi drar ett sampel från en population – oavsett hur den populationen ser ut!
Så hur stor är då sannolikheten för att få ett sampel där stickprovsmedelvärdet över- eller underskattar sanningen (µ = 100) med minst 3 kilo? I de 100 000 sampel jag drog har detta inträffat i 13 499 fall av 100 000 eller i 13,5 procent av fallen. Det här ligger nära den teoretiska sannolikheten på 13,4 procent:
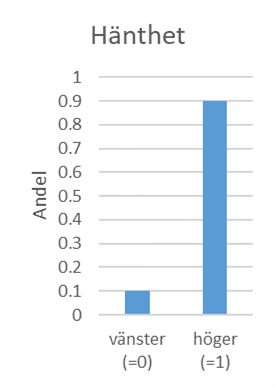
Exempel. Anta att 90 procent av befolkningen är högerhänta, vilket illustreras i populationsfördelningen nedan där högerhänta har värdet 1 och vänsterhänta värdet 0. Här gäller att populationsmedelvärdet ligger på 0,9; variansen och standardavvikelsen ligger på 0,09 respektive 0,3:
\[\mu = 0 \times 0,1 + 1 \times 0,9 = 0,9\]
\[\sigma^{2} = E\left( X^{2} \right) - \mu^{2} = 0,9 - {0,9}^{2} = 0,09\ \ \ \ \ \ \ = > \ \ \ \ \ \ \ \sigma = 0,3\]
\[ \text{där } E\!\left( X^{2} \right) = 0^{2} \times 0,1 + 1^{2} \times 0,9 = 0,9 \]
Vi samplar nu slumpmässigt 1000 personer från den här fördelningen. Hur stor är sannolikheten för att andelen högerhänta i samplet landar på minst 92 procent, dvs. en överskattning med minst två procentenheter?
Vi kan lösa det här problemet med hjälp av binomialfördelningen. Vi vill alltså beräkna sannolikheten för minst 920 gynnsamma utfall vid 1000 försök, där sannolikheten för ett gynnsamt utfall är 0,9. Den sökta sannolikheten är 0,0176. (Testa själv att du vet hur du får fram denna siffra!) Men vi kan också approximera denna sannolikhet med hjälp av normalfördelningen. “Andelen högerhänta i samplet” är ju ett stickprovsmedelvärde, och vi vet ju att stickprovsmedelvärdet följer en normalfördelning (åtminstone ungefärligt) även om populationsfördelningen inte gör det! I det här fallet är populationsfördelningen långt från en normalfördelning, men å andra sidan har vi ett stort sampel (1000 observationer) vilket torde vara mer än tillräckligt för en bra uppskattning.
Väntevärdet och standardavvikelsen i samplingfördelningen för stickprovmedelvärdet ges av:
\[\mu_{\overline{x}} = \mu = 0,9\]
\[\sigma_{\overline{x}} = \frac{\sigma}{\sqrt{n}} = \frac{0,3}{\sqrt{1000}} = 0,009487\ldots\]
Den sökta sannolikheten är:
\[P\left( \overline{X} \geq 0,92 \right) \approx P(Z \geq 2,108) \approx 0,0175\]
där
\[z = \frac{0,92 - 0,9}{0,009487\ldots} \approx 2,108\]
Den egentliga sannolikheten ligger alltså på 0,0176 men med hjälp av centrala gränsvärdessatsen kunde vi approximera denna sannolikhet till 0,0175.
Vi ska avsluta det här kapitlet med en notering gällande begreppet samplingfördelning. En samplingfördelning är en sannolikhetsfördelning, men inte för vilken variabel som helst, utan för en statistiska. T-fördelningen är alltså ett exempel på en samplingfördelning, för den beskriver sannolikheten för olika t-värden och t-värdet är en statistiska, dvs. ett mått som beräknas utifrån observationerna i ett sampel (samt kända konstanter). Samplingfördelningen för stickprovsmedelvärdet beskriver alltså hur pass sannolikt det är att få olika stickprovsmedelvärden då vi väljer ut ett visst antal individer från en population. Men vi kunde också tala om samplingfördelningen för maxvärdet eller, säg, medianen. Med hjälp av samplingfördelningen för maxvärdet kunde vi till exempel räkna ut sannolikheten för att den tyngsta personen väger över 100 kilo när fyra personer går in i en hiss samtidigt. I de allra flesta fall är dock medelvärdet av betydligt större intresse i statistiska tillämpningar. Därför har vi tittat specifikt på denna samplingfördelning här. Centrala gränsvärdessatsen visar att samplingfördelningen för stickprovsmedelvärdet är en normalfördelning (åtminstone ungefärligt för tillräckligt stora och slumpmässigt dragna sampel). I det här kapitlet har vi använt detta resultat för att säga vad vi kan dra för slutsatser om ett sampel draget från en viss population. I praktiken är vi dock oftast ännu mer intresserade av det omvända: Vad kan vi dra för slutsatser om en population på basen av ett sampel? Vi ska se på det i nästa kapitel.
Övningsuppgifter
Vad är en sannolikhet?
- I en stad finns två sjukhus, ett stort och ett litet. På det stora sjukhuset föds det i snitt 45 bebisar per dag, på det lilla 15. I långa loppet är 50 procent av bebisarna pojkar (gäller båda sjukhusen). Vi gör nu upp statistik över könsfördelningen bland bebisarna dag för dag i respektive sjukhus under loppet av ett år. Vilket av sjukhusen kommer sannolikt ha fler dagar där minst 80 procent av de nyfödda är pojkar? Är det:
Det stora sjukhuset
Det lilla sjukhuset
Sjukhusen förväntas ha lika många sådana dagar
Förklara ditt resonemang. (Exemplet hämtat från Tversky med kollegor.)
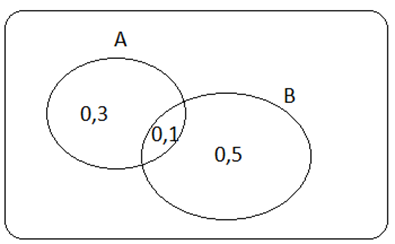
- Se venndiagrammet nedan. Sannolikheten för A är 0,3, sannolikheten för B är 0,5 och snittsannolikheten är 0,1. Hur stor är sannolikheten för att varken A eller B ska inträffa?
- Bland studerande är det 25 procent som äger en bil och 80 procent som äger en cykel.
Anta att 15 procent äger både bil och cykel. Hur stor procent av studerande äger då åtminstone ett av fordonen (bil eller cykel)?
Anta att 85 procent äger åtminstone ett av fordonen (bil eller cykel). Hur stor procent äger då både bil och cykel?
- En studerande måste välja ett av ämnena konstvetenskap, geologi eller psykologi som biämne.
Sannolikheten att hon väljer geologi är dubbelt större än sannolikheten att hon väljer konstvetenskap som i sin tur är lika stor som sannolikheten att hon väljer psykologi. Hur stor är sannolikheten för respektive biämne?
Anta nu att studenten ska välja (exakt) två biämnen. Hon väljer konstvetenskap med en sannolikhet på 5/8 och psykologi med en sannolikhet på 5/8; hon väljer kombinationen konstvetenskap och psykologi med en sannolikhet på 1/4. Hur stor är sannolikheten att hon väljer geologi?
Se uppgift b: Hur stor är sannolikheten att hon väljer konstvetenskap eller psykologi?
(Uppgiften hämtad ur Grinstead och Snells Introduction to Probability)
- Carl Sagan myntade begreppet “Extraordinary claims require extraordinary evidence.” Eller med andra ord: Om du hävdar något otroligt (“ett UFO har landat på min bakgård”) så krävs det mycket starka belägg för att det påståendet ska bli trovärdigt. Förklara på vilket sätt Bayes teorem säger exakt samma sak. (Ta hjälp av formeln i din förklaring.)
- Tabellen nedan bygger på data för ensamstående pensionärer. (Exempel: 11 procent av pensionärerna är manliga kattägare.) Vi väljer slumpmässigt ut en sådan pensionär.
| Har katt | Har inte katt | |
|---|---|---|
| Man | 0,11 | 0,34 |
| Kvinna | 0,25 | 0,30 |
Hur stor är sannolikheten att denna är en man?
Hur stor är sannolikheten att denna har en katt?
Hur stor är sannolikheten att denna är en man, givet att den är kattägare?
- Se påståendet nedan. Är det sant eller falskt? Förklara!
Du singlar en slant 1000 gånger på raken. Påståendet: Sannolikheten för att myntet landar krona upp varje gång är lika stor som sannolikheten för vilken annan given sekvens av krona och klave som helst.
- Risken för att dö efter en hjärtattack är 5 procent. En kväll anländer 10 personer till akutmottagningen efter en hjärtattack.
Hur stor är chansen att alla 10 överlever?
Hur stor är risken att minst en avlider?
- På en arbetsplats genomgår alla anställda ett oväntat test för droganvändning. Givet att en anställd använt drogen ifråga så kommer testet att visa positivt i 98 procent av fallen. Givet att en anställd inte använt drogen så kommer testet att visa negativt i 96 procent av fallen. Anta att 0,5 procent av befolkningen använder denna drog. Hur stor är sannolikheten att en anställd är droganvändare, givet att testet ger ett positivt resultat?
- Den här uppgiften presenterades först som en paradox av Martin Gardner. En familj har två barn.
Hur stor är sannolikheten att detta är två pojkar, givet att den förstfödda är pojke?
Hur stor är sannolikheten att detta är två pojkar, givet att åtminstone en av dem är pojke?
Sannolikhetsfördelningar
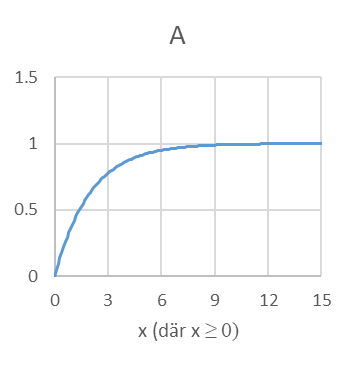
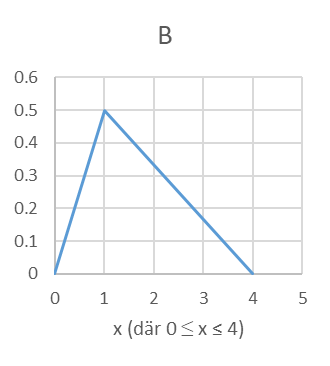
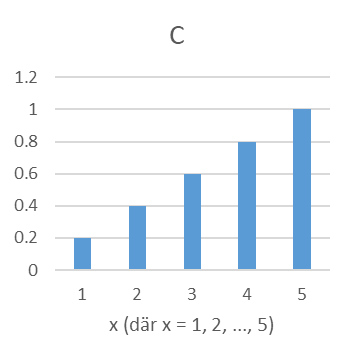
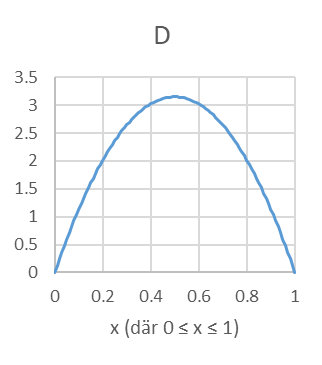
- En av nedanstående figurer är en sannolikhetsfördelning, två är kumulativa sannolikhetsfördelningar och en fjärde är varken eller. Ange för varje figur (A, B, C och D) vilken typ av fördelning det är frågan om.
- Ett gym håller register över hur mycket salarna används av kunderna. Låt X beteckna tiden (i timmar per vecka) som en kund använder gymmet. Nedan ges sannolikhetsfördelningen för X samt den kumulativa fördelningsfunktionen.
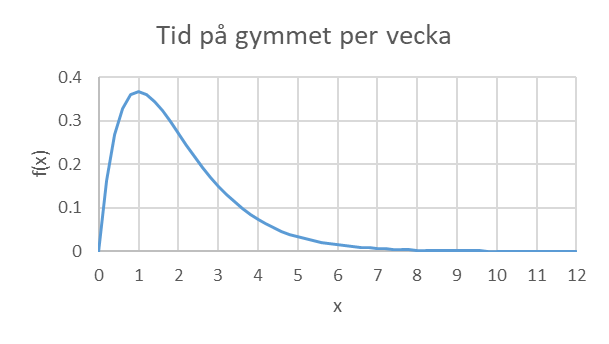
\[f(x) = xe^{- x}\ \ \ \ \ \ \ \ \ \ där\ x\ \geq 0\]
\[F(x) = 1 - e^{- x}(1 + x)\ \ \ \ \ \ \ \ \ där\ x\ \geq 0\]
Hur stor är procent av kunderna använder gymmet max en timme per vecka?
Hur stor procent av kunderna använder gymmet minst tre timmar per vecka?
Hur stor procent av kunderna använder gymmet 1-3 timmar per vecka?
Hur stor är sannolikheten att en kund använder gymmet 1-3 timmar per vecka, om vi vet att denna använder gymmet minst 1 timme per vecka?
- Tänk dig en aktie som kostar 20 euro i dag. Tills i morgon kan aktien antingen öka i värde med en euro, sjunka i värde med en euro, eller förbli oförändrad i värde. Sannolikheterna för dessa scenarion är 0,5, 0,3 och 0,2.
Hur mycket förväntas aktien öka i värde?
Vad är variansen och standardavvikelsen för förändringen i aktiens värde?
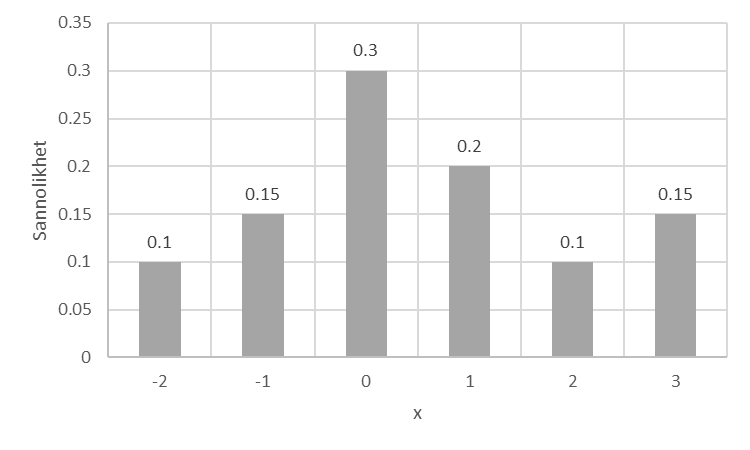
- Se sannolikhetsfördelningen nedan. Beräkna väntevärde och varians.
- På en tentamen finns en flervalsfråga med fyra alternativ varav ett korrekt. Rätt svar ger 1 poäng. Hur många poäng ska man dra ifrån för ett felaktigt svar, så att en student som gissar slumpmässigt förväntas få 0 poäng?
- På en ö bor 200 invånare varav alla vaccineras mot en livsfarlig sjukdom. Sannolikheten för att råka ut för en biverkning av vaccinet är 20 procent.
Hur många invånare förväntas få en biverkning?
[Kräver online-kalkylator] Hur stor är sannolikheten att minst 25 procent av öns invånare får en biverkning?
- På Amazon skickar kunder tillbaka varor som innehåller ett produktionsfel. Anta att en viss kattryggsäck har ett sådant produktionsfel i 10 procent av fallen (och ryggsäcken skickas då tillbaka av kunden, annars behåller denna ryggsäcken). En vecka säljer Amazon 1000 dylika ryggsäckar. En ryggsäck som levereras till kunden utan produktionsfel ger Amazon en vinst på 10 dollar. En ryggsäck med produktionsfel ger Amazon en kostnad på 60 dollar.
Hur stor vinst förväntas Amazon göra på den här försäljningen?
[Kräver online-kalkylator] Hur stor är sannolikheten att de gör en vinst på minst 3700 dollar på den här försäljningen?
- [Kräver online-kalkylator eller tabell] I vissa länder har man noterat följande paradox: Männen har i snitt sämre avgångsbetyg från gymnasiet, men ändå större chans än kvinnorna att bli antagna till de bästa utbildningarna. Hur är det möjligt? Figuren nedan ger svaret. I blått visas fördelningen för männens meritpoäng från gymnasiet och i rött visas fördelningen för kvinnornas. Båda är normalfördelade. Kvinnorna snittar 100 poäng och männen 95; kvinnornas standardavvikelse är 10 poäng och männens 16.
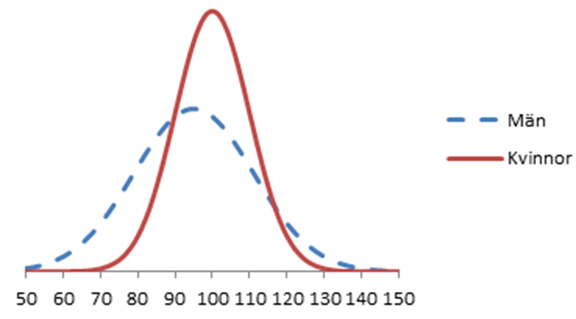
En läkarutbildning antar enbart personer som fått minst 120 meritpoäng i avgångsbetyg. Hur stor procent av kvinnorna skulle bli antagna om de sökte? Hur stor procent av männen?
Samplingfördelningar
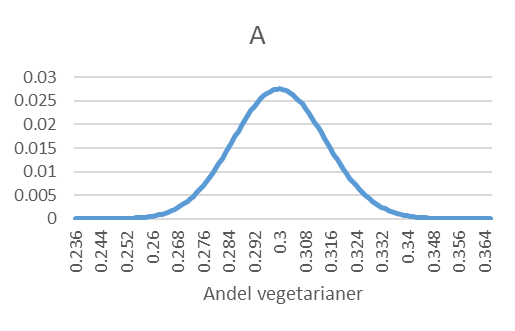
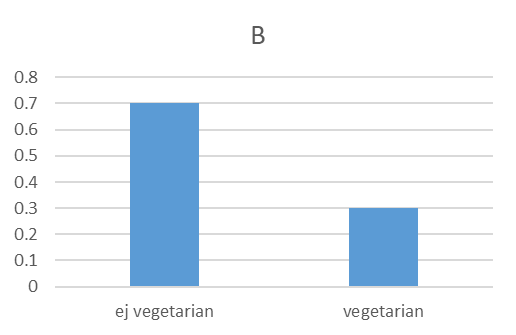
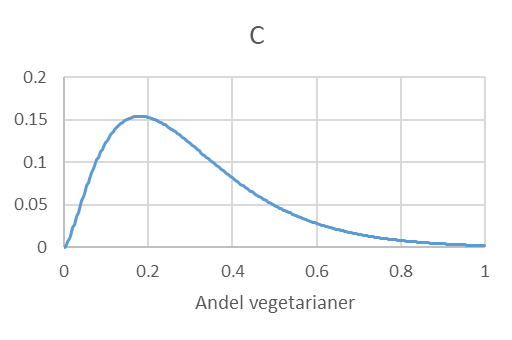
- Vi väljer slumpmässigt ut 1000 personer från en population där 30 procent är vegetarianer. Låt \(\widehat{p}\) beteckna andelen vegetarianer i samplet. Vilken av följande figurer (A, B eller C) representerar samplingfördelningen för \(\widehat{p}\)? Förklara kortfattat.
- I Zimbabwe lever invånarna i snitt på 3 dollar per dag (µ = 3) med en standardavvikelse på 3 dollar per dag (σ = 3).
[Kräver online-kalkylator eller tabell] Du samplar slumpmässigt 900 invånare. Hur stor är sannolikheten för att du får ett sampel där medelvärdet blir 2,9 dollar eller mindre?
Förklara på vilket sätt du dragit nytta av centrala gränsvärdessatsen för att lösa uppgift a.
- [Kräver online-kalkylator eller tabell] Anta att vuxna finländare sover 8 timmar per natt i genomsnitt (µ = 8) med en standardavvikelse på 1 timme (σ = 1). Du drar nu ett slumpmässigt sampel individer från den här populationen. Hur stor är sannolikheten för att få ett sampel där stickprovsmedelvärdet prickar fel med minst 0,1 timmar givet att …
du samplar 100 personer?
du samplar 400 personer?
Hur många personer bör du sampla, om du vill se till att stickprovsmedelvärdet hamnar någonstans i intervallet 7,9-8,1 timmar med en sannolikhet på 99 procent?
Om du tycker att detta är paradoxalt så är du inte ensam. Paradoxen ligger i att varje enskild kund ändå har en exakt betjäningstid; när nästa person blir betjänad så kommer ju något att hända, dvs. personen kommer att få en betjäningstid. Men om sannolikheten för en viss betjäningstid är noll … hur går det ihop? Paradoxens lösning ligger i att en sannolikhet på noll är inte detsamma som att ett visst utfall är omöjligt. Det här skulle stämma i en diskret värld, men inte i en kontinuerlig. (På motsvarande sätt: Om vi sätter ihop oändligt många punkter där var och en har en längd på noll, så kan dessa sammantaget ändå få en positiv längd.)↩︎