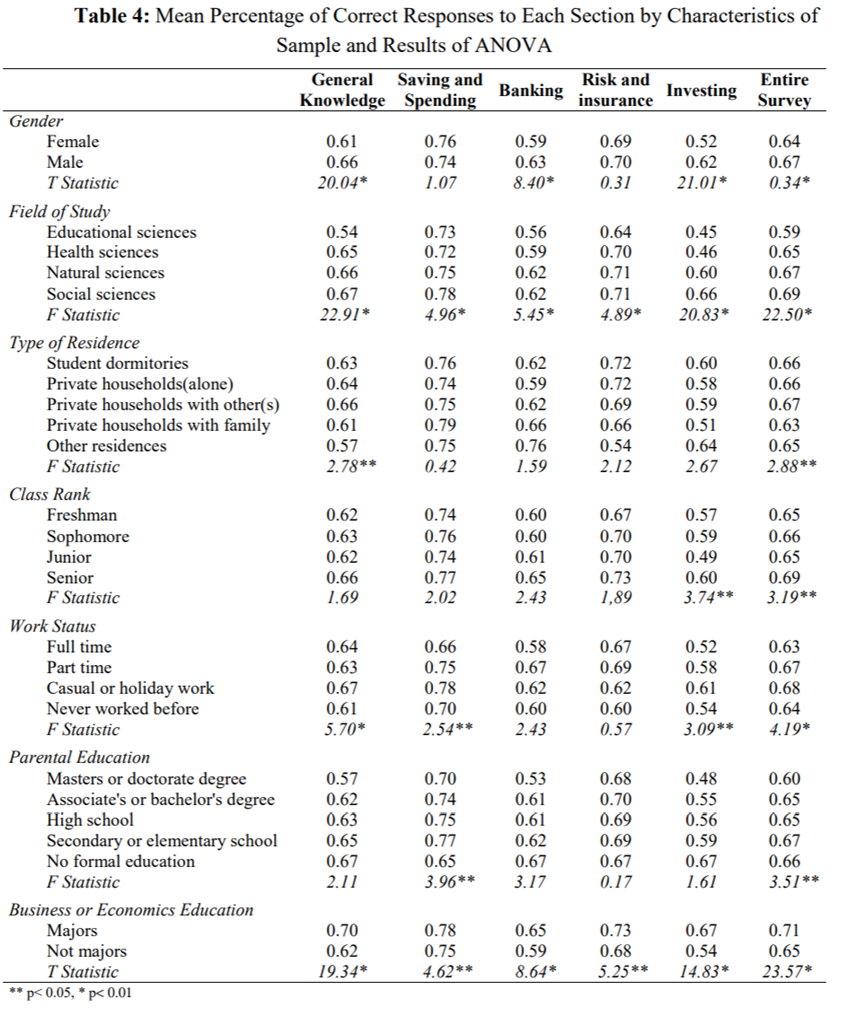
| id | egenföretagare | ålder | ln(timlön) |
|---|---|---|---|
| 1 | 0 | 32 | 1,955861 |
| 2 | 1 | 31 | 0,357674 |
| 3 | 1 | 44 | 3,021887 |
| 4 | 0 | 64 | 1,011601 |
| 5 | 0 | 41 | 2,957511 |
| … | … | … | … |
| 293 | 0 | 35 | 0,364643 |
11 Test gällande en grupp koefficienter - ANOVA
När vi hittills diskuterat hypotesprövning så har vi testat om en viss effekt är signifikant och har då tagit hjälp av t-tester. Men alla hypoteser gäller inte enskilda effekter. I det här kapitlet och följande ska vi se exempel på andra sorters hypoteser som kräver andra test-statistikor. Vi ska då börja med F-statistikan. Vi ser bäst när vi kan ha användning av denna genom några exempel.
25. F-testet
11.1 Har modellen signifikant förklaringsstyrka?
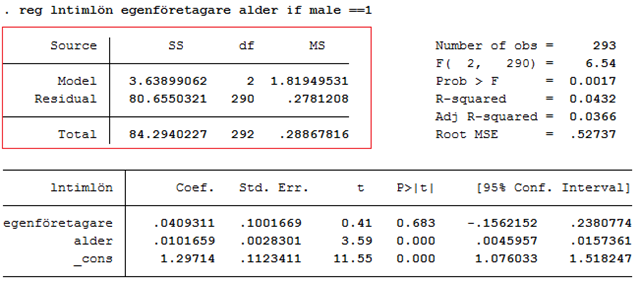
Exempel. Tjänar man mer som egenföretagare? Nedan visas ett utdrag ur ett datamaterial som innehåller information om 293 amerikanska manliga arbetare. Egenföretagare är en dummy som antar värdet 1 för egenföretagare och värdet 0 för anställda; alder mäter personens ålder och ln(timlön) är timlönen mätt på en loggad skala.
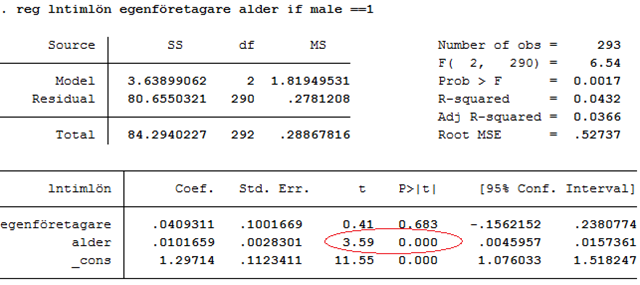
Regressionen nedan visar att egenföretagarna tjänar cirka 4 procent mer än anställda, kontrollerat för ålder. Men skillnaden är inte signifikant, t = 0,041/0,100 = 0,41 (standardfel ges inom parentes). Däremot har åldern en signifikant effekt på lönen; för varje ytterligare år så ökar lönen med cirka 1 procent, t = 0,010/0,003 \(>\) 3.
\[ \widehat{\ln(\text{timlön})} = 1,30 + \underset{\textstyle (0,100)}{0,041} \times \text{egenföretagare} + \underset{\textstyle (0,003)}{0,010} \times \text{ålder} \]
Nedan visas resultatet då vi kört regressionen med hjälp av statistikprogrammet STATA:
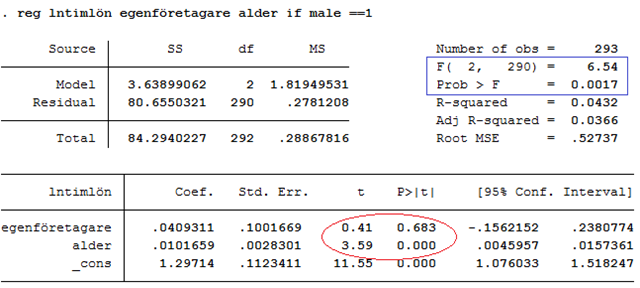
I rött ges resultatet från t-testerna. Men dessa är inte de enda tester som finns med i regressionsutskriften. Regressionsutskriften innehåller också ett annat test som kallas för F-testet. Inrutat i blått finns det så kallade F-värdet (6,54) med tillhörande p-värde (0,0017). Så vad använder vi detta test till? Jo, här kan vi se om regressionsmodellen som helhet har signifikant förklaringsstyrka. Eftersom p-värdet (0,0017) är mindre än 0,05 så är svaret ja. Vi ska nu se närmare på vad det här betyder. Och vi ska börja med att repetera förklaringsgraden.
Förklaringsgraden
Exempel forts. I regressionen ovan så är förklaringsgraden 0,0432. (Du hittar förklaringsgraden under F-testet: R-squared = 0,0432.) Det betyder att 4,32 procent av variationen i loggade löner kan förklaras av x-variablerna (egenföretagare, alder). Förklaringsgraden är alltså en andel och kan därför anta värden mellan 0 och 1.
Det kan vara bra att fundera på vad de två extremfallen betyder. Vad skulle det betyda om förklaringsgraden vore 1? Jo, att 100 procent av variationen i utfallsvariabeln (y) kan förklaras av x-variablerna; residualen är då noll för varje observation i data. Tabellen nedan visar data, tillsammans med prediktionerna och residualerna.
| id | egenföretagare | ålder | ln(timlön) | Prediktion | Residual |
|---|---|---|---|---|---|
| 1 | 0 | 32 | 1,955861 | 1,622449 | 0,333412 |
| 2 | 1 | 31 | 0,357674 | 1,653214 | −1,295540 |
| 3 | 1 | 44 | 3,021887 | 1,785371 | 1,236516 |
| 4 | 0 | 64 | 1,011601 | 1,947757 | −0,936157 |
| 5 | 0 | 41 | 2,957511 | 1,713942 | 1,243569 |
| … | … | … | … | … | … |
| 293 | 0 | 35 | 0,364643 | 1,652947 | −1,288304 |
Om alla residualer vore noll så skulle regressionen göra perfekta prediktioner för varje individ i data. Förklaringsgraden skulle vara 1.
Vad skulle det betyda om förklaringsgraden vore 0? Jo, det betyder att 0 procent av variationen i y förklaras av x-variablerna. Det här skulle innebära att vi hade en regression där alla regressionskoefficienter vore 0:
\[\widehat{ln(timlön)} = 1,69 + \mathbf{0} \times egenföretagare + \mathbf{0} \times alder\]
Om vi ändå använde den här regressionen för att göra prediktioner så skulle alla personer i data ha en predikterad loggad lön på 1,69. 1,69 är den genomsnittliga loggade lönen i data. Det här skulle betyda att x-variablerna inte bidrar med någon information alls; om vi ska gissa hur mycket en person tjänar så gör vi bäst i att bara använda medelvärdet.
F-värdet
Exempel forts. I regressionen ovan så är förklaringsgraden 0,0432. Men detta är förklaringsgraden i samplet: Är det möjligt att populationens förklaringsgrad egentligen är noll? Det skulle betyda att den sanna effekten av att vara egenföretagare är noll (βegen = 0) och att den sanna effekten av ålder är noll (βalder = 0). Vi kallar denna möjlighet för nollhypotesen.
Den andra möjligheten är att åtminstone en av effekterna (βegen, βalder) eller båda är olika noll. Eller med andra ord: Den sanna förklaringsgraden är större än noll. Vi kallar denna möjlighet för mothypotesen.
H0: βegen = 0, βalder = 0 \(\leftrightarrow\) populationens förklaringsgrad är 0
H1: Åtminstone en av effekterna (βegen, βalder) är olika 0 \(\leftrightarrow\) populationens förklaringsgrad är större än 0
Kan vi förkasta nollhypotesen om att populationens förklaringsgrad är noll? För att svara på den frågan så skulle vi vilja veta hur vanligt är det att få en förklaringsgrad på 0,0432 bara av slumpen. Är detta något som händer ofta då den sanna förklaringsgraden är noll, eller är detta något som händer sällan? Det går att räkna ut den sannolikheten: I det här fallet så är sannolikheten för att – bara av slumpen – få ett sampel där förklaringsgraden blir 0,0432 eller större 0,17 procent:
P(R2 \(\geq 0,0432) = 0,0017\)
Den uppmätta förklaringsgraden i samplet hör alltså till de 0,17 procent extremaste som man kan få bara av slumpen. Även om förklaringsgraden (0,0432) inte är särskilt stor, så är det alltså mycket osannolikt att få en så här “stor” förklaringsgrad bara av slumpen. Vi säger då att regressionsmodellen har signifikant förklaringsstyrka: p-värdet är 0,0017 som är mindre än 0,05. Eftersom p-värdet är mindre än 0,01 så har regressionsmodellen också signifikant förklaringsstyrka på 1-procentsnivån.
Notera här att p-värdet (0,0017) är samma p-värde som ges i regressionsutskriften, inrutat i blått:
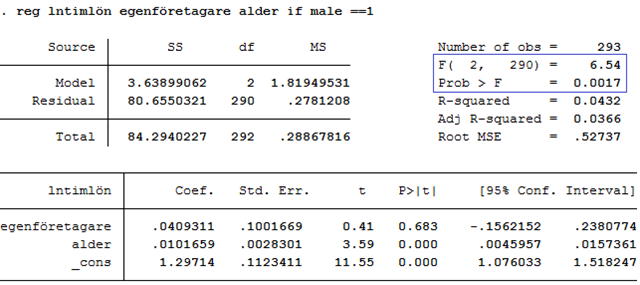
F-testet används alltså för att ta reda på om regressionsmodellen har signifikant förklaringsstyrka. Men varifrån kommer då F-värdet på 6,54?
F-värdet kan beräknas som en transformation av förklaringsgraden (R2):
\[ F = \frac{R^{2}/k}{(1 - R^{2})/(n - k - 1)} \]
där k är antalet oberoende variabler. Detta ger oss ett F-värde på 6,54:
\[ F = \frac{R^{2}/k}{(1 - R^{2})/(n - k - 1)} = \frac{0,0432/2}{(1 - 0,0432)/(293 - 2 - 1)} \approx 6,54 \]
Ju större förklaringsgrad, desto större F-värde. Om förklaringsgraden istället hade varit 0,5 så hade vi fått ett F-värde på 145:
\[ F = \frac{R^{2}/p}{(1 - R^{2})/(n - k - 1)} = \frac{0,5/2}{(1 - 0,5)/(293 - 2 - 1)} = 145 \]
När vi vill ta reda på sannolikheten för att – bara av slumpen – få ett sampel där förklaringsgraden blir minst 0,0432 så är det samma sak som att ställa sig frågan: Hur stor är sannolikheten för att – bara av slumpen – få ett F-värde på minst 6,54? Eller med andra ord:
\[P(R^{2} \geq 0,0432) = P(F \geq 6,54)\]
Vi såg redan att den sannolikheten är 0,0017. Figuren nedan illustrerar detta:
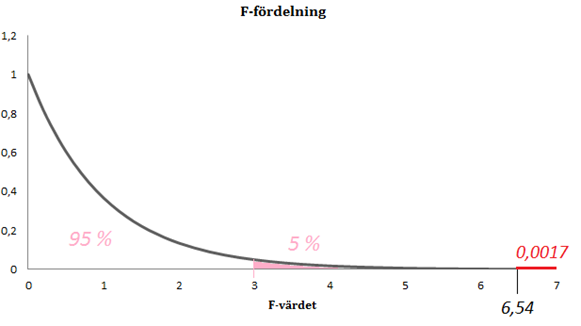
Det här är ett exempel på en F-fördelning. Om nollhypotesen är sann (den sanna förklaringsgraden är noll) så får vi ett sampel där F-värdet hamnar någonstans mellan 0 och 3 i 95 procent av fallen. (Ett F-värde någonstans mellan 0 och 3 motsvarar här en förklaringsgrad någonstans mellan 0 och 0,02.) Om vårt F-värde faller inom detta intervall så är resultatet insignifikant; den uppmätta förklaringsgraden i samplet skulle då kunna skyllas på slumpen. I 5 procent av fallen får vi dock ett F-värde som är större än 3. Om vi får ett sampel där F-värdet blir 3,0 så betyder det att samplet hör till de 5 procent mest extrema som man kan få bara av slumpen och p-värdet är då 0,05; vi har då ett bra stöd för att påstå att den sanna förklaringsgraden är större än 0. Men vi fick ett F-värde på 6,54 vilket ger ett p-värde på 0,0017. Regressionsmodellen har med andra ord signifikant förklaringsstyrka också på 1-procentsnivån: p-värdet = 0,0017 < 0,01.
Hur F-fördelningen ser ut varierar dock från fall till fall; sannolikheten för att – bara av slumpen – få ett sampel där F-värdet blir större än 6,54 beror också på antalet observationer (n) och antalet oberoende variabler (k). Det här betyder att F-fördelningens utseende varierar beroende på n och k. Man säger att F-fördelningen har två parametrar som bestämmer exakt hur den ser ut. Vi kan jämföra detta med normalfördelningen som också har två parametrar (µ och σ) som bestämmer hur normalfördelningen ser ut. F-fördelningens parametrar kallas för frihetsgradsantalet i täljaren och frihetsgradsantalet i nämnaren. Frihetsgradsantalet i täljaren är antalet oberoende variabler (\(\color{red}{k}\)); frihetsgradsantalet i nämnaren är antalet observationer (\(\color{blue}{n}\)) minus antalet oberoende variabler (\(\color{blue}{k}\)) minus ett:
\[ F = \frac{R^{2}/\color{red}k}{(1 - R^{2})/({\color{blue}{n - k - 1}})} \]
I vårt exempel har vi alltså 2 frihetsgrader i täljaren och 290 i nämnaren. Med hjälp av en kalkylator kan vi då få fram p-värdet:
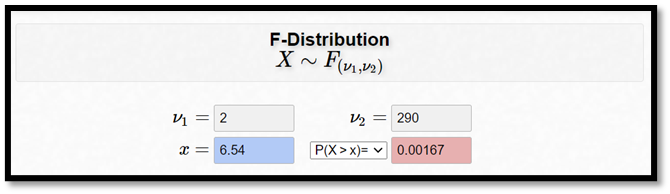
Det kan vara värt att notera här att F-testet är svårare att läsa av än t-testet. Om vi får ett t-värde som är större än 2 (absolut sett) så vet vi att resultatet är signifikant (såtillvida att samplet inte är mycket litet). Det här gäller alltså inte för F-testet; ett F-värde på 2 kan vara signifikant en gång men långt ifrån signifikant en annan gång. Därför skulle du aldrig se en statistisk rapport där man bara rapporterar F-värdet; man måste ge läsaren mer information, såsom antalet frihetsgrader eller p-värdet (eller båda).
T-test kontra F-test
Exempel forts. Vi beskrev noll- och mothypotesen:
H0: βegen = 0 och βalder = 0
H1: Åtminstone en av effekterna är olika noll
Ett signifikant resultat betyder att vi kan “förkasta nollhypotesen”. Men behöver vi verkligen ett F-test för att avgöra detta? Vi vet ju redan att åldern har en signifikant effekt på lönen:
Om åldern har en signifikant effekt på lönen så måste väl också F-testet per konstruktion visa att regressionsmodellen har signifikant förklaringsstyrka? Svaret är nej. Anta att nollhypotesen är sann; ingen x-variabel har någon effekt på utfallsvariabeln. Ju fler x-variabler vi inkluderar i regressionen, desto högre är sannolikheten för att åtminstone en effekt ändå blir signifikant. Nedan visas ett exempel på detta. Här har vi en regression med 20 oberoende variabler (x1, x2, …, x20). Ingen av dessa har egentligen någon effekt på utfallsvariabeln; de effekter vi ser i data beror enbart på slumpen. I de flesta fall har vi därför fått estimat som ligger nära 0 och som är icke-signifikanta. Men det finns ett misstag; t-testet visar att effekten av x4 är signifikant.
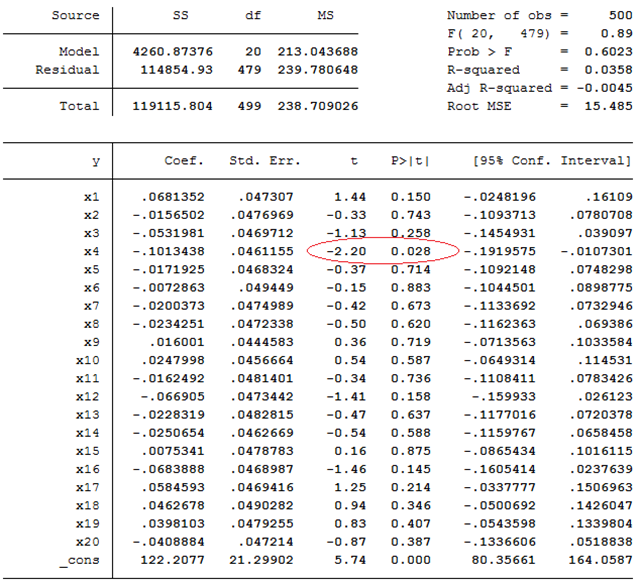
Ju fler t-tester, desto större är chansen för att åtminstone ett sådant här misstag begås. (På samma sätt som chansen för att få en sexa ökar ju fler gånger vi kastar en tärning.) Om, de facto, ingen av x-variablerna har någon effekt på utfallsvariabeln så kan vi ändå förvänta oss att 5 procent av effekterna blir signifikanta: Vi säger ju att en effekt är signifikant om den hör till de 5 procent extremaste som man kan få bara av slumpen – i 5 procent av fallen är slumpen framme och ger oss ett signifikant resultat av misstag.
I fallet ovan så är populationens sanna förklaringsgrad 0; ingen av de 20 x-variablerna har någon egentlig effekt på utfallsvariabeln. F-testet visar också att regressionsmodellen inte har signifikant förklaringsstyrka (F = 0,89, p-värdet = 0,6023).
På motsvarande sätt kan det också finnas situationer där F-testet blir signifikant trots att ingen av de enskilda t-testerna ger signifikanta resultat. I vissa regressioner är det tydligt att någon (eller flera) x-variabler har en effekt på utfallsvariabeln, men det är svårt att peka ut vilken eller vilka. Detta inträffar då x-variablerna är starkt korrelerade. Vi kan förstå detta genom följande analogi: Säg att du gått ner tio kilo efter att du börjat träna och ändrat diet. Det kan då vara svårt att avgöra om träningen eller dieten var orsaken (eller om bägge bidrog). Träning och diet är så att säga starkt korrelerade; du började med bägge samtidigt. Men även om det är svårt att påstå att “träningen har effekt” eller att “dieten har effekt” så är det lätt att påstå att “träningen eller dieten (eller båda) har effekt”, vilket skulle motsvara ett signifikant resultat på F-testet trots att ingen av de enskilda t-testerna är signifikanta.
En oberoende variabel: F = t^2
F-test och t-test används generellt sett för att besvara olika frågeställningar. Med ett undantag: Om vi bara har en oberoende variabel så är t-testet och F-testet exakt samma sak.
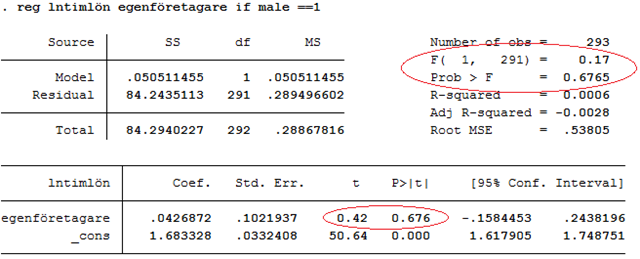
Exempel forts. Nedan visas resultat från en regression med loggad timlön som utfallsvariabel och dummyn egenföretagare som oberoende variabel. Här har vi alltså inte kontrollerat för ålder. Egenföretagarna tjänar i snitt drygt 4 procent mer än anställda, men skillnaden är inte signifikant (t = 0,42, p-värdet = \(\color{red}{0,676}\)). Regressionsmodellen har inte heller signifikant förklaringsstyrka (F = 0,17, p-värdet = \(\color{red}{0,6765}\)). Notera här att p-värdena är lika stora. Detta beror på att bägge testar exakt samma sak. När vi bara har en oberoende variabel så kommer vi från t-värdet till F-värdet genom att kvadrera t-värdet: 0,422 \(\approx\) 0,17.
ANOVA: Variansanalys
Se regressionstabellen nedan. Inrutat i rött visas en tabell som kallas för ANOVA. ANOVA är kort för ANalysis Of VAriances (variansanalys). Den här tabellen är ett sätt att beskriva de komponenter som ingår i F-värdet (eller i förklaringsgraden). Vi ska inte säga mer om just den saken i detta skede, men det kan vara bra att känna till själva begreppet (ANOVA) eftersom det är i flitig användning. Om man i en rapport gjort en variansanalys (ANOVA) så betyder det alltså att författarna använt ett F-test i något syfte. I nästa avsnitt ska vi se på ett tillfälle där F-testet används extra ofta.
11.2 Regressioner med faktorvariabler
Om du läser en statistisk rapport där man gjort en multipel regression så är chansen stor att de inte rapporterar resultatet från F-testet. Ofta ligger intresset i att estimera effekten av en x-variabel på utfallsvariabeln, kontrollerat för några andra variabler. F-testet i sig är inte då inte lika intressant.
Men det finns också fall där F-testet är av huvudsakligt intresse. Detta gäller inte minst då vi vill jämföra medelvärden mellan tre eller flera grupper, dvs. då vi kör regressioner med faktorvariabler.
Exempel. Vi ska lansera en ny läskedryck och ska nu besluta oss för vilken färg vi vill använda på förpackningen. Vi utför följande experiment. Tio kvartersbutiker ingår i studien; fem av dessa lottas ut och får röda läskburkar medan de andra fem får blåa. Efter en vecka mäter vi försäljningen i varje butik (mätt som antalet backar). Tabellen nedan visar data.
| Butik | Färg | Röd | Försäljning |
|---|---|---|---|
| 1 | Blå | 0 | 5 |
| 2 | Blå | 0 | 7 |
| 3 | Blå | 0 | 5 |
| 4 | Blå | 0 | 6 |
| 5 | Blå | 0 | 2 |
| 6 | Röd | 1 | 9 |
| 7 | Röd | 1 | 7 |
| 8 | Röd | 1 | 6 |
| 9 | Röd | 1 | 7 |
| 10 | Röd | 1 | 6 |
I genomsnitt såldes 5 backar av de blåa burkarna och 7 backar av de röda. Det är en genomsnittlig skillnad på 2 backar. Eller uttryckt som en regression: \(\widehat{försäljning} = 5 + 2 \times röd\).
Är skillnaden signifikant? Nästan. Standardfelet för skillnaden är 1 vilket ger ett t-värde på 2 (t = 2/1 =2). Detta motsvarar ett p-värde på 0,081. (I det här exemplet räcker ett t-värde på 2 inte riktigt till för att skillnaden ska bli signifikant på 5-procentsnivån. Detta beror på att samplet är så pass litet, bara tio observationer.)
Men anta nu att vi istället hade gjort följande experiment: Vi använder nu 15 butiker varav fem lottas ut för att få röda burkar; fem får blåa burkar och fem får svarta. Ett utdrag av data visas nedan:
| Butik | Färg | Röd | Blå | Försäljning |
|---|---|---|---|---|
| 1 | Blå | 0 | 1 | 5 |
| 2 | Blå | 0 | 1 | 7 |
| 3 | Blå | 0 | 1 | 5 |
| 4 | Blå | 0 | 1 | 6 |
| 5 | Blå | 0 | 1 | 2 |
| 6 | Röd | 1 | 0 | 9 |
| 7 | Röd | 1 | 0 | 7 |
| 8 | Röd | 1 | 0 | 6 |
| 9 | Röd | 1 | 0 | 7 |
| 10 | Röd | 1 | 0 | 6 |
| 11 | Svart | 0 | 0 | 4 |
| 12 | Svart | 0 | 0 | 4 |
| 13 | Svart | 0 | 0 | 4 |
| 14 | Svart | 0 | 0 | 1 |
| 15 | Svart | 0 | 0 | 2 |
I genomsnitt såldes 5 backar av de blåa burkarna; 7 backar av de röda och 3 backar av de svarta. Uttryckt som en regression så kan vi beskriva dessa skillnader som:
\[\widehat{försäljning} = 3 + {\color{red}{4 \times röd}} + {\color{blue}{2 \times blå}}\]
där referensgruppen är svarta burkar. Färg kallas här för en faktor; när vi inkluderar information om burkarnas färger genom en rad dummy-variabler så har vi gjort en regression med en faktorvariabel.
Har regressionen signifikant förklaringsstyrka? Svaret är ja: F-värdet är 8,57 och p-värdet är 0,0049:
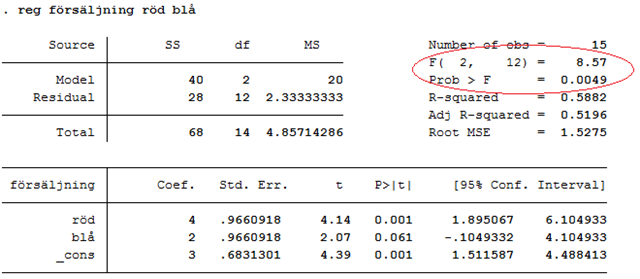
Regressionsmodellen har med andra ord också signifikant förklaringsstyrka på 1-procentsnivån (0,0049 < 0,01). Eller med andra ord: Vi kan förkasta nollhypotesen om att den sanna förklaringsgraden är noll. Men i det här exemplet så kan vi också formulera nollhypotesen på ett annat mer intuitivt sätt:
H0: \(\mu_{svarta} = \mu_{röda} = \mu_{blå}\)
Om den sanna förklaringsgraden är noll så betyder det att försäljningen inte varierar beroende på burkens färg eller med andra ord: Genomsnittlig försäljning är lika stor oavsett färg: \(\mu_{vita} = \mu_{röda} = \mu_{blå}\). Detta är i sin tur samma sak som att säga att det inte finns några verkliga genomsnittliga skillnader mellan röda och svarta burkar, eller mellan blåa och svarta burkar: βröda = 0, βblå = 0.
H1: Åtminstone en av grupperna (vita, röda, blåa) skiljer sig från de övriga.
I det här fallet kunde vi konstatera att det finns signifikanta skillnader i genomsnittlig försäljning beroende på burkens färg. F-testet säger dock inte vilka färger som skiljer sig signifikant från andra; eller om det finns signifikanta skillnader mellan alla tre färger.
Övningsuppgifter
Har modellen signifikant förklaringsstyrka?
- Nedan visas en löneregression med loggad lön som utfallsvariabel; facket är en dummy som antar värdet 1 för fackmedlemmar och värdet 0 för övriga; utbildning mäter utbildning i antal år. Standardfel ges inom parentes. Samplet består av 245 kvinnliga amerikanska arbetstagare. Har regressionsmodellen signifikant förklaringsstyrka? I så fall, på vilken nivå? De kritiska värdena på 10-, 5- och 1-procentsnivån är 2,32, 3,03 och 4,69.
\[ \widehat{\ln(\text{lön})} = 0,69 + \underset{\textstyle (0,094)}{0,217} \times \text{facket} + \underset{\textstyle (0,011)}{0,094} \times \text{utbildning} \qquad R^{2} = 0,24 \]
- I en studie vill man ta reda på om det finns skillnader i intelligens beroende på stjärntecken. Man låter hundratals personer skriva ett intelligenstest och frågar också om deras stjärntecken. Sedan gör man totalt 66 stycken t-tester; ett där man ser om det finns en signifikant skillnad i intelligens mellan väduren och oxen; ett annat där man ser om det finns en signifikant skillnad mellan oxen och tvillingarna, osv. (När man gjort alla parvisa jämförelser så adderar detta till 66 tester). Man får totalt tre stycken signifikanta skillnader och drar slutsatsen att det finns skillnader i intelligens mellan dessa stjärntecken. Förklara vad som är fel med denna slutsats.
Regressioner med faktorvariabler
- [Kräver online-kalkylator] I en studie ger man 160 personer varsin stegräknare. Man delar sedan in individerna i fyra grupper omfattande 40 personer vardera. Målet är att testa olika “incitamentssystem” för att motivera personerna att röra på sig mer. Exempel: I en grupp får den som gått mest under loppet av en månad en summa pengar. I en annan grupp får alla som gått minst 10 000 steg per dag ett diplom, osv. Figuren nedan visar hur många steg personerna tog per dag beroende på incitamentssystem. Förklaringsgraden är 0,064.
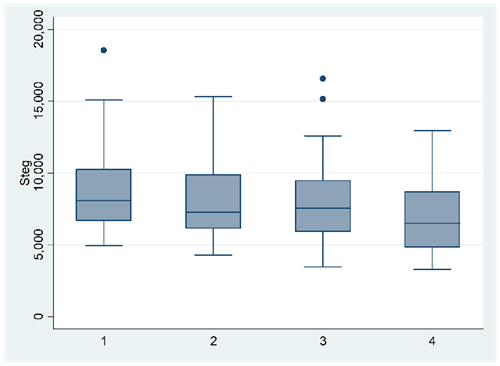
Testa:
H0: µ1 = µ2 = µ3 = µ4
H1: Åtminstone en av grupperna skiljer sig från de övriga
Ange också om resultatet är signifikant på 10-, 5- eller 1-procentsnivån.
- Tabellen nedan är hämtad ur artikeln A Survey on Financial Literacy Among University Students. Här har man låtit ett sampel studerande ta ett test som mäter hur bra koll de har på finansfrågor. Se kolumnen General Knowledge. Författaren har här gjort flera F-tester. Beskriv i ord vad författaren egentligen testat här och sammanfatta resultatet. Notera också att författaren ibland använt t-testet och ibland F-testet. Varför tror du det är fallet?