| ID | Kön | Ålder | Hälsa | Hästar |
|---|---|---|---|---|
| 1 | Man | 32 | God | 5 |
| 2 | Kvinna | 48 | Utmärkt | 4 |
| 3 | Kvinna | 20 | God | 5 |
| 4 | Kvinna | 66 | Ganska svag | 3 |
| 5 | Man | 45 | Mycket svag | 2 |
| 6 | Man | 35 | Utmärkt | 2 |
2 Beskrivande statistik för en variabel
Här visas ett utdrag av data som beskriver livslängden i världens länder:
61, 77, 71, 51, 76, 76, 74, 82, 81, 71, 75, 76, 70, 75, 70, 80, 74, 59, 68, 67, 76, 47, 74, 78, 73, 56, 54, 72, 55, 81, 75, 50, 51, 80, 75, 74, 61, 50, 58, 80, 50, 77, 79, 80, 78, 79, 61, 73, 76, 71, 72, 53, 62, 74, 63, 70, 80, 82, 63, 59, 74, 81, 61, 81, 71, 73, 72, 56, 54, 66, 63, 74, 83, 74, 83, 74, 82, 66, 71, …
Den här uppräkningen av siffror är förstås svår att överblicka. För att kunna använda informationen så måste vi börja med att sammanställa den på ett överskådligt sätt. I det här kapitlet lär vi oss hur.
En möjlighet är att rita upp en figur som illustrerar materialet. Hit hör till exempel histogrammet. En annan möjlighet är att sammanfatta data genom beskrivande mått. De två populäraste är medelvärdet och standardavvikelsen. Men innan vi går in på olika figurer och mått så ska vi se på hur man ställer upp ett datamaterial i en datamatris.
1. Beskrivande statistik, del 1
2. Beskrivande statistik, del 2
3. Beskrivande statistik, del 3
2.1 Datamatrisen
För att samla in data så kan man exempelvis använda sig av enkäter:

Anta för enkelhetens skull att sex personer besvarar den här enkäten. Vi kallar det här datamaterialet för ett sampel. För att kunna jobba med samplet börjar vi med att sammanställa det i en datamatris:
I det här samplet är observationsenheten en person, dvs. vi har samlat in data gällande personer. I andra studier kanske man istället samlar in data gällande hushåll, kommuner, företag eller länder. I det sista fallet så är observationsenheten ett land.
Varje rad i datamatrisen är en observation. Här har vi sex rader, dvs. sex observationer. “Antalet observationer” säger med andra ord hur många personer som besvarat enkäten.
Varje kolumn i matrisen är en variabel. Variabler är egenskaper som vi mäter hos personerna. Kön, Ålder, Hälsa och Hästar är variabler.
Som du ser så kan vi beskriva variabler med ord eller siffror. Variabler som naturligt mäts på en numerisk skala kallas för kvantitativa variabler. Ålder och Hästar är kvantitativa variabler. Andra exempel på kvantitativa variabler är längd, vikt, priser, löner, temperatur, antalet poäng på ett prov eller inflationstakten.
Variabler som beskrivs med kategorier kallas för kvalitativa variabler. Kön och Hälsa är kvalitativa variabler. Andra exempel på kvalitativa variabler är yrke, religion, bostadskommun, ögonfärg eller trivsel på jobbet (dålig, okej, bra). I matrisen ovan har vi använt ord för att beskriva kategorierna, men vi kan också ge värden till de olika kategorierna. Exempelvis kunde vi ersätta “man” med värdet 0 och “kvinna” med värdet 1. Kön skulle ändå vara en kvalitativ variabel eftersom de valda värdena inte har någon kvantitativ betydelse.
Med generella beteckningar beskriver vi en datamatris så här:
| id | X | Y | Z |
|---|---|---|---|
| 1 | x₁ | y₁ | z₁ |
| 2 | x₂ | y₂ | z₂ |
| 3 | x₃ | y₃ | z₃ |
| 4 | x₄ | y₄ | z₄ |
| … | … | … | … |
| n | xₙ | yₙ | zₙ |
X, Y och Z betecknar variabler.
Den första observationen på X betecknas \(X_{1}\), den andra observationen \(X_{2}\), …, den sista observationen betecknas \(X_{n}\). n är alltså antalet observationer.
Vi kan också beteckna en observation på X med \(X_{i}\), men här har vi valt att inte specifikt ange dess ordning. \(X_{i}\) är helt enkelt den “i:te observationen”, där i kan vara 1, 2, 3, …, eller n.
2.2 Frekvensfördelningar
När vi matat in data i en datamatris så är de dags att se vad vi kan lära oss av materialet: Hur ser variablernas fördelningar ut? När vi beskriver en variabels fördelning så betyder det att vi visar hur den variabeln fördelar sig över olika värden på talaxeln, eller hur variabeln fördelar sig över olika kategorier. Eller med andra ord: Hur vanliga är olika värden i data? För att se detta kan vi använda frekvenstabeller och frekvensdiagram.
Frekvenstabeller
Nedan visas två frekvenstabeller som bygger på data från föregående avsnitt:
| Kön | Frekvens |
|---|---|
| Kvinna | 3 |
| Man | 3 |
Den här frekvenstabellen visar att tre kvinnor och tre män besvarade enkäten. Frekvens är allså ett annat ord för antal.
| Hästar | Frekvens |
|---|---|
| 2 | 2 |
| 3 | 1 |
| 4 | 1 |
| 5 | 2 |
Den här frekvenstabellen visar att 2 personer såg två hästar; 1 person såg tre hästar; 1 person såg fyra hästar och 2 personer såg fem hästar.
Nedan visas en frekvenstabell där vi också inkluderat en kumulativ frekvens och en relativ frekvens:
| Hästar | Frekvens | Kumulativ frekvens | Relativ frekvens |
|---|---|---|---|
| 2 | 2 | 2 | 1/3 |
| 3 | 1 | 3 | 1/6 |
| 4 | 1 | 4 | 1/6 |
| 5 | 2 | 6 | 1/3 |
Frekvenstabellen visar till exempel att 1 person såg tre hästar; den kumulativa frekvensen visar att 3 personer såg tre hästar eller färre. På samma sätt visar den kumulativa frekvensen att 6 personer såg fem hästar eller färre. En kumulativ frekvens visar alltså hur många personer som har ett visst värde på variabeln - eller ett lägre värde.
Relativ frekvens är ett annat ord för andel. Här ser vi exempelvis att en tredjedel av personerna såg två hästar, och att en sjättedel såg fyra hästar.
Inom statistiken brukar man också ofta uttrycka andelar i termer av odds. Det är därför användbart att veta vad ett odds egentligen mäter. I det här exemplet så skulle vi säga att 1/3 av personerna såg två hästar eller att oddset för att se två hästar är 0,5. Det betyder att det går 0,5 personer som såg två hästar på varje person som inte såg två hästar. Eller med andra ord: 2 personer såg två hästar och 4 personer såg inte två hästar. Detta ger oss ett odds på 2/4 = 0,5. På motsvarande sätt skulle vi säga att oddset för att vara kvinna är 1, dvs. det går en kvinna på varje man. Ett odds på 1 betyder alltså att det är 50/50. Och om oddset vore 10 så skulle det betyda att det går 10 kvinnor på varje man så att ungefär 90 procent är kvinnor.
När vi räknar ut en andel så tar vi kvoten mellan antalet “gynnsamma” utfall och totala antalet utfall. När vi räknar ut ett odds tar vi istället kvoten mellan antalet gynnsamma utfall och antalet ogynnsamma utfall:
\[andel = \frac{antal\ gynnsamma\ utfall}{totala\ antalet\ utfall}\] \[odds = \frac{antal\ gynnsamma\ utfall}{antal\ ogynnsamma\ utfall}\]
Frekvensdiagram
Vi har nu sett hur vi kan använda frekvenstabeller för att beskriva fördelningen för en variabel. Vi kan också beskriva samma information grafiskt med hjälp av frekvensdiagram:
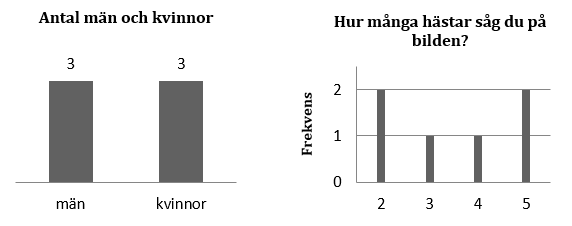
Ett frekvensdiagram är en figur som illustrerar en variabels fördelning. Vanligtvis sätter vi variabelns värden eller kategorier på x-axeln; y-axeln visar vanligtvis frekvensen (alternativt den kumulativa eller relativa frekvensen). I figuren till vänster är y-axeln “osynlig” men skulle vi rita ut den så skulle den visa frekvensen. Frekvensdiagram som görs upp för kvalitativa data kallas också för stapeldiagram; figuren uppe till vänster är ett stapeldiagram.
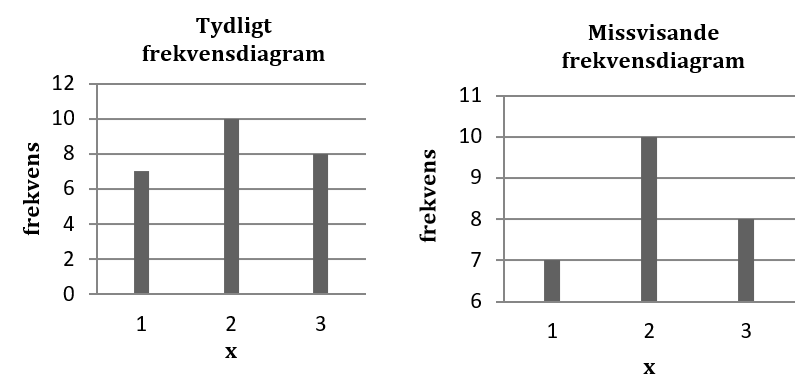
Finns det något man ska tänka på när man gör upp ett frekvensdiagram? Jo, här är en sak. x-axeln kan börja där det passar data bäst (här tänker vi oss att x-axeln visar variabelns värden). I frekvenstabellen uppe till höger så börjar x-axeln vid 1,5. Men y-axeln bör börja vid 0. Annars får man en förvrängd bild av datamaterialet, vilket figurerna nedan visar. I figuren till höger börjar y-axeln vid 6. Detta ger intrycket av att talet 2 är starkt överrepresenterat, fastän detta egentligen inte är fallet.
Exempel. Nedan visas livslängden i några av världens länder:
60,524; 77,185; 70,874; 51,498; 75,783 … 58,142
Totalt täcker samplet cirka 200 länder och om vi ritar upp datamaterialet i ett frekvensdiagram så får vi följande figur:
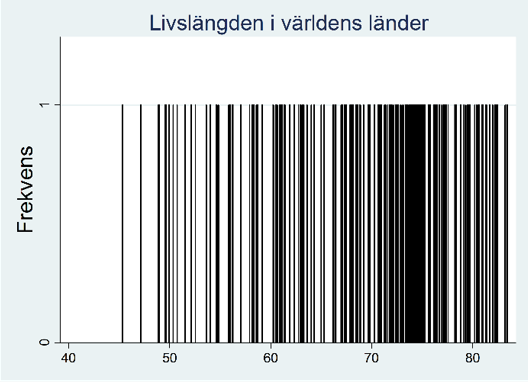
Det är svårt att få en bra bild av fördelningen utifrån den här figuren. Som vi nu ska se så kan man göra bilden klarare genom att först dela in data i grupper. Ett frekvensdiagram baserat på gruppindelat data kallas för ett histogram.
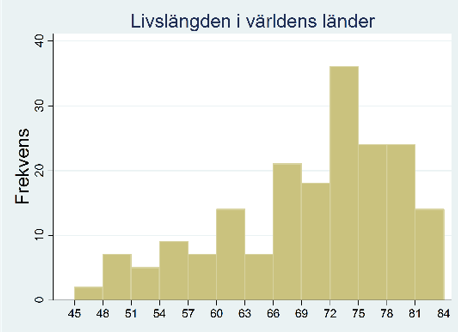
I figuren nedan har vi valt att dela in länderna i tretton grupper så att den första gruppen är länder med en livslängd på 45 till 48 år; den andra gruppen är länder med en livslängd på 48 till 51 år; …; den sista gruppen är länder med en livslängd på 81 till 84 år.
| Livslängd | Frekvens |
|---|---|
| 45,001-48 | 2 |
| 48,001-51 | 7 |
| 51,001-54 | 5 |
| 54,001-57 | 9 |
| 57,001-60 | 7 |
| ... | ... |
| 81,001-84 | 14 |
Typer av fördelningar och log-transformationen
Vissa typer av histogram dyker upp i så pass många olika sammanhang att det blir praktiskt att ge dem namn. Nedan ser du fem sådana fördelningar.
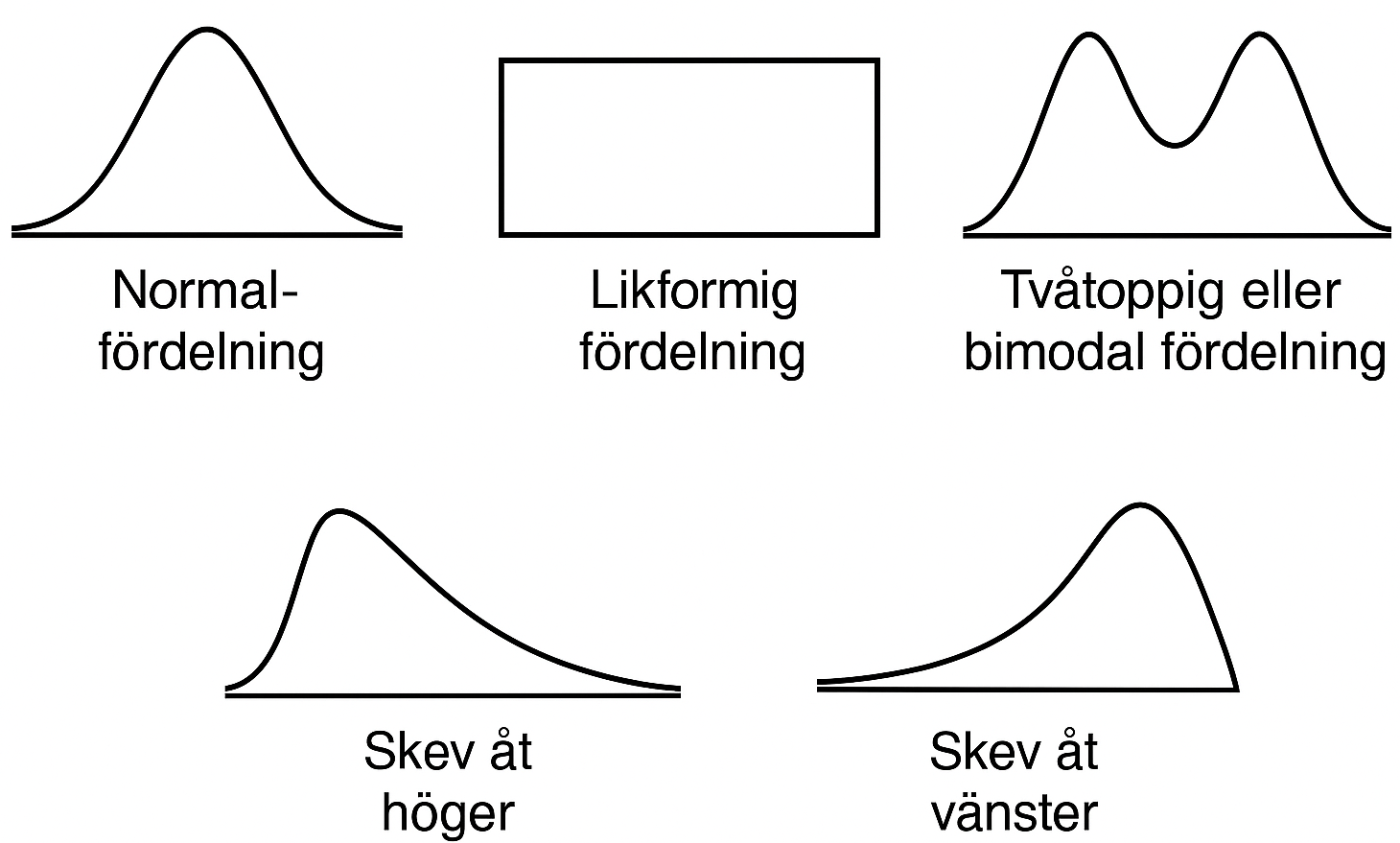
Uppe till vänster har vi en normalfördelning. Vi känner igen en normalfördelning på dess symmetriska och klockformade mönster. Normalfördelningen är den viktigaste fördelningen inom statistiken. En orsak är att många variabler följer en normalfördelning, åtminstone ungefärligt. Här är några exempel: Längden för en kvinna, barnets födelsevikt, blodtrycket hos en ung person och vilopulsen hos en frisk vuxen. Många tester konstrueras så att testpoängen ska följa en normalfördelning, exempelvis intelligenstester.
Den mittersta figuren på övre raden är ett exempel på en likformig fördelning, dvs. alla värden är lika vanliga. Längst till höger på samma rad har vi en bimodal fördelning som karaktäriseras av att den har två tydliga toppar.
Den vänstra figuren på nedre raden är ett exempel på en fördelning som är skev åt höger, dvs. den har en längre “svans” till höger. Om svansen istället ligger till vänster så säger vi att fördelningen är skev åt vänster.
Jämför nu en fördelning som är skev åt höger med en som är skev åt vänster. Vilken av dessa tror du att man stöter på mest i praktiken? De allra flesta som jobbar med data skulle nog svara “skev åt höger”. Så varför är den här typen av fördelningar så vanliga? En orsak är att många variabler är begränsade så att variabeln inte kan ha ett negativt värde, men däremot kan variabeln i princip ha hur stora värden som helst. Detta gäller inte minst sånt som mäts i pengar och kvantiteter (löner, omsättning, intäkter, antalet anställda på olika företag, …). Vissa personer tjänar då extra mycket i jämförelse med en typisk löntagare och vissa företag har extra många anställda i jämförelse med det typiska företaget – dessa skapar svansarna till höger.
Nedan ser du ett annat exempel på en fördelning som är skev åt höger. Detta histogram bygger på data för ca 10 000 amerikaner och visar deras BMI (body mass index: <18,5: underviktig; 18,5-24,9: normalviktig; >25: överviktig).
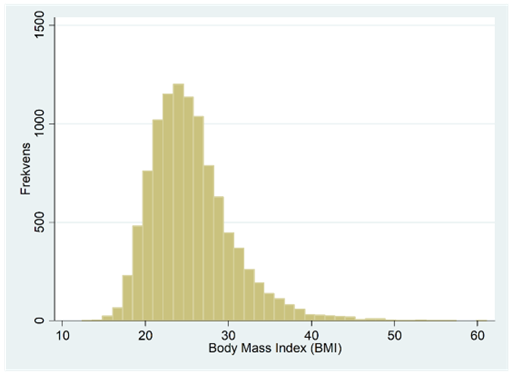
Om vi logaritmerar BMI-värdena så får vi histogrammet nedan, dvs. en normalfördelning. Vi säger då att BMI följer en lognormalfördelning. En lognormalfördelning karaktäriseras alltså av att den är skev åt höger och blir en normalfördelning efter logaritmering. Gemensamt för alla lognormalfördelningar är att variabeln (i detta exempel BMI) bara antar positiva värden.
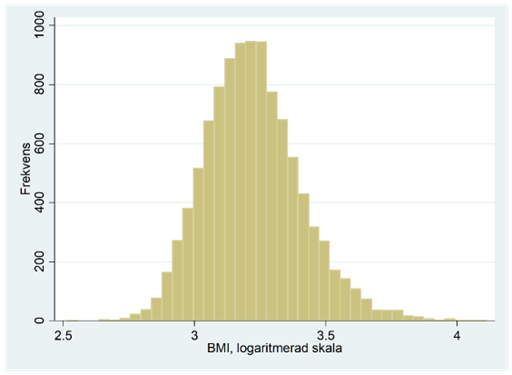
Inom statistiken är det vanligt att använda en logaritmerad skala för variabler som följer en fördelning som är skev åt höger. Det är därför bra att fundera lite på vad logaritmering innebär. Vi ser detta bäst genom ett exempel:
Låt oss säga att Adam fått en löneökning från 2000 till 2200 euro, och att Eva fått en löneökning från 4000 till 4400 euro. Uttryckt i euro har Evas lön ökat mer än Adams, men procentuellt sett så har båda fått en löneökning på 10%. Om vi nu mäter Adams och Evas löner på en logaritmisk skala så kommer vi att märka att bådas löner ökat lika mycket. Du kan testa detta med din miniräknare genom att slå in log(2200) – log(2000); du kommer att se att skillnaden blir lika stor som log(4400) – log(4000). Det här gäller oavsett om du använder en logaritm med basen 10 eller, exempelvis, den naturliga logaritmen. Den logaritmiska skalan “bryr sig” med andra ord om procentuella skillnader och inte absoluta: När ett värde ökar med en viss procent på den vanliga skalan, så är ökningen en viss konstant på den logaritmiska skalan.
Figuren nedan visar hur vi kan visualisera den logaritmiska skalan. På en logaritmisk skala är avståndet mellan 1 och 10 lika stort som det mellan 10 och 100: log(100)-log(10) = log(10)-log(1). På motsvarande sätt är avståndet mellan 1 och 2 lika stort som det mellan 2 och 4 och avståndet mellan 1 och 5 är lika stort som det mellan 5 och 25.
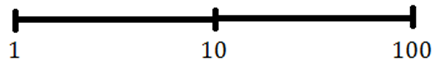
Vi kan nu se hur en fördelning med en längre svans till höger kan bli symmetrisk genom logaritmering. Nedan visas BMI-fördelningen. Procentuellt sett så gäller att avståndet mellan 20 och 30 är lika långt som avståndet mellan 30 och 45; båda gångerna ökar vi med 50 procent.
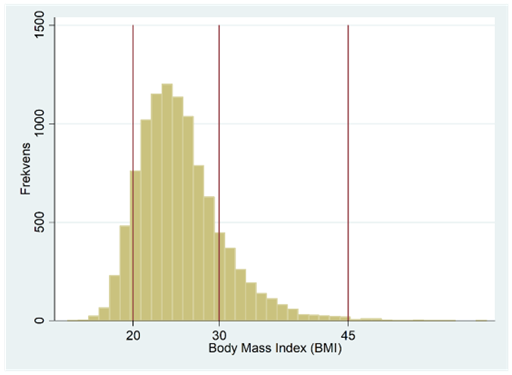
När vi logaritmerar värdena så pressar vi ihop skalan så att stora värden straffas extra hårt: Avståndet mellan 20 och 30 blir lika stort som det mellan 30 och 45:
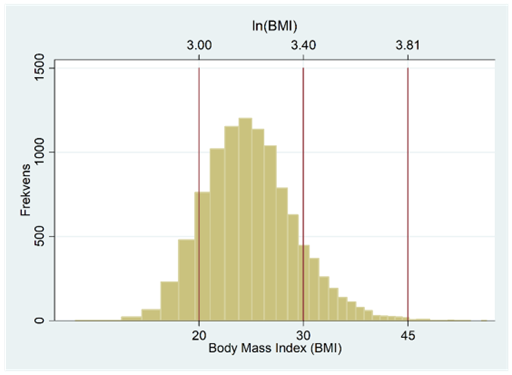
Men varför skulle man någonsin vilja logaritmera data istället för att beskriva det i originalform? Vi kommer bättre att se varför i kommande kapitel. I det här skedet ska vi bara introducera det som är en viktig del av förklaringen:
Den logaritmiska skalan stämmer ofta bättre överens med hur vi de facto ser på olika värden. Om priset på en bil stiger med 10 euro så skulle detta knappast spela någon roll för en bilköpare, men om priset på en schampoflaska stiger med 10 euro så skulle detta antagligen vara avgörande. Om Pelle får 50 000 euro mer i arvet efter sin mor än hans syster Anna, så skulle Anna knappast göra någon affär av detta om hon själv fick 5 miljoner euro, men däremot nog om hon bara fick 5000. De här exemplen visar att relativa skillnader ofta är viktigare än absoluta, och detta är exakt vad den logaritmiska skalan reflekterar.
Det finns flera logaritmer, t.ex. en logaritm med basen 10 eller den naturliga logaritmen. Inom statistiken är det vanligt att man använder den naturliga logaritmen som betecknas ln(…). Så varför är den här logaritmen så populär? Jo, för data får en naturlig förklaring när vi använder denna:
Anta att en aktie kostar 100 euro ena dagen och 101 euro andra dagen; det är en enprocentig ökning i priset. När vi tar den naturliga logaritmen av dessa priser och beräknar skillnaden så får vi värdet 0,01:
ln(101)-ln(100) \(\approx\) 0,01
Eller anta att en mäklare värderar ett hus till 100 000 euro men att huset säljs till 95 000 euro; det är en femprocentig minskning. Loggar vi priserna och tar skillnaden så får vi värdet -0,05:
ln(95000)-ln(100000) \(\approx\) -0,05
Lärdomen: När vi använder den naturliga logaritmen så representerar skillnaden mellan två loggade värden den procentuella skillnaden mellan värdena. Den här regeln fungerar bra då den procentuella skillnaden är liten (mindre än 10 procent) men blir mindre träffsäker för stora skillnader. Anta att aktien istället hade ökat i värde med 20 procent från 100 euro till 120. Den loggade skillnaden blir då ln(120)-ln(100) \(\approx\) 0,18 och inte 0,20. I kapitlets Appendix (A.1: Logaritmer) kan du läsa mer om logaritmer.
I det här avsnittet har vi sett att vi ibland kan beskriva en fördelning genom att ange vilken fördelningsfamilj den tillhör, såsom normalfördelningen eller lognormalfördelningen. Låt oss säga att vi mätt intelligenskvoten för 200 brottslingar. Om vi säger att brottslingarnas intelligenskvot är normalfördelad så ger detta en snabb bild av hur fördelningen ser ut. Däremot berättar detta inget om huruvida brottslingarna är dumma eller smarta, eller om det kanske finns stora skillnader i intelligens mellan en brottsling och en annan. Det är här läges- och spridningsmåtten kommer in. Lägesmåtten beskriver på lite olika sätt var på tallinjen vi hittar observationerna (“Är brottslingarna dumma eller smarta?”). Spridningsmåtten beskriver hur utspridda observationerna är över tallinjen (“Finns det stora skillnader i intelligens mellan en brottsling och en annan?”)
I kommande avsnitt ska vi se på några vanliga läges- och spridningsmått. När vi beskriver dem så använder vi ofta summatecknet, Σ. Första steget är därför att se vad det betyder.
2.3 Summatecknet, Σ
Vi använder summatecknet, Σ, för att beskriva en summa på ett kortfattat sätt. Anta att vi har gjort tre mätningar på en variabel X. Vi betecknar dem med x1, x2 och x3. Summan av observationerna kan vi beskriva som:
\[\sum_{\mathbf{i = 1}}^{\mathbf{3}}\mathbf{x}_{\mathbf{i}} = x_{1} + x_{2} + x_{3}\]
Här är ett konkret exempel: Anta att observationerna har värdena 1, 0 och 2. Summan blir då 3:
\[\sum_{\mathbf{i = 1}}^{\mathbf{3}}\mathbf{x}_{\mathbf{i}} = 1 + 0 + 2 = 3\]
Under summatecknet står det i = 1; ovanför summatecknet står det 3. Det här betyder att vi summerar från den första observationen till den tredje. Om samplet består av n stycken observationer så beskriver vi summan av dessa som:
\[\sum_{\mathbf{i = 1}}^{\mathbf{n}}\mathbf{x}_{\mathbf{i}} = x_{1} + x_{2} + \ldots + x_{n}\]
Ofta är det en självklarhet att vi summerar från den första observationen (1) till den sista (n). För enkelhetens skull kan vi därför lämna bort i = 1 och n och bara skriva:
\[\sum_{}^{}\mathbf{x}_{\mathbf{i}} = x_{1} + x_{2} + \ldots + x_{n}\]
Det är inte alltid som vi vill summera över observationerna i samplet; ibland vill vi summera över någon funktion av dessa observationer. Här är ett exempel där vi summerar över de kvadrerade värdena på x:
\[\sum_{}^{}\mathbf{x}_{\mathbf{i}}^{\mathbf{2}} = x_{1}^{2} + x_{2}^{2} + \ldots + x_{n}^{2}\]
För samplet (1, 0, 2) blir denna summa 5:
\[\sum_{}^{}\mathbf{x}_{\mathbf{i}}^{\mathbf{2}} = 1^{2} + 0^{2} + 2^{2} = 5\]
Vi kan jämföra detta med:
\[\left( \sum_{}^{}\mathbf{x}_{\mathbf{i}} \right)^{\mathbf{2}} = \left( x_{1} + x_{2} + x_{3} \right)^{2} = (1 + 0 + 2)^{2} = 9\]
Summan nedan beskriver att vi summerar över en skillnad – skillnaden mellan en observation och värdet 1:
\[\sum_{}^{}{\left( x_{i} - 1 \right) = \left( x_{1} - 1 \right)} + \left( x_{2} - 1 \right) + \ldots + \left( x_{n} - 1 \right)\]
För samplet (1, 0, 2) så blir denna summa 0:
\[ \sum_{i=1}^3 (x_i - 1) = \underbrace{(x_1 - 1)}_{=\,1-1} + \underbrace{(x_2 - 1)}_{=\,0-1} + \underbrace{(x_3 - 1)}_{=\,2-1} = 0 \]
Vi kan jämföra detta med:
\[\sum_{}^{}{x_{i} - 1} = x_{1} + x_{2} + x_{3} - 1 = 1 + 0 + 2 - 1 = 2\]
2.4 Lägesmått
Lägesmåtten beskriver var på tallinjen vi hittar observationerna i ett sampel. De viktigaste lägesmåtten är medelvärdet och medianen. Andra vanliga lägesmått är typvärdet, kvartiler och percentiler.
Medelvärdet
Medelvärdet beräknas som summan av observationerna delat med antalet observationer. Om vi mäter medelvärdet för en variabel som betecknas x så betecknar vi medelvärdet med \(\overline{x}\):
\[\overline{x} = \frac{\sum_{}^{}x_{i}}{n} = \frac{x_{1} + x_{2} + \ldots + x_{n}}{n}\]
Exempel. I samplet nedan så är genomsnittsåldern 41 år. Vi får medelvärdet genom att ta summan av alla åldrar (246) och dela med antalet personer (6). På motsvarande sätt kan vi räkna ut att personerna i genomsnitt såg 3,5 hästar.
| ID | Kön | Ålder | Hälsa | Hästar |
|---|---|---|---|---|
| 1 | Man | 32 | God | 5 |
| 2 | Kvinna | 48 | Utmärkt | 4 |
| 3 | Kvinna | 20 | God | 5 |
| 4 | Kvinna | 66 | Ganska svag | 3 |
| 5 | Man | 45 | Mycket svag | 2 |
| 6 | Man | 35 | Utmärkt | 2 |
Men hur tolkar vi medelvärdet? Vad betyder det när vi säger att genomsnittsåldern är 41 år? Här är två tolkningar:
- Om vi ser på observationerna som tyngder på en våg så är medelvärdet den axel som gör att vågen balanserar exakt:
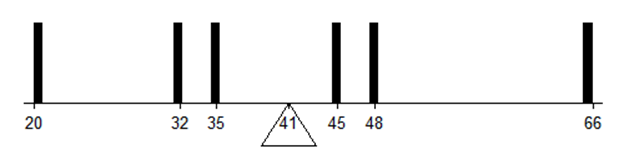
- Medelvärdet brukar ses som den bästa gissningen. Eleverna i klass 6a på St. Henriks lågstadium bor i genomsnitt två kilometer från skolan. Pelle går på den här klassen. Hur lång är hans skolväg? Utan någon annan information så är “två kilometer” din bästa gissning. Vissa på klassen bor närmare skolan, andra bor längre ifrån, men sett över alla personer så tar dessa fel ut varandra; medelvärdet har rätt i genomsnitt.
Exempel. Hur är det då med variabeln kön: Kan vi räkna ut medelvärdet för kön? I så fall måste vi först sätta värden på variablernas kategorier. Låt oss ge männen värdet 0 och kvinnorna värdet 1:
| ID | Kön | Ålder | Hälsa | Hästar |
|---|---|---|---|---|
| 1 | Man = 0 | 32 | God | 5 |
| 2 | Kvinna = 1 | 48 | Utmärkt | 4 |
| 3 | Kvinna = 1 | 20 | God | 5 |
| 4 | Kvinna = 1 | 66 | Ganska svag | 3 |
| 5 | Man = 0 | 45 | Mycket svag | 2 |
| 6 | Man = 0 | 35 | Utmärkt | 2 |
Medelvärdet blir då 0,5: \(\frac{0 + 1 + 1 + 1 + 0 + 0}{6} = 0,5\). Medelvärdet är andelen kvinnor i samplet.
Det här gäller alltid: Om vi räknar ut medelvärdet för en variabel som bara antar två värden – 0 och 1 – så är medelvärdet andelen 1:or i samplet. Av den här orsaken brukar man ofta använda just siffrorna 0 och 1 för variabler med bara två kategorier. Vi kallar den här typen av variabler för binära. Man brukar ofta namnge binära variabler enligt kategorin som har värdet 1:
Istället för att kalla en variabel för “kön” så kan vi kalla den för “kvinna” om kvinnor har värdet 1 och män värdet 0. Istället för att kalla en variabel för “modersmål” så kan vi kalla den för “svenska” om personer med svenska som modersmål har värdet 1 och personer med finska som modersmål har värdet 0. Istället för att kalla en variabel för “utbildningskategori” så kan vi kalla den för “högutbildad” om högutbildade har värdet 1 och de lågutbildade har värdet 0.
Exempel. Hur är det då med variabeln hälsa? Kan vi räkna ut medelvärdet för den variabeln? Rent tekniskt sett så är det förstås möjligt om vi ger värden till de olika kategorierna. Men ett sådant medelvärde har ingen meningsfull betydelse. Medelvärdet beror då på hur vi väljer att koda variabeln, och valet är godtyckligt.
Medianen
Vi inledde det här kapitlet med att säga att medelvärdet hör till de viktigaste lägesmåtten. Men när har vi intresse av andra lägesmått? För att se detta så ska vi fundera över följande:
I USA ligger den genomsnittliga årsinkomsten kring 40 600 dollar, men 65 procent av befolkningen tjänar mindre än detta. Det här kan låta paradoxalt men är sant, dvs. en majoritet kan ligga under snittet. Det kan då vara intressantare att fundera över hur mycket en representativ person tjänar. Det är här medianen kommer in: Medianen är den mittersta observationen i samplet.
Exempel. Fem kompisar går ut och äter tillsammans. Här är notan för varje person då vi ordnat dem från den som betalade minst till den som betalade mest:
16, 20, 25, 33, 35
Medianen är 25 euro, eftersom 25 är det mittersta värdet.
Exempel. Hur stor är medianåldern?
| ID | Kön | Ålder | Hälsa | Hästar |
|---|---|---|---|---|
| 1 | 0 | 32 | God | 5 |
| 2 | 1 | 48 | Utmärkt | 4 |
| 3 | 1 | 20 | God | 5 |
| 4 | 1 | 66 | Ganska svag | 3 |
| 5 | 0 | 45 | Mycket svag | 2 |
| 6 | 0 | 35 | Utmärkt | 2 |
Då vi rangordnar observationerna från den minsta till den största så får vi:
20, 32, 35, 45, 48, 66
Två åldrar – 35 och 45 – ligger lika mycket på mitten. Medianen blir då snittet av dessa två, dvs. (35+45)/2 = 40. På motsvarande sätt kan vi räkna ut att medianen för variabeln hästar är 3,5.
För det här samplet är genomsnittsåldern 41 år; medianen är 40. Personerna såg 3,5 hästar i genomsnitt och medianen är också 3,5. Det är inte ovanligt att medelvärdet och medianen har ungefär samma värden. Så på vilket sätt skiljer sig de här måtten från varandra? Det finns tre tillfällen då skillnaderna blir extra tydliga:
- Medelvärdet är känsligt inför extrema värden, så kallade outliers.
Tänk dig följande sampel: 1, 2, 3, 4 och 5. Både medelvärdet och medianen har värdet 3. Men vad händer om värdet 5 plötsligt ändrar till 1000? Jo, medelvärdet ökar dramatiskt, men medianen är fortfarande 3.
- Medelvärdet och medianen har olika värden i skeva fördelningar.
Figur A visar fördelningen för inkomst per person i världens länder. Man säger att den här fördelningen är skev åt höger; det finns en del länder där inkomsterna är betydligt högre än i andra länder – dessa skapar fördelningens högra svans. I ett genomsnittligt land är inkomsten ungefär 12600 dollar per person men medianen är bara 7000 dollar; medelvärdet dras upp av de höga inkomsterna i fördelningens högra svans.
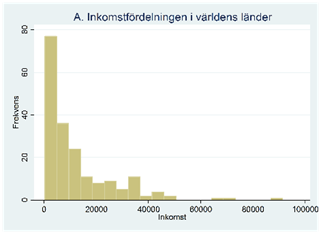
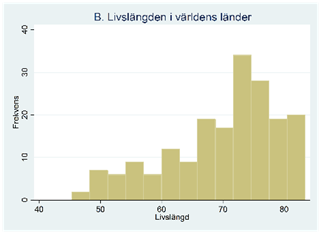
Figur B visar fördelningen för livslängden i världens länder. Man säger att den här fördelningen är skev åt vänster. I ett genomsnittligt land är livslängden 70,0 år men medianen är 72,5 år; medelvärdet dras ner av de korta livslängderna i fördelningens vänstra svans.
- Vi kan beräkna medelvärdet för kvantitativa och binära data (0/1). Medianen är dessutom lämplig för data på ordinalnivå.
Exempel. Kan vi räkna ut medianen för variabeln hälsa? För att göra detta så måste vi först ge värden till de olika kategorierna. Låt oss ge “mycket svag hälsa” värdet 1; “Ganska svag hälsa” värdet 2; “god hälsa” värdet 3 och “utmärkt hälsa” värdet 4:
| ID | Kön | Ålder | Hälsa | Hästar |
|---|---|---|---|---|
| 1 | 0 | 32 | God = 3 | 5 |
| 2 | 1 | 48 | Utmärkt = 4 | 4 |
| 3 | 1 | 20 | God = 3 | 5 |
| 4 | 1 | 66 | Ganska svag = 2 | 3 |
| 5 | 0 | 45 | Mycket svag = 1 | 2 |
| 6 | 0 | 35 | Utmärkt = 4 | 2 |
Medianen blir då 3, vilket representerar “god hälsa”.
Det här värdet är naturligtvis godtyckligt; om vi hade valt att koda hälsokategorierna på ett annat sätt så hade vi fått en annan median. Vi hade exempelvis kunnat ge “mycket svag hälsa” värdet -10; “ganska svag hälsa” värdet -5; “god hälsa” värdet 0 och “utmärkt hälsa” värdet 10. Då hade medianen blivit 0. Men notera här att den fortfarande representerar kategorin “god hälsa”. Det här innebär att medianen i praktiken inte påverkas av hur vi kodar variabeln så länge kodningen beaktar hälsokategoriernas rangordning. Det är därför meningsfullt att beräkna medianen för variabeln hälsa – trots att den är en kvalitativ variabel.
Hälsa är ett exempel på en variabel med data på ordinalnivå. Ordinalnivå är kvalitativa data där det finns en naturlig rangordning av kategorierna: utmärkt hälsa \(\succ\) god hälsa \(\succ\) svag hälsa \(\succ\) mycket svag hälsa. Vi kan representera den här rangordningen med siffror (t.ex. 4-3-2-1) men skillnaden mellan olika värden har ingen kvantitativ betydelse. Exempel: Om Pelle har en hälsa på 4 och Lisa en hälsa på 3 så visar detta att Pelle har bättre hälsa än Lisa, men inte hur mycket bättre. Kvalitativa variabler där kategorierna inte kan rangordnas på ett meningsfullt sätt har data på nominalnivå.
Här är några exempel: Din lön mäts på en kvantitativ skala – din socioekonomiska ställning (låg, medel, hög) mäts på ordinalnivå. Din hårlängd (i centimeter) mäts på en kvantitativ skala – din hårfärg mäts på nominalnivå. Försäljningspriset för en bil mäts på en kvantitativ skala – bilens märke mäts på nominalnivå. Sockerhalten i en semla mäts på en kvantitativ skala – den upplevda sötman (säg på en skala mellan 1 och 5) mäts på ordinalnivå.
Det finns också gråzoner i skarvet mellan ordinalnivå och kvantitativa data. Detta gäller bland annat olika index och poäng som ges till personer i psykologiska tester. Om man, exempelvis, vill mäta hur extrovert en person är så kan man göra detta genom att låta personen ta ställning till ett antal frågor (se figuren nedan). Svaren poängsätts och summeras ihop och bildar en så kallad likert-skala. Eller om man vill mäta hur demokratiskt ett land är kan man värdera detta utifrån ett antal faktorer och skapa ett index. Den här typen av data kan betraktas som ordinalnivå eftersom “extroversion” eller “graden av demokrati” inte naturligt mäts på numeriska skalor. Ofta behandlar man ändå den här typen av data som kvantitativt, genom att exempelvis beräkna medelvärden.

Typvärdet
Typvärdet är det värde som förekommer flest gånger i samplet. Om flera värden är lika vanliga så kan det finnas flera typvärden.
Exempel. Typvärdena för variabeln hästar är 2 och 5.
| ID | Kön | Ålder | Hälsa | Hästar |
|---|---|---|---|---|
| 1 | 0 | 32 | 3 | 5 |
| 2 | 1 | 48 | 4 | 4 |
| 3 | 1 | 20 | 3 | 5 |
| 4 | 1 | 66 | 2 | 3 |
| 5 | 0 | 45 | 1 | 2 |
| 6 | 0 | 35 | 4 | 2 |
Kvartiler och låddiagram
Figuren nedan illustrerar vad vi menar med kvartiler. Lådan representerar ett datamaterial som vi rangordnat och delat upp i fyra jämnstora delar. Vi får då tre skarvar som vi betecknar med Q1, Q2 och Q3 – detta är datamaterialets kvartiler.
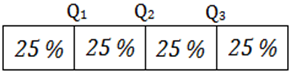
Den första kvartilen (Q1) är en observation som är större än en fjärdedel av observationerna och mindre än tre fjärdedelar.
Den andra kvartilen (Q2) är en observation som är större än hälften av observationerna och mindre än hälften. (Den andra kvartilen och medianen är samma mått.)
Den tredje kvartilen (Q3) är en observation som är större än tre fjärdedelar av observationerna och mindre än en fjärdedel.
Låt oss säga att vi mäter lönerna för ett sampel ungdomar på sitt första sommarjobb. Om den första lönekvartilen är 7 euro per timme så betyder det att en fjärdedel av ungdomarna tjänar mindre än 7 euro och tre fjärdedelar mer. Om den tredje lönekvartilen är 10 euro per timme så betyder det att tre fjärdedelar tjänar mindre än 10 euro och en fjärdedel mer.
För att illustrera kvartilerna kan man använda något som kallas för ett låddiagram. Här har vi gjort upp ett låddiagram för livslängden i världens länder:
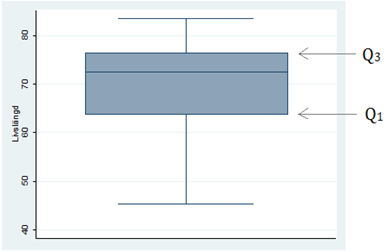
Lådans botten är den första kvartilen som här har värdet 64; en fjärdedel av länderna har en livslängd som är kortare än 64 år och tre fjärdedelar en livslängd som är längre. Lådans tak är den tredje kvartilen som här har värdet 76; tre fjärdedelar av länderna har en livslängd som är kortare än 76 år. Inom lådan ryms med andra ord 50 procent av världens länder – de mittersta 50 procenten. Lådans mittstreck är medianen.
Om vi räknar ut lådans längd så ser vi att den är 12 år (76 - 64 = 12). Vi kallar detta avstånd för kvartilavståndet.
Förutom lådan så innehåller låddiagrammet också en gaffel som märker ut datamaterialets största och minsta observationer. Om datamaterialet innehåller en eller flera outliers (extra stora eller små värden) så märks dessa också ut skilt, som i figuren nedan:
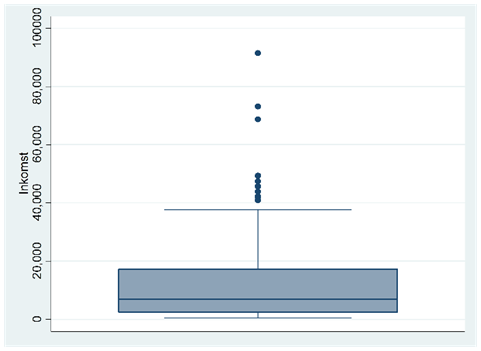
(För låddiagram brukar man definiera en outlier som en observation som ligger minst 1,5 lådor under lådans nedre kant, eller 1,5 lådor ovanför den övre.)
Deciler och percentiler
Vi får decilerna genom att dela in data i tio jämnstora grupper:
Det här betyder att det finns totalt nio deciler (de nio skarvarna i figuren ovan). Exempel: Fyra tiondelar av observationerna är mindre än den fjärde decilen; sex tiondelar är större.
Ibland talar man också om decilgrupper. Exempel: Vi mäter inkomst per person i världens länder. Om Angola hör till den första decilgruppen så betyder det att Angola hör till de tio procent fattigaste länderna i världen. Notera att det bara finns nio deciler, men tio decilgrupper.
På motsvarande sätt får vi percentilerna genom att dela in data i 100 jämnstora grupper. Exempel: Den 90:e percentilen är en observation som är större än 90 procent av observationerna men mindre än 10 procent. När vi mäter inkomst per person i världens länder så är den 90:e percentilen 34 132 dollar. Det betyder att inkomsten per person än lägre än 34 132 dollar i 90 procent av länderna, och högre i tio procent.
2.5 Spridningsmått
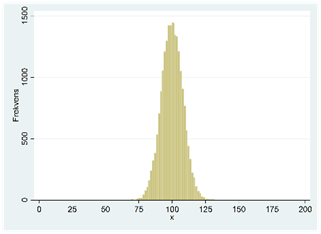
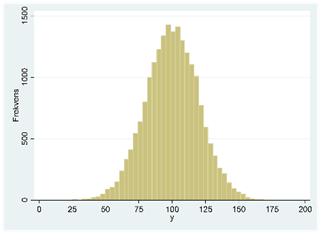
Nedan visas två histogram. Båda fördelningarna har samma medelvärde och median. Det finns dock en viktig skillnad mellan fördelningarna: spridningen. I figuren till vänster ligger observationerna relativt nära varandra; i figuren till höger finns det betydligt större skillnader mellan observationerna. I det här avsnittet ska vi lära oss hur vi kan beskriva den här egenskapen hos en fördelning. De viktigaste måtten är variansen och standardavvikelsen.
Variansen och standardavvikelsen
Hur skulle man gå tillväga för att beskriva spridningen för en variabel? En naturlig utgångspunkt är att se hur mycket observationerna varierar kring medelvärdet; tenderar observationerna ligga tajt samlade kring medelvärdet eller långt från medelvärdet? Variansen och standardavvikelsen är två mått som bygger på den tanken.
Variansen mäter ungefär den genomsnittliga kvadrerade avvikelsen mellan en observation och medelvärdet. Vi betecknar variansen med s2:
\[s^{2} = \frac{\sum_{}^{}\left( x_{i} - \overline{x} \right)^{2}}{n - 1} = \frac{\left( x_{1} - \overline{x} \right)^{2} + \left( x_{2} - \overline{x} \right)^{2} + \ldots + \left( x_{n} - \overline{x} \right)^{2}}{n - 1}\]
Standardavvikelsen är den positiva kvadratroten ur variansen. Vi betecknar den med s:
\[s = \sqrt{s^{2}}\]
Exempel. Vi gör tre mätningar på en variabel X och får värdena: 2, 1, 3. Hur stor är variansen och standardavvikelsen?
Medelvärdet är 2. Summan av de kvadrerade avvikelserna blir då 2:
\[\sum_{}^{}\left( x_{i} - \overline{x} \right)^{2} = {(2 - 2)}^{2} + {(1 - 2)}^{2} + {(3 - 2)}^{2} = 2\]
Vi får sedan variansen genom att dela kvadratsumman (2) med antalet observationer minus ett (3-1 = 2). Variansen blir då 1:
\[s^{2} = \frac{2}{2} = 1\]
Standardavvikelsen blir därför också 1:
\[s = \sqrt{1} = 1\]
Notera här vad som skulle hända om vi inte kvadrerade: En positiv avvikelse (3-2) skulle tas ut av en negativ (1-2) och summan skulle bli noll. Detta gäller i alla datamaterial, dvs. om man summerar ihop alla observationers avvikelser från medelvärdet så blir summan alltid 0.
Exempel. Hur stor är åldersvariansen?
När vi har lite större datamaterial kan det ta tid att räkna ut variansen för hand. En formel som gör uppgiften lite snabbare ges nedan:
\[s^{2} = \frac{\sum_{}^{}\left( x_{i} - \overline{x} \right)^{2}}{n - 1} = \frac{\sum_{}^{}x_{i}^{2} - n{\overline{x}}^{2}}{n - 1}\]
Vi börjar med att räkna ut summan av de kvadrerade åldrarna, \(\sum_{}^{}x_{i}^{2}\). Exempelvis är den första personen 32 år och 322 = 1024. Summan av alla kvadrerade åldrar är 11334:
| ID | Ålder | Ålder2 |
|---|---|---|
| 1 | 32 | 1024 |
| 2 | 48 | 2304 |
| 3 | 20 | 400 |
| 4 | 66 | 4356 |
| 5 | 45 | 2025 |
| 6 | 35 | 1225 |
| Σ = 11334 |
Medelåldern är 41 år och åldersvariansen blir då 249,6:
\[s^{2} = \frac{\sum_{}^{}x_{i}^{2} - n {\overline{x}}^{2}}{n - 1} = \frac{11334 - 6 \times 41^{2}}{6 - 1} = 249,6\]
Standardavvikelsen är då 15,8: \(\sqrt{249,6} \approx 15,8\)
Vi såg just att standardavvikelsen för ålder är cirka 16 år. Men vad betyder det? Generellt gäller att en stor standardavvikelse betyder att det är stor spridning i data; en liten standardavvikelse att spridningen är liten. En standardavvikelse på noll betyder att det inte finns någon variation alls, dvs. alla observationer i data har exakt samma värde. Negativa standardavvikelser finns inte. En standardavvikelse på 16 betyder ungefär att en genomsnittlig person i samplet har en ålder som ligger 16 år från snittet. Det är, så att säga, standard att ligga 16 år från snittet.
För att lära oss mer om variansen och standardavvikelsen så ska vi ännu se på tre egenskaper hos dessa:
- Om vi flyttar en fördelning på tallinjen så förändras inte variansen eller standardavvikelsen.
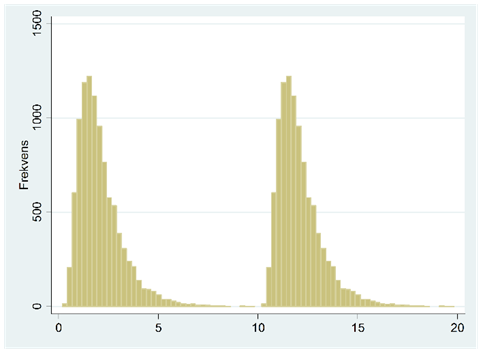
I figuren nedan har vi två fördelningar; i den vänstra har vi originalet och i den högra har vi adderat till 10 till varje observation. Som vi ser så förändrar detta inte spridningen i data. Variansen eller standardavvikelsen påverkas därför inte heller.
- Standardavvikelsen mäts i samma enhet som variabeln.
Anta att kvinnor i genomsnitt är 168 centimeter med standardavvikelsen 5 centimeter. Uttryckt i meter så är kvinnor i snitt 1,68 meter med standardavvikelsen 0,05 meter. Standardavvikelsen uttrycks alltså i samma enhet som variabeln ifråga (här centimeter och meter). Detta gäller dock inte variansen. Om kvinnor i snitt är 1,68 meter med standardavvikelsen 0,05 meter så är variansen 0,0025 kvadratmeter. Av den här orsaken är det populärare att rapportera standardavvikelsen i olika undersökningar.
- 95-100-regeln: För normalfördelade variabler gäller att ungefär 95 procent av observationerna ryms inom \(\pm\) två standardavvikelser från snittet, och så gott som 100 procent ryms inom \(\pm\) tre standardavvikelser från snittet.
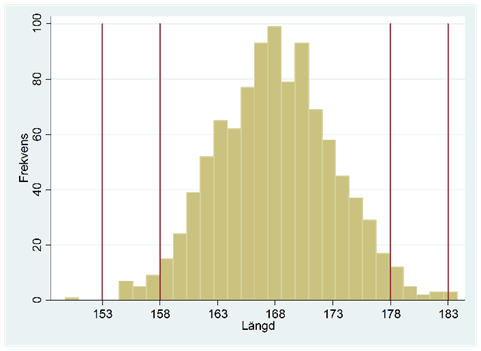
Anta att längden för en kvinna är normalfördelad. Om kvinnor i snitt är 168 centimeter med standardavvikelsen 5 centimeter så betyder det att ungefär 95 procent av kvinnor är mellan 158 och 178 centimeter (se figuren nedan). Och nästan alla kvinnor är mellan 153 och 183 centimeter; 153 ligger tre standardavvikelser under snittet och 183 tre standardavvikelser över.
Man kan undra varför vi delar med n-1 (och inte n) när vi beräknar variansen och standardavvikelsen. Det finns naturligtvis en förklaring, men här lämnar vi den till kapitlets Appendix (A.2 Variansen: Varför dela med n-1?).
Sammanfattning
Appendix
A.1 Logaritmer
Vad menas med en logaritm med basen 10? Se tabellen nedan. På den vanliga skalan ökar värdena med en faktor på 10 för varje rad; på den logaritmiska skalan ökar värdena med talet ett på varje rad. Vi kallar detta för en logaritm med basen 10. Exempelvis ser vi att log(100) = 2. Det betyder att vi måste ta 10 upphöjt i 2 för att få värdet 100. På samma sätt ser vi att log(1000) = 3: Vi måste ta 10 upphöjt i 3 för att få värdet 1000. När vi ställer oss frågan: “Vad är logaritmen av 1000?” så är det med andra ord bara ett kortare sätt att fråga: “Vad ska jag ta 10 upphöjt i för att få 1000”?
| Vanlig skala | Log10-skala |
|---|---|
| 1 | 0 |
| 10 | 1 |
| 100 | 2 |
| 1000 | 3 |
| 10 000 | 4 |
| … | … |
Inom statistiken är det vanligt att man använder en logaritm med basen e, där e är ett tal som har värdet 2,718… . Den här logaritmen kallas för den naturliga logaritmen och betecknas ln(…). Då ett värde ökar med en faktor e \(\approx\) 2,72 på den vanliga skalan så är ökningen ett på ln-skalan:
| Vanlig skala | ln-skala |
|---|---|
| 1 | 0 |
| e ≈ 2,72 | 1 |
| e \(\times\) e ≈ 7,39 | 2 |
| e \(\times\) e \(\times\) e ≈ 20,09 | 3 |
| e \(\times\) e \(\times\) e \(\times\) e ≈ 54,60 | 4 |
| … | … |
När vi ställer oss frågan: “Vad är den naturliga logaritmen av 10” så är det alltså bara ett kortare sätt att fråga: “Vad ska jag ta talet e upphöjt i för att få värdet 10?”.
Vi såg tidigare att ln(101) – ln(100) \(\approx\) 0,01 och att detta visar att 101 är en procent mer än 100. Men varför blir det så när vi tar den naturliga logaritmen?
När ett tal ökar med en faktor \(e \approx 2,72\) (dvs. 172 procent) på den vanliga skalan så är ökningen 1 på den naturliga logaritm-skalan.
Det går cirka 100 stycken 1-procentiga ökningar på en 172-procentig ökning.
När ett tal ökar med en procent på den vanliga skalan så är ökningen 1/100 = 0,01 på den naturliga logaritm-skalan.
A.2 Variansen: Varför dela med n-1?
Ett bra variationsmått ska mäta variationen i data och inget annat. Vi vill exempelvis inte att variationsmåttet beror av sampelstorleken. Anta exempelvis att vi vill jämföra lönespridningen bland lärare och tandläkare, och att lönespridningen egentligen är lika stor i båda grupperna. Vårt datamaterial består av enbart tio tandläkare men hundratals lärare. För att kunna jämföra yrkesgrupperna är det då viktigt att vi har ett spridningsmått som inte beror av sampelstorleken. Variationsvidden är ett exempel på ett variationsmått som inte uppfyller det kravet. Variationsvidden är skillnaden mellan den största observationen i data och den minsta. Ju större sampel desto större tenderar maxlönen bli och tvärtom för den minsta lönen; variationsvidden ökar alltså med sampelstorleken. I en jämförelse av lärarna och tandläkarna så skulle vi då felaktigt dra slutsatsen att lärarna har mer varierade löner än tandläkarna, då en korrekt slutsats vore att samplet är större för lärarna än tandläkarna.
Så varför delar vi med n-1 när vi beräknar variansen? Jo, när vi beräknar variansen genom att dela med n-1 så ser vi till att variansen inte beror av samplets storlek. Men om vi istället beräknar variansen genom att dela med n så tenderar variansen bli lite mindre i små sampel än i stora. Det är inte särskilt lätt att direkt se förklaringen. Men tänk så här: Variansen mäter ju hur mycket observationerna varierar kring medelvärdet. Och medelvärdet är det “balanserande värdet”. I ett litet datamaterial så måste medelvärdet bara balansera mellan ett fåtal observationer och får på så vis chansen att i snitt ligga lite närmare dessa observationer, än i ett stort datamaterial. Men den här effekten kan vi uppväga genom att dela med n-1.
Det är bra att variansen (när vi delar med n-1) inte varierar med samplets storlek, men det här är inte heller hela förklaringen till denna praxis. Orsaken till att vi delar med n-1 är att variansen då får en bra egenskap som kallas för väntevärdesriktighet. I det här skedet ska vi inte gå närmare in på det begreppet, men väntevärdesriktighet implicerar, bland annat, just det här – att variansen inte varierar systematiskt med datamaterialets storlek.
Övningsuppgifter
Datamatrisen
- Datamatrisen nedan visar ett utdrag av ett datamaterial för USA:s 50 stater.
| Stat | Befolkningsmängd (miljoner) | Procent män | Inkomst | Marijuana lagligt? |
|---|---|---|---|---|
| 1 Kalifornien | 38.8 | 49.7 | 43104 | 0 |
| 2 Texas | 27 | 49.6 | 39493 | 0 |
| 3 Florida | 19.9 | 48.9 | 39272 | 0 |
| 4 New York | 19.7 | 48.4 | 48821 | 0 |
| 5 Illinois | 12.9 | 49 | 43159 | 0 |
| 6 Alaska | 0.7 | 52 | 44174 | 1 |
| ... | ... | ..., | ... | ... |
| 50 Wyoming | 0.6 | 51 | 47851 | 0 |
Vad är observationsenheten?
Hur stort är antalet observationer?
Hur många kvantitativa variabler finns det och vilka är de?
Hur många kvalitativa variabler finns det och vilka är de?
Frekvensfördelningar
- Nedan visas ett sampel för 22 barn. För varje barn har vi mätt åldern då de lärde sig gå. Åldern är uttryckt i månader:
17, 17, 15, 15, 16, 14, 14, 16, 16, 13, 15, 16, 14, 18, 13, 15, 11, 13, 15, 15, 15, 16
- Beskriv åldersfördelningen genom att fylla i frekvenstabellen:
| Ålder | Frekvens |
|---|---|
| 11 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 |
- Illustrera åldersfördelningen med hjälp av ett frekvensdiagram.
- I en kommun gick 800 elever ut nian förra våren. Nedan ges en (ofullständig) frekvenstabell över elevernas slutbetyg i modersmål. Fyll i frekvensen och den relativa frekvensen. Hur stort är oddset för betyget 10?
| Betyg | Frekvens | Kumulativ frekvens | Relativ frekvens |
|---|---|---|---|
| 4 | 26 | ||
| 5 | 66 | ||
| 6 | 152 | ||
| 7 | 384 | ||
| 8 | 622 | ||
| 9 | 752 | ||
| 10 | 800 |
- 300 pensionärer får genomgå ett test där man mäter deras reaktionsförmåga i trafiken. Histogrammet nedan visar fördelningen för pensionärernas loggade reaktionstider (den naturliga logaritmen). Agnes (A) fick en reaktionstid som var hälften av Bosses (B).
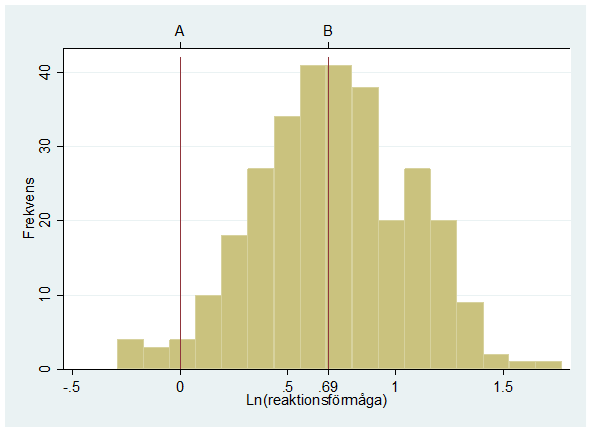
Calle hade dubbelt längre reaktionstid än Bosse. Märk ut Calles loggade reaktionstid i histogrammet. Skriv också ut värdet för Calles loggade reaktionsförmåga på x-axeln.
Dan hade 10 procent längre reaktionstid än Bosse. Vad är Dans reaktionstid mätt på den naturliga logaritm-skalan?
Mätt på den naturliga logaritm-skalan så ligger Evas reaktionstid 0,05 enheter under Bosses. Hur mycket snabbare är Eva än Bosse uttryckt i procent?
Summatecknet, Σ
- Vi gör fyra mätningar på en variabel X: 1, 2, 3, 6. Beräkna följande summor:
\(\sum_{}^{}x_{i}\)
\(\sum_{}^{}x_{i} - 3\)
\(\sum_{}^{}\left( x_{i} - 3 \right)\)
\(\sum_{}^{}\left( x_{i} - 3 \right)^{2}\)
\(\sum_{}^{}{2x_{i}}\)
\(2\sum_{}^{}x_{i}\)
- Vi gör 4 mätningar på en variabel X: -1, 0, 4, 5. Beräkna följande summor:
\(\sum_{}^{}x_{i}^{2}\)
\(\left( \sum_{}^{}x_{i} \right)^{2}\)
- Vi gör 500 mätningar på en variabel X. Summan av dessa är 2636. Beräkna:
\(\sum_{}^{}{2x_{i}}\)
\(\sum_{}^{}\left( x_{i} + 1 \right)\)
\(\sum_{}^{}\left( x_{i} - 2 \right)\)
Lägesmått
- Ett antal studier har visat att det är svårt att bibehålla en viktnedgång i långa loppet. En anledning kan vara att kroppens kaloribehov minskar då man går ner i vikt. Nedan visas data för tio personer, hämtat ur artikeln Effects of Dietary Composition on Energy Expenditure During Weight-Loss Maintenance. Här har man mätt skillnaden mellan en persons kaloribehov före en viktnedgång och efter. Exempelvis ser vi att den första personens energibehov minskade med 335 kalorier. (Kuriosa: Personerna gick ner 12,5 procent av sin vikt. Alla dessa personer åt en lågfettkost. I den egentliga studien ingick 21 personer i lågfettsgruppen.)
-335, -800, 37, -977, -447, -698, 177, -223, -84, -623
Hur mycket förändrades kaloribehovet i snitt?
Hur stor är medianen?
- I en undersökning frågar man 750 personer om de anser att det var bättre förr. Resultatet visas i frekvenstabellen nedan (variabeln bättre antar värdet 1 för personer som ansåg att det var bättre förr och värdet 0 för övriga). Hur stort är medelvärdet för variabeln bättre? Förklara också vad medelvärdet betyder i detta fall; beakta då att variabeln är binär.
| bättre | frekvens |
|---|---|
| 0 | 405 |
| 1 | 345 |
- Du kör längs med motorvägen Åbo-Helsingfors och får se fyra skyltar som visar temperaturen. Den första skylten visar 10 grader; den andra 11 grader; den tredje 10 grader och den fjärde 36 grader. För att uppskatta temperaturen längs med motorvägen så skulle då medelvärdet av de olika mätningarna vara ett lämpligt mått. Eller? Förklara varför medianen ger en bättre uppskattning i detta exempel. Hur stor är medianen?
- Ange om följande variabler är kvantitativa eller kvalitativa. Om kvalitativa; ange också om de har data på ordinal- eller nominalnivå.
Kvinna (antar värdet 1 för kvinnor och 0 för män)
Trivsel på jobbet (antar värdena 1, 2, …, 5 där 1 är “usel” och 5 är “utmärkt”)
Lön (mäts i euro per månad)
Blodtyp (A, B, AB och O)
Parti (variabeln visar vilket parti personen röstar på)
Lycka (antar värdena 1, 2, …, 10 där 1 är maximalt olycklig och 10 är maximalt lycklig)
Kursbetyg (Underkänd, 1, 2, …, 5)
Postnummer (t.ex. 20500)
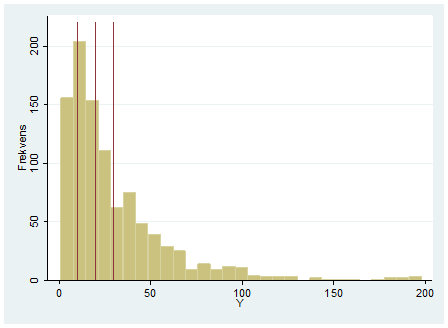
- Se histogrammet nedan. De tre utritade sträcken i rött representerar medelvärdet, medianen och typvärdet (men inte nödvändigtvis i den ordningen). Skriv in rätt lägesmått vid respektive sträck. Ange också om den här fördelningen är skev åt vänster, skev åt höger eller symmetrisk.
- Låddiagrammet nedan visar fördelningen för alkoholkonsumtionen i världens länder. Alkoholkonsumtionen mäts som liter per vuxen invånare.
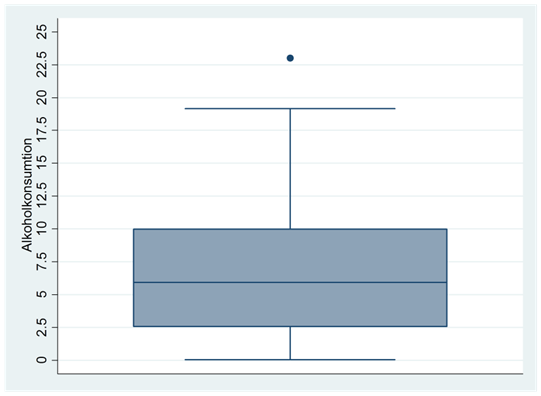
Hur stor är den första kvartilen? Ge också en tolkning av detta värde.
Hur stor är den andra kvartilen? Ge också en tolkning av detta värde.
Hur stor är den tredje kvartilen? Ge också en tolkning av detta värde.
Hur mycket dricks det i det land som har högst alkoholkonsumtion?
- I en tidsanvändningsstudie låter man 300 personer anteckna hur många minuter de använder till att surfa på nätet. I genomsnitt använder personerna 1050 minuter per vecka och den 75:e percentilen är 1680 minuter. Vilket eller vilka av följande påståenden är sanna:
Hälften surfar på nätet mer än 1050 minuter per vecka och hälften mindre.
75 procent av personerna surfar på nätet 1680 minuter per vecka.
25 procent av personerna surfar på nätet mer än 1680 minuter per vecka och 75 procent använder mindre tid än så
Den fjärde kvartilen är 1680 minuter.
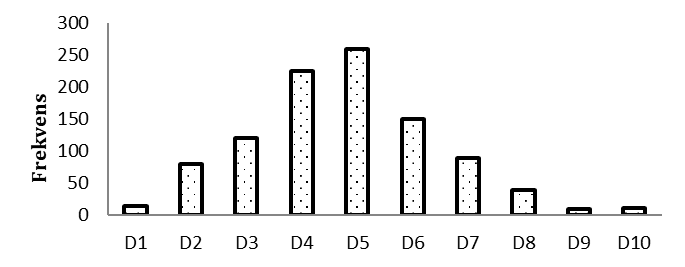
- Vi har samplat 1000 personer och mätt deras inkomster i euro per månad. Vi har delat in personerna i tio decilgrupper, betecknade D1, D2, …, D10. Frekvensdiagrammet nedan visar hur många personer som ingår i respektive decilgrupp. Eller? Förklara vad som inte stämmer med detta frekvensdiagram.
Spridningsmått
-
I uppgift 8 tittade du på förändringen i kaloribehov efter viktnedgång bland 10 personer:
-335, -800, 37, -977, -447, -698, 177, -223, -84, -623
Ett faktum som sticker ut är att det finns en enorm variation från en person till en annan; om du har tur så ökar energibehovet och om du har otur så minskar det med närmare 1000 kalorier. Beräkna variansen och standardavvikelsen för förändringen i kaloribehovet. I snitt minskade energibehovet med 397,3 kalorier.
-
Nedan ser du den procentuella dagliga avkastningen på två aktier, Walmart och Amazon, under de första tio handelsdagarna år 2015. Walmart har i snitt gett en daglig avkastning på 0,72 procent; Amazon har i snitt gett en daglig avkastning på -0,60 procent. Kolumnen “Portfölj” visar din dagliga procentuella avkastning om du investerat hälften av dina pengar i Walmart och hälften i Amazon. Portföljen har i snitt gett en daglig avkastning på 0,07 procent.
Handelsdag Walmart Amazon Portfölj 1 −0,3 −2,1 −1,2 2 0,8 −2,3 −0,7 3 2,7 1,1 1,9 4 2,1 0,7 1,4 5 −1,2 −1,2 −1,2 6 0,7 −1,9 −0,5 7 −0,8 1,1 0,1 8 3,0 −0,5 1,3 9 0,9 −2,2 −0,6 10 −0,7 1,3 0,2
Beräkna volatiliteten för Walmarts aktiekurs. Volatiliteten är standardavvikelsen för aktiens dagliga procentuella avkastning.
Beräkna volatiliteten för Amazons aktiekurs.
Beräkna volatiliteten för portföljen.
Kommentar: Det här exemplet demonstrerar principen om att “inte lägga alla ägg i samma korg”. Notera att portföljens volatilitet är lägre än volatiliteten för Walmart eller Amazon.
- Vilket eller vilka av följande tre påståenden är korrekta?
Variansen kan vara negativ i sampel med negativa värden.
Standardavvikelsen är lika stor i samplet (4, 5, 9, 10) som i samplet (14, 15, 19, 20).
I en löpartävling springer deltagarna 2 kilometer. Löptiden för tävlingsdeltagarna är normalfördelad med medelvärdet 8 minuter och standardavvikelsen 1 minut. Påstående: Ungefär 95 procent av deltagarna har en löptid någonstans mellan 6 och 10 minuter.
- I fråga 17 tittade vi på aktiekursen för Walmart. Vi använde då tio handelsdagar. Histogrammet nedan visar fördelningen för den dagliga avkastningen under de senaste 1167 handelsdagarna. I snitt ligger avkastningen på 0,018 procent med en standardavvikelse på 0,960 procentenheter. Den sista dagen var stängningspriset 63,95 dollar. Utifrån detta kan vi prognostisera att Walmart-aktien kommer att kosta 63,96 dollar dagen därpå (dvs. en ökning med 0,018 procent). Den här prognosen är förstås osäker. Gör nu upp ett prognosintervall för detta pris, dvs. ett intervall som ringar in var priset kommer landa med 95-procentig sannolikhet.
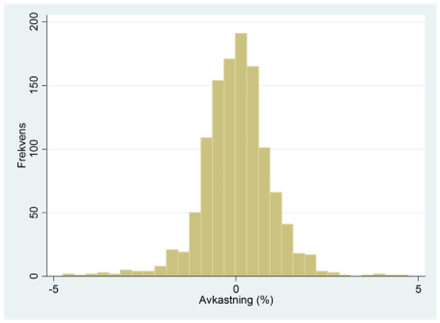
Kommentar: Walmart-aktien visade sig kosta 63,10 dollar nästa dag (som var den 25 augusti 2015).