| Lägenhet | Sovrum | Hyra |
|---|---|---|
| 1 | 1 | 1 800 |
| 2 | 3 | 4 600 |
| 3 | 2 | 2 900 |
| 4 | 1 | 2 100 |
| 5 | 4 | 3 500 |
| … | … | … |
| 44 | 2 | 3 600 |
4 Sambandet mellan två variabler - regressionslinjen
Spridningsdiagrammen nedan representerar samma korrelationskoefficient, r = 0,8.
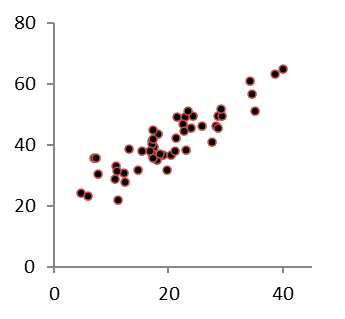
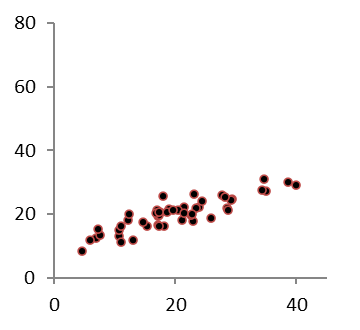
Det finns dock två tydliga skillnader mellan diagrammen som korrelationskoefficienten inte lyckas beskriva:
Datamolnet i det vänstra diagrammet lutar brantare än datamolnet i det högra.
Datamolnet i det vänstra diagrammet ligger på en högre nivå än datamolnet i det högra.
För att beskriva dessa två egenskaper hos ett samband – nivå och lutning – använder vi regressionslinjen.
7. Regressionslinjen, del 1
8. Regressionslinjen, del 2
4.1 Regressionslinjen: Nivå och lutning
Regressionslinjen är en linje som är anpassad för att beskriva data så bra som möjligt:
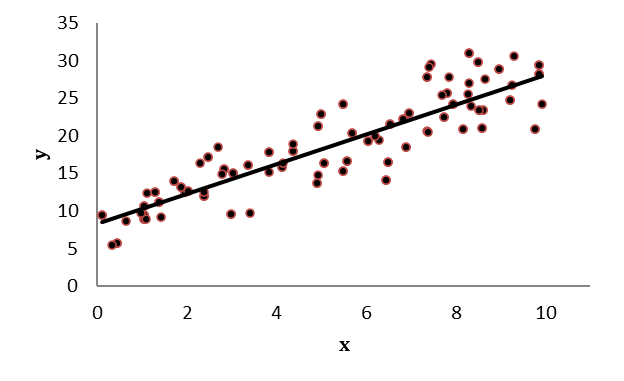
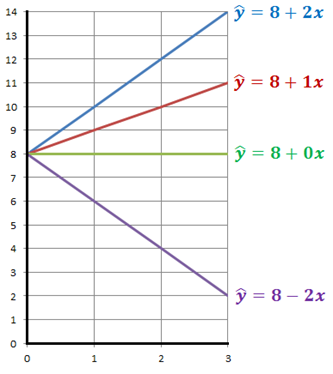
Vi kan beskriva den här linjen genom funktionen för en rät linje: y = a + bx. I figuren ovan ges regressionslinjen av:
\[\widehat{y} = 8 + 2x\]
Vi använder här en “hatt” (^) ovanför y:et. På så vis gör vi en distinktion mellan regressionslinjen (\(\widehat{y}\)) och de faktiska värdena på y-variabeln (y). Om vi istället skrev \(y = 8 + 2x\) så skulle detta inte stämma för varje observation i data, utan enbart för de observationer som råkar ligga exakt på linjen.
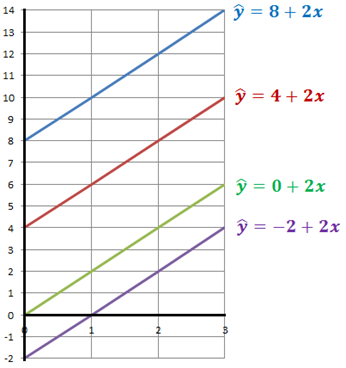
Värdet 8 i den här ekvationen kallas för interceptet och visar var linjen skär y-axeln. Genom att variera interceptet flyttar vi linjen upp och ner i diagrammet:
Värdet 2 i den här ekvationen (\(\widehat{y} = 8 + 2x\)) kallas för koefficienten för x. Den visar hur mycket \(\widehat{y}\) förändras då x ökar med en enhet. Här har koefficienten för x värdet 2: Då x ökar med en enhet så ökar \(\widehat{y}\) med 2 enheter. Genom att variera koefficienten för x så ändrar vi linjens lutning:
Beroende och oberoende variabel
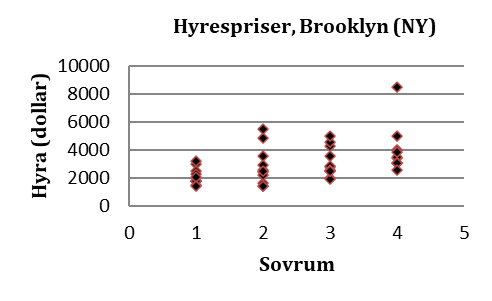
Exempel. Vi vill analysera sambandet mellan antalet sovrum och hyrespriser i Brooklyn, New York. Totalt täcker data 44 lägenheter:
Vi kallar y-variabeln (hyra) för beroende variabel eller utfallsvariabel; x-variabeln (sovrum) kallas för oberoende variabel. Terminologin kommer från att hyran beror av antalet sovrum. När vi gör en regression tänker vi oss att en variabel (x) kan påverka eller prediktera en annan (y). I det här exemplet är det antalet sovrum som predikterar hyrespriset. Därför är hyrespriset beroende variabeln och antalet sovrum oberoende. I ett spridningsdiagram läggs den beroende variabeln (y) alltid på y-axeln.
Här är ytterligare två exempel: Vi studerar sambandet mellan rökning under graviditeten och barnets födelsevikt. Rökning är då oberoende variabel (x) och barnets födelsevikt beroende (y). Vi studerar sambandet mellan arbetserfarenhet och lön. Arbetserfarenhet är då oberoende variabel och lön beroende.
Att beräkna regressionslinjens ekvation
Exempel fortsättning. Spridningsdiagrammet nedan visar sambandet mellan antalet sovrum och hyrespriser i Brooklyn:
För att få fram regressionslinjen ska vi beräkna värdena för a och b i ekvationen:
\[\widehat{hyra} = a + b \times sovrum\]
Vi får b som kovariansen genom variansen för x:
\[\ \ \ \ \ b = \frac{s_{xy}}{s_{x}^{2}} = \frac{kovariansen\ mellan\ x\ och\ y}{variansen\ för\ x}\ \ \ \ \ \]
När vi vet b så gäller det ännu att sätta nivån på linjen som:
\[\ \ \ \ \ a = \overline{y} - b\overline{x}\ \ \ \ \ \]
När man använder de här formlerna för att beräkna regressionslinjen så säger man att man använder metoden OLS (från engelskans ordinary least squares; svenska: minsta-kvadratmetoden.).1 OLS ger oss en linje som uppskattar hur medelvärdet för y varierar med olika värden på x – hur genomsnittlig hyra varierar med antalet sovrum. Regressionslinjen kan som regel inte gå exakt genom medelvärdena, men regressionslinjen är den bästa linjära approximationen för hur genomsnittlig hyra varierar med antalet sovrum. I kapitlets Appendix (A.1: OLS eller minsta-kvadratmetoden) kan du läsa mer om bakgrunden till regressionslinjen.
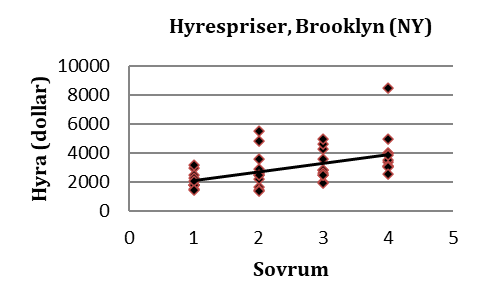
I detta exempel är kovariansen mellan variablerna 767,87; variansen för antalet sovrum är 1,28.
\[ \mathbf{b} = \frac{{\text{kovariansen}}}{{\text{variansen för } x}} = \frac{\color{blue}{767,87}}{\color{red}{1,28}} \approx 600 \]
Genomsnittlig hyra (\(\overline{y}\)) är 3025,93 och genomsnittligt antal sovrum (\(\overline{x}\)) är 2,5:
\[ \mathbf{a} = \overline{y} - b\overline{x} = {\color{blue}{3025,93}} - {\color{black}{600,37}} \times {\color{red}{2,5}} \approx 1525 \]
Regressionslinjen ges då av: \(\widehat{hyra} = 1525 + 600\times{sovrum}\)
Regressionslinjens tolkning
Exempel fortsättning. Vi hade regressionslinjen:
\[\widehat{hyra} = 1525 + 600\times{sovrum}\]
Så vad säger den?
\(\widehat{hyra}\) är den predikterade hyran. Den predikterade hyran är en uppskattning av den genomsnittliga hyran. \(\widehat{hyra}\) är också vår bästa gissning: Om vi vet att en lägenhet har, säg, två sovrum uppskattas hyran vara 2725 dollar:
\[ \widehat{hyra} = 1525 + 600 \times \underbrace{sovrum}_{=2} = 2725 \]
2725 dollar är alltså en uppskattning av hur mycket det i snitt kostar att hyra en lägenhet i Brooklyn med två sovrum. Vi kan också få en sådan uppskattning genom att direkt beräkna det genomsnittliga hyrespriset bland alla lägenheter i data med två sovrum. Men regressionslinjen är en förbättring på den uppskattningen eftersom vi nu tar hjälp av hela vårt datamaterial. Detta bygger dock på att förhållandet mellan hyrespriset och antalet sovrum också är linjärt.
På motsvarande sätt kan vi räkna ut att den predikterade hyran för en lägenhet med tre rum är 3325 dollar:
\[\widehat{hyra} = 1525 + 600 \times \underbrace{sovrum}_{=3} = 3325\]
Och att den predikterade hyran för en lägenhet med fyra sovrum är 3925 dollar:
\[\widehat{hyra} = 1525 + 600 \times \underbrace{sovrum}_{=4} = 3925\]
Vi kan till och med prediktera hyran för en lägenhet med fem sovrum trots att vi inte har en enda sådan lägenhet i data:
\[\widehat{hyra} = 1525 + 600 \times \underbrace{sovrum}_{=5} = 4525\]
När vi på detta vis gör prediktioner “utanför samplet” så kallas det för att extrapolera.
Exempel fortsättning. Vi hade regressionslinjen:
\[\widehat{hyra} = 1525 + 600\times{sovrum}\]
Hur tolkas regressionskoefficienten (som här har värdet 600)? Jo, denna säger att hyran predikteras öka med 600 dollar för varje ytterligare sovrum. Eller med lite andra ord: För varje ytterligare sovrum så stiger hyran i snitt med 600 dollar.
Vi kan se att detta stämmer genom att testa oss fram, dvs. mäta hur mycket hyran predikteras öka då antalet sovrum ökar med ett. Nedan har vi predikterat hyran för en lägenhet med k stycken sovrum (där k kan vara vad som helst). Sen jämför vi detta med en lägenhet med ett sovrum mer, dvs. k+1 stycken sovrum.
Predikterad hyra för en lägenhet med k antal rum:
\[\color{blue}{\widehat{hyra} = 1525 + 600 \times k}\]
Predikterad hyra för en lägenhet med k+1 antal rum:
\[\color{red}{\widehat{hyra} = 1525 + 600 \times (k + 1)}\]
Skillnaden: \({\color{red}{1525 + 600 \times (k + 1)\rbrack}} - {\color{blue}{(1525 + 600 \times k)}} = 600\)
Exempel fortsättning. Vi hade regressionslinjen:
\[\widehat{hyra} = 1525 + 600\times{sovrum}\]
Hur tolkas interceptet (som här har värdet 1525)? Interceptet visar var linjen skär y-axeln. Ofta har interceptet ingen annan naturligare tolkning. Vi skulle kunna säga att interceptet är den predikterade hyran för en lägenhet med noll stycken sovrum:
\[\widehat{hyra} = 1525 + 600 \times \underbrace{sovrum}_{=0} = 1525\]
Men eftersom det inte är meningsfullt att tala om en lägenhet med noll sovrum så är det kanske här bättre att tänka på interceptet som den siffra som “sätter nivån”.
Exempel fortsättning. Visa att regressionslinjen går genom medelvärdena för x och y.
Om vi stuvar om i uttrycket för interceptet så får vi:
\[\ \ \ \ \ \overline{y} = a + b\overline{x}\ \ \ \ \ \]
Eller med andra ord: Om vi predikterar hyran för en lägenhet med ett genomsnittligt antal rum så får vi ut den genomsnittliga hyran.
Procent och procentenheter
Det är inte ovanligt att vi jobbar med variabler som mäts i procent (t.ex. arbetslöshet eller andelen kvinnor i styrelsen). I dessa fall är det viktigt att vara noggrann med enheten. Vi ser bäst varför genom ett exempel.
Exempel. Spridningsdiagrammet nedan visar sambandet mellan sysselsättningsgrad och självmordsfrekvens bland män i 169 länder. Variabeln sysselsättning mäter hur stor procent av männen i landet som är sysselsatta; variabeln självmord mäter antalet självmord per hundratusen män.
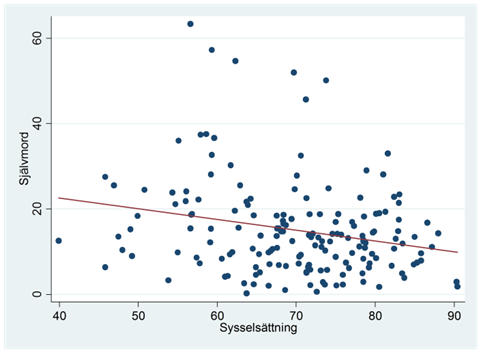
Regressionslinjen ges av:
\[\widehat{självmord} = 32,6 - 0,25\ sysselsättning\]
Hur tolkar vi regressionskoefficienten (-0,25)? Jo, då sysselsättningsgraden ökar med en procentenhet så minskar antalet självmord i snitt med 0,25 per hundratusen män. Notera här att vi talar om procentenheter och inte procent! Varför? Jo, det vi egentligen vill säga är att när sysselsättningen ökar med ett – till exempel från 60 till 61 procent eller från 85 till 86 procent – så minskar antalet självmord i snitt med 0,25 per hundratusen män. Men en ökning från 60 till 61 procent än inte en enprocentig ökning, utan en ökning med 1,7 procent (61/60 ≈ 1,017). Däremot är det en ökning med en procentenhet.
Med andra ord: Om din x- eller y-variabel mäts i procent så uttrycks skillnader (t.ex. från 5% till 6%) i procentenheter. Om du talar om procent istället så blir tolkningen av resultatet galen.
Residualer
Exempel. Vi ska återgå till exemplet med hyrespriser i Brooklyn. Vi såg tidigare hur vi kan prediktera hyran för lägenheter med olika antal sovrum. I tabellen nedan har vi predikterat hyran för varje lägenhet i data:
| Lägenhet | Sovrum | Hyra | Predikterad hyra |
|---|---|---|---|
| 1 | 1 | 1 800 | 2 125 |
| 2 | 3 | 4 600 | 3 325 |
| 3 | 2 | 2 900 | 2 725 |
| 4 | 1 | 2 100 | 3 325 |
| 5 | 4 | 3 500 | 3 925 |
| … | … | … | … |
| 44 | 2 | 3 600 | 2 725 |
Exempelvis ser vi att lägenhet #2 har en hyra på 4600 dollar men en predikterad hyra på 3325 dollar. Den här lägenheten kostar alltså 1275 dollar mer än predikterat utifrån antalet sovrum. Vi kallar den här skillnaden för residualen. Residualen visar “felet”; hur mycket lägenhetens faktiska hyra avviker från den predikterade. Residualen för lägenhet #1 är -325 dollar; lägenheten kostar 325 dollar mindre än predikterat. I tabellen nedan visas residualen för varje lägenhet i data:
| Lägenhet | Sovrum | Hyra | Predikterad hyra | Residual |
|---|---|---|---|---|
| 1 | 1,0 | 1 800 | 2 125 | −325 |
| 2 | 3,0 | 4 600 | 3 325 | 1 275 |
| 3 | 2,0 | 2 900 | 2 725 | 175 |
| 4 | 1,0 | 2 100 | 3 325 | −1 225 |
| 5 | 4,0 | 3 500 | 3 925 | −425 |
| … | … | … | … | … |
| 44 | 2,0 | 3 600 | 2 725 | 875 |
| Medelvärde: | 2,5 | 3 026 | 3 026 | 0 |
Om vi summerar ihop alla residualer så kommer vi att se att summan landar på noll; regressionslinjen överskattar hyran för vissa lägenheter och underskattar den för andra, men i genomsnitt har regressionslinjen rätt. På motsvarande sätt så är snittet för de predikterade hyrorna lika med snittet för de faktiska. Det är ett annat sätt att säga samma sak; regressionslinjen har rätt i genomsnitt. Det här innebär inte att regressionslinjen inte kan göra brutalt felaktiga prediktioner ibland. Detta kan hända eftersom vi lever i en komplex värld som inte låter sig predikteras så lätt. Detta kan också hända om förhållandet mellan y och x inte är linjärt trots att vi beskriver det så. Vi ska återkomma till den punkten i avsnitt 4.4.
4.2 Förklaringsgraden
Om vi kör en regression i ett program som kan hantera statistiska data så får vi fram ett resultat som ser ut ungefär såhär:
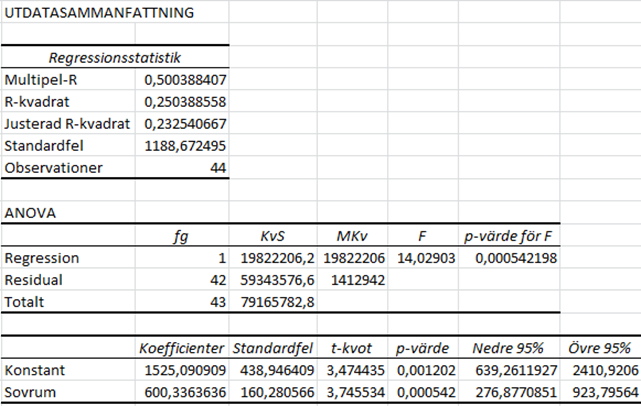
Den här regressionen är gjord i Excel, men regressionsutskriften är uppbyggd på liknande sätt oavsett vilket dataprogram du använder. Data är Brooklyn hyresdata som vi är bekanta med från tidigare. Som du ser innehåller utskriften många siffror. Alla är dock inte lika intressanta och i det här skedet ska vi bara koncentrera oss på några av dem. För det första: Var syns regressionslinjen i den här utskriften? Eller med andra ord: Var syns värdena för a och b i uttrycket \(\widehat{hyra} = a + b \times sovrum\)? Jo, vi hittar dem i den tredje tabellen, i kolumnen “Koefficienter”:
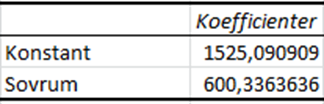
Det som kallas för “Konstant” i tabellen är interceptet (a) som har värdet 1525,09… ; koefficienten för antal sovrum (b) har värdet 600,33… .
Vi ska också titta lite mer på en annan siffra ur regressionsutskriften, nämligen förklaringsgraden som betecknas R2:
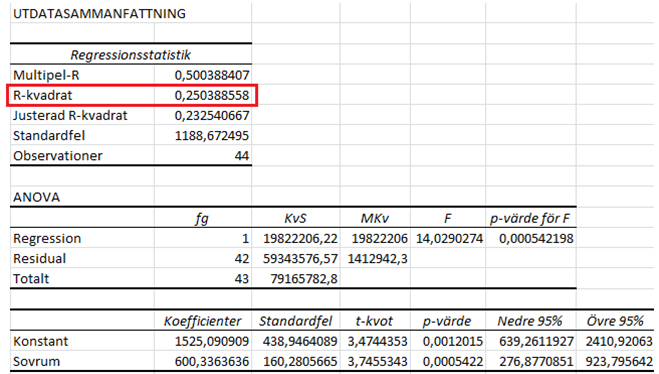
Förklaringsgraden anger andelen av variation i y som kan förklaras av x. Vi har R2 = 0,25: 25 procent av variationen i hyrespriser kan förklaras av antalet sovrum.
Förklaringsgraden är alltså en andel och kan därför anta värden mellan 0 och 1. Då förklaringsgraden har värdet 0 så kan variationen i y inte alls förklaras av x. Eller med andra ord: x hjälper oss inte alls att prediktera y. Då förklaringsgraden har värdet 1 så betyder det att all variation i y kan förklaras av x. Eller med andra ord: Då vi använder regressionslinjen, \(\widehat{hyra} = 1525 + 600 \times sovrum\), för att prediktera hyran för en lägenhet så får vi alltid ut lägenhetens faktiska hyra. Det här skulle betyda att residualen är exakt lika med noll för varje lägenhet i data. (Kom ihåg att residualen är skillnaden mellan lägenhetens faktiska hyra och den predikterade.)
Förklaringsgraden kan beräknas som kvadraten på Pearsons korrelationskoefficient. Men för att se vad som händer bakom beräkningarna så kan följande formel vara till större nytta:
\[\ \ \ \ R^{2} = 1 - \frac{variansen\ i\ residualerna}{variansen\ i\ y}\ \ \ \ \ \]
Om variansen i residualerna är stor så innebär det att de faktiska hyrespriserna ofta är mycket större eller mycket mindre än predikterat. I extremfallet är variansen i residualerna lika stor som variansen i faktiska hyrespriser. Då blir kvoten i uttrycket ovan 1 och R2 blir 0.
Om variansen i residualerna är liten så betyder det att de faktiska hyrespriserna ligger nära det som predikterats utifrån antalet rum. I extremfallet är variansen i residualerna 0 (alla residualer har värdet 0) och R2 blir då 1.
4.3 Logaritmerad skala
Exempel. Nedan ges sambandet mellan antalet skolår och lön för 1000 personer (fejkat data).
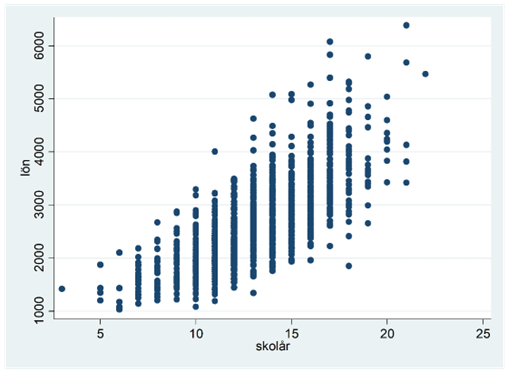
Från spridningsdiagrammet kan man ana sig till att sambandet kunde beskrivas bättre av en linje om vi loggade y-variabeln: tänk dig att du pressar ihop y-axeln så att stora värden straffas extra hårt – detta kunde göra ett tydligare linjärt mönster i data. Här visas sambandet då lönen beskrivs på en logaritmisk skala:
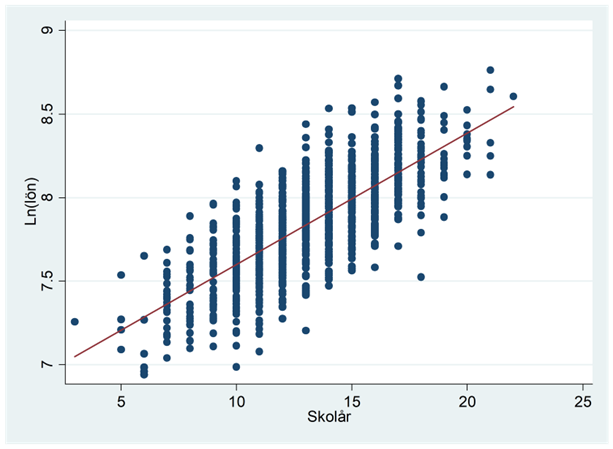
Vi räknar ut regressionslinjen på samma sätt som tidigare, bara att den beroende variabeln nu är ln(lön) istället för lön. Ett utdrag av data ges nedan:
| Id | Skolår | Lön | ln(lön) |
|---|---|---|---|
| 1 | 18 | 2 967 | 7,995 |
| 2 | 12 | 3 480 | 8,155 |
| 3 | 11 | 4 009 | 8,296 |
| 4 | 11 | 1 933 | 7,567 |
| 5 | 13 | 2 599 | 7,863 |
| 6 | 10 | 2 339 | 7,757 |
| … | … | … | … |
| 1000 | 8 | 1 459 | 7,286 |
Regressionslinjen ges av:
\[\widehat{ln(lön)} = 6,8 + {\color{red}{0,08}} \times {skolår}\]
Då antalet skolår ökar med ett så ökar den naturliga logaritmen av lönen i snitt med 0,08 enheter. Eller med andra ord: Då antalet skolår ökar med ett så ökar lönen i snitt med 8 procent.
Som du märker så får vi en procentuell effekt då utfallet är loggat. Hur kommer det sig? Jo, tidigare (avsnitt 2.2) såg vi att skillnaden mellan två loggade värden representerar den procentuella skillnaden mellan värdena. Exempel: Om ln(lön) ökar med 0,08 enheter så representerar detta en åttaprocentig ökning i lönen.
Exempel. I avsnitt 3.2 tittade vi på förhållandet mellan inkomst och livslängd i världens länder:
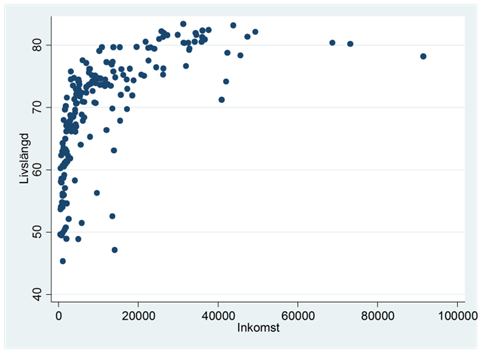
där inkomst mäter inkomst per person i landet; livslängd mäter genomsnittlig livslängd i landet. Vi såg också att vi här kan logga inkomsterna för att få ett linjärt samband:
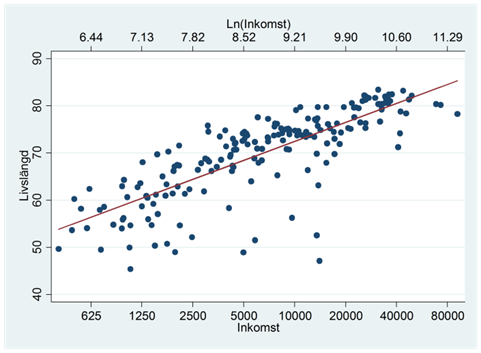
Här ges regressionslinjen av:
\[\widehat{livslängd} = 19,0 + {\color{red}{5,8}} \times ln(inkomst)\]
Då den naturliga logaritmen av inkomst ökar med en enhet så ökar livslängden i snitt med 5,8 år. Och på samma sätt: Då den naturliga logaritmen av inkomst ökar med 0,01 enheter så ökar livslängden i snitt med 0,058 år. Eller med andra ord: Då inkomsterna ökar med en procent så ökar livslängden i snitt med 0,058 år.
Som du ser så beskriver vi nu inkomstökningar i procent (och inte i absoluta tal). Om de logaritmerade inkomsterna ökar med 0,01 enheter så motsvarar ju detta en ökning i inkomsterna med 1 procent och en ökning i livslängden med, i snitt, 0,058 år.
I tabellen nedan visas hur koefficienterna tolkas i olika fall, dvs. beroende på om y är loggad, om x är loggad, eller om bägge är loggade:
| Regression | Tolkning |
|---|---|
| \[\widehat{ln(y)} = 2 + {\color{red}{0,1}} \times x\] | Då x ökar med en enhet så ökar y med \({\color{red}{0,1}}\times 100\) = 10 procent. |
| \[\widehat{ln(y)} = 2 + {\color{red}{0,1}} \times ln(x)\] | Då x ökar med en procent så ökar y med \(\color{red}{0,1}\) procent. |
| \[\widehat{y} = 2 + {\color{red}{0,1}} \times ln(x)\] | Då x ökar med en procent så ökar y med \({\color{red}{0,1}}/100\) = 0,001 enheter. |
De här tolkningarna gäller dock enbart ungefärligt, och då de procentuella effekterna blir allt större så blir dessa approximationer allt sämre. Om effekten på y är större än plus/minus 10 procent så kan man istället använda exakta omvandlingsformler. I regressioner med loggat utfall och ologgad x-variabel så är detta inte ovanligt. Anta exempelvis att vi får följande resultat:
\[\widehat{ln(y)} = 2 + 0,2 \times x\]
Den exakta omvandlingen: Om x ökar med en enhet så ökar y med \(\left( e^{0,2} - 1 \right) \times 100 \approx 22\) procent.
Exempel. Regressionen nedan bygger på data för olika länder. Här har vi tittat på sambandet mellan åldern då kvinnor gifter sig och antalet barn per kvinna:
\[\widehat{\ln(antal\ barn)} = 2,97 - 0,082 \times ålder\]
Då åldern när kvinnor gifter sig ökar med ett, så minskar antalet barn per kvinna i snitt med 8 procent.
Hur stor är den procentuella effekten på antalet barn, om giftermålsåldern ökar med 10 år? Jo, då predikteras antalet barn per kvinna minska med 56 procent:
\[\left( e^{- 0,082 \times 10} - 1 \right) \times 100 \approx - 56\]
I kapitlets Appendix (A.2 Log-procenter) visas de exakta omvandlingsformlerna för alla tre fall, dvs. beroende på om y loggats, x loggats eller bägge.
4.4 Dummy-variabler
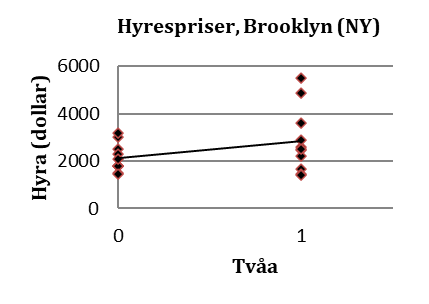
Exempel. Vi ska fortsätta med exemplet gällande hyrespriser i Brooklyn. Anta nu att vi enbart valt ut en- och tvårummare till vår analys. Det finns inget som hindrar oss från att göra en regressionslinje trots att x-variabeln enbart har två värden. Så här ser data då ut:
| Lägenhet | Sovrum | Hyra |
|---|---|---|
| 1 | 1 | 1 800 |
| 2 | 2 | 1 450 |
| 3 | 2 | 2 900 |
| 4 | 1 | 2 100 |
| 5 | 1 | 2 300 |
| … | … | … |
| 22 | 2 | 3 600 |
Variabeln sovrum kallas nu för en dummy-variabel; det är en x-variabel som enbart antar två olika värden. Dummy-variabler brukar dock kodas med värdena 0 och 1 (det underlättar tolkningen av resultaten). Så låt oss döpa om variabeln sovrum till tvåa; variabeln tvåa antar värdet 1 om lägenheten har två sovrum och värdet 0 om lägenheten har ett sovrum:
| Lägenhet | Tvåa | Hyra |
|---|---|---|
| 1 | 0 | 1 800 |
| 2 | 1 | 1 450 |
| 3 | 1 | 2 900 |
| 4 | 0 | 2 100 |
| 5 | 0 | 2 300 |
| … | … | … |
| 22 | 1 | 3 600 |
Regressionslinjen ges av: \(\widehat{hyra} = 2115 + 713 \times tvåa\). Den predikterade hyran för en tvåa är då 2828 dollar:
\[\widehat{hyra} = 2115 + 713 \times \underbrace{tvåa}_{=1} = 2115 + 713 = 2828\]
Och att den predikterade hyran för en etta är 2115 dollar:
\[\widehat{hyra} = 2115 + 713 \times \underbrace{tvåa}_{=0} = 2115\]
I det här fallet är prediktionen för en tvårummare (2828 dollar) den genomsnittliga hyran bland tvårummarna i data. Prediktionen för en etta (2115 dollar) är den genomsnittliga hyran bland enrummarna i data. Regressionslinjen går med andra ord exakt genom snittet för en- och tvårummare. Regressionskoefficienten (på 713 dollar) är den genomsnittliga skillnaden i hyra mellan två- och enrummare.
Exempel. Vi har frågat 20 stycken sista årets läkarstuderande om deras lönekrav på första jobbet, dvs. vilken är den lägsta lön de kunde tänka sig att acceptera? Tabellen nedan visar lönekraven och personernas kön (variabeln kvinna antar värdet 1 för kvinnor och 0 för män):
| Id | Kvinna | Lönekrav |
|---|---|---|
| 1 | 0 | 3 500 |
| 2 | 0 | 2 900 |
| 3 | 0 | 3 200 |
| 4 | 0 | 3 000 |
| 5 | 0 | 3 600 |
| 6 | 0 | 3 400 |
| 7 | 0 | 3 000 |
| 8 | 0 | 3 500 |
| 9 | 0 | 4 000 |
| 10 | 0 | 2 900 |
| 11 | 1 | 3 500 |
| 12 | 1 | 3 000 |
| 13 | 1 | 3 100 |
| 14 | 1 | 2 500 |
| 15 | 1 | 3 200 |
| 16 | 1 | 2 850 |
| 17 | 1 | 3 200 |
| 18 | 1 | 3 700 |
| 19 | 1 | 2 900 |
| 20 | 1 | 3 050 |
Genomsnittligt lönekrav bland männen är 3300 euro och bland kvinnorna 3100 euro. Regressionslinjen ges då av:
\[\widehat{lönekrav} = 3300 - 200 \times kvinna\]
Koefficienten för kvinna visar att lönekravet i snitt är 200 euro lägre bland kvinnorna än bland männen.
Det kan verka onödigt krångligt att beskriva det som bara är skillnaden mellan två medelvärden med hjälp av en regressionsekvation. Varför skulle vi i exemplet ovan använda en regressionsekvation då det är både lättare och intuitivare att säga att männen snittar 3300 euro och kvinnorna 3100? Det finns faktiskt ingen poäng, åtminstone inte än så länge. Men i kommande kapitel kommer vi att märka nyttan av att kunna använda dummy-variabler i ekvationer!
Sammanfattning
Appendix
A.1 OLS eller minsta-kvadratmetoden
Inom statistiken gör vi ofta prediktioner eller uppskattningar (Hur mycket predikteras det kosta att hyra en lägenhet i Brooklyn med två sovrum?). Till vår hjälp tar vi naturligtvis data. Men hur gör vi en bästa prediktion utifrån data? Vad som är “bäst” är delvis en subjektiv fråga. Vi vill naturligtvis pricka så nära som möjligt och ju större fel desto sämre.

Men hur ska vi värdera ett fel på 0,5 enheter mot ett fel på, säg, 10 eller 100 enheter? När vi gör en regression med OLS har vi en kvadratisk förlustfunktion – vi väljer den regressionslinje som minimerar summan av de kvadrerade felen (residualerna). Låt oss ta ett exempel på vad detta kan betyda i ett lite annat sammanhang: I Kalles klass går tre elever. Eleverna bor 1, 2 och 6 kilometer från skolan. Hur lång väg har Kalle till skolan? Utan någon annan information så måste du gissa. Anta att du har en kvadratisk förlustfunktion; om du gissar “1 km” och om sanningen är “6 km” så blir felet 5 och förlusten 25. Så vad ska du gissa för att minimera den förväntade förlusten? Jo, 3 km, dvs. medelvärdet. Det här är ingen tillfällighet – med en kvadratisk förlustfunktion så är medelvärdet alltid vår bästa gissning. Om du är bekant med derivering kan du se detta på följande sätt: Uttrycket nedan beskriver förlusten som en funktion av din gissning (\(\widehat{y}\)). Hur stor förlusten blir beror ju förstås på vad som är sant (1, 2 eller 6 km) men vi kan helt enkelt summera ihop de tre möjligheterna:
\[{\sum_{}^{}{Förlust} = (1 - \widehat{y})}^{2} + {(2 - \widehat{y})}^{2} + {(6 - \widehat{y})}^{2} = 41 - 18\widehat{y} + 3{\widehat{y}}^{2}\]
För att hitta den prediktion (\(\widehat{y}\)) som minimerar förlusten så deriverar vi denna med avseende på \(\widehat{y}\), sätter lika med 0 och löser ut \(\widehat{y}\). Detta ger \(\widehat{y}\ = 3\). (Och andra derivatan är positiv så detta är den gissning som ger den lägsta förlusten.) Då vi kör en regression så har vi samma situation bara att \(\widehat{y} = a + bx\). Detta ger oss de formler som vi såg tidigare i kapitlet. Regressionslinjen kan alltså betraktas som ett slags medelvärde – ett betingat medelvärde.
A.2 Log-procenter
Nedan ges exakta omvandlingformer då x, y (eller båda) är logaritmerade.
| Regression | Tolkning |
|---|---|
| \[\widehat{ln(y)} = 2 + {\color{red}{0,1}} \times x\] | Då x ökar med en enhet så ökar y med \(\left( e^{{\color{red}{0,1}}} - 1 \right) \times 100 \approx 10,5\) procent. |
| \[\widehat{ln(y)} = 2 + {\color{red}{0,1}} \times ln(x)\] | Då x ökar med en procent så ökar y med \(\left( {1,01}^{{\color{red}{0,1}}} - 1 \right) \times 100 \approx 0,10\) procent. |
| \[\widehat{y} = 2 + {\color{red}{0,1}} \times ln(x)\] | Då x ökar med en procent så ökar y med \({\color{red}{0,1}}\times{ln(1,01)}\approx 0,001\) enheter. |
Exempel. Ta regressionen:
\[\widehat{ln(y)} = 2 + {\color{red}{0,1}} \times ln(x)\]
Tolkning: Då x ökar med en procent så ökar y i snitt med 0,1 procent. Hur stor blir effekten på y om x ökar med 10 procent? Låt oss använda den exakta omvandlingsformeln:
Då x ökar med 10 procent så ökar y med \(\left( {1,1}^{\color{red}{0,1}} - 1 \right) \times 100 \approx 0,96\) procent.
Hur stor blir effekten på y om x ökar med 100 procent? Den exakta omvandlingsformeln visar att svaret är 7,18 procent:
Då x ökar med 10 procent så ökar y med \(\left( 2^{\color{red}{0,1}} - 1 \right) \times 100 \approx 7,18\) procent.
Exempel. Ta regressionen:
\[\widehat{y} = 2 + {\color{red}{0,1}} \times ln(x)\]
Tolkning: Då x ökar med en procent så ökar y i snitt med 0,001 enheter. Hur stor blir effekten på y om x ökar med 10 procent? Låt oss testa den exakta omvandlingsformeln:
Då x ökar med 10 procent så ökar y med \({\color{red}{0,1}}\times ln(1,1) \approx 0,0095\) enheter.
Och på motsvarande sätt:
Då x ökar med 100 procent så ökar y med \({\color{red}{0,1}}\times ln(2) \approx 0,069\) enheter.
De här exemplen visar att de exakta omvandlingformlerna kan bli relevanta då vi vill ändra enhet; titta på effekten av en 10- eller 100-procentig ökning (istället för en 1-procentig).
Övningsuppgifter
Regressionslinjen: Nivå och lutning
- En av regressionslinjerna nedan beskrivs av ekvationen \(\widehat{y} = 20 + 2x\); en annan av ekvationen \(\widehat{y} = 80 - x\); en tredje av ekvationen \(\widehat{y} = - 20 + 3x\) och en fjärde av ekvationen \(\widehat{y} = 20 + 0x\). Para ihop rätt regressionslinje med rätt diagram (A, B, C och D).
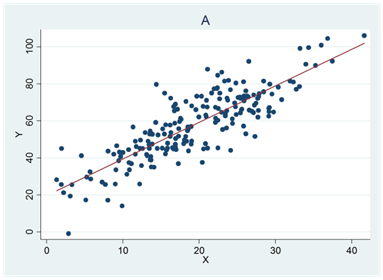
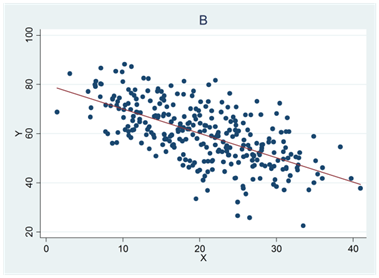
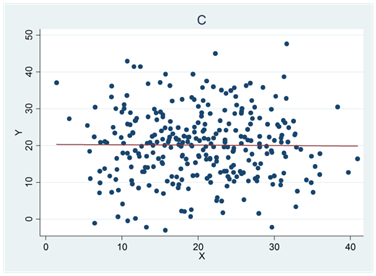
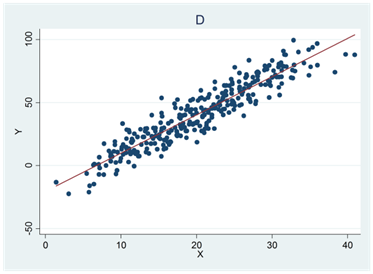
- Nedan beskrivs fyra olika samband. Vilken variabel är beroende och vilken är oberoende i respektive fall?
Är erfarna lärare bättre? Vi samplar slumpmässigt ett hundratal skolklasser i årskurs nio. Vi mäter mattelärarens erfarenhet i antal år (variabeln erfarenhet) och skolklassens genomsnittliga resultat på ett nationellt matteprov (variabeln matteprov).
Har långa basketspelare högre lön är korta? För att besvara denna fråga samlar vi in data för ett hundratal professionella basketspelare, deras längd (variabeln längd) och lön (variabeln lön).
Ledde Tjernobylkatastrofen år 1986 till fler cancerpatienter? Vi samlar in data över radioaktivt nedfall (variabeln nedfall) för ~50 städer i Ukraina år 1986, där vissa städer drabbades hårdare än andra. För varje stad mäter vi andelen cancerpatienter (variabeln cancer) bland ungdomar som var i fosterstadiet år 1986.
Du samlar in ett datamaterial för ett hundratal barn i syfte att mäta sambandet mellan barnets längd (variabeln längd) och föräldrarnas genomsnittliga längd (variabeln förlängd).
- Arbetslösheten i Europa har länge legat på en högre nivå än den i USA. Många skyller detta på en tungrodd offentlig sektor och högt skattetryck. Kan det ligga någonting i detta? Spridningsdiagrammet nedan visar sambandet mellan skatteprocent och arbetslöshet i olika länder. Variabeln skatteprocent mäter skatteintäkterna som en procent av hela ekonomin; arbetslöheten mäter arbetslöshetsgraden i procent. Kovariansen mellan variablerna är 8,9061; genomsnittlig arbetslöshet är 8,4733 procent och den genomsnittliga skatteprocenten är 16,4505; standardavvikelsen för skatteprocenten är 6,1648 och standardavvikelsen för arbetslöshetsgraden är 5,5243.
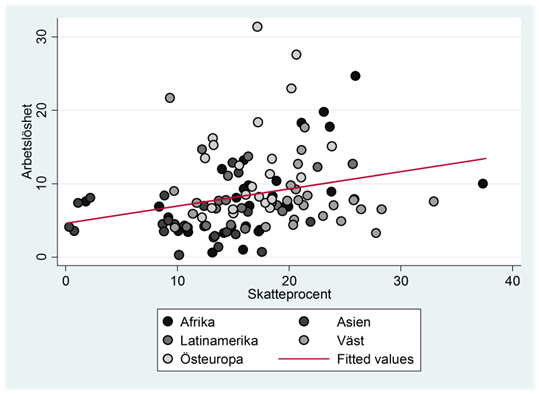
Beskriv regressionslinjen med en regressionsekvation. Ge också en tolkning av koefficienten b i den här regressionen.
Se fråga a: I Finland ligger skatten på 19,83 procent. Hur stor predikteras arbetslösheten vara i Finland?
- Är resultaten sämre i stora skolklasser än i små? För att ta reda på detta har vi samplat 80 skolklasser och mätt antalet elever på klassen (variabeln elevantal) och klassens genomsnittliga betyg (variabeln betyg). Du vill nu mäta sambandet med hjälp av en regressionslinje: \(\widehat{betyg} = a + b \times elevantal\). Korrelationen mellan variablerna är -0,25; i snitt går det 20 elever i en klass och genomsnittligt betyg är 7,5; standardavvikelsen för antalet elever i klassen är 2,5 och standardavvikelsen för betyget är 0,3.
Beskriv regressionslinjens ekvation.
Tolka koefficienten för elevantal.
Rita upp regressionslinjen i ett diagram enligt mallen nedan. (Notera att axlarna inte börjar vid origo.) Skriv också ut variablernas namn på y- och x-axeln.
- Hur stiger VD:ns lön med antalet år på posten? För att besvara denna fråga använder vi ett sampel för 177 amerikanska företag år 1990. Regressionen nedan beskriver sambandet mellan erfarenhet (hur många år VD:n suttit på posten) och lön (VD:ns lön i tusentals dollar).
\[\widehat{lön} = 772,43 + 11,75erfarenhet\]
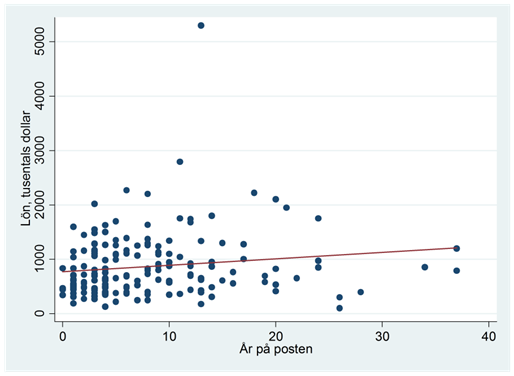
Hur mycket högre predikteras lönen vara för en VD med 20 års erfarenhet i jämförelse med en purfärsk VD (dvs. 0 års erfarenhet)?
Tolka koefficienten för erfarenhet.
Hur mycket ökar lönen i snitt då erfarenheten ökar med tio år? Femton år?
Hur mycket ska arbetserfarenheten öka för att lönen ska stiga med hundratusen dollar?
Som du ser från spridningsdiagrammet ovan så finns det en VD med en extra hög lön (5 299 000 dollar). Den här personen har 13 års erfarenhet. Hur stor är residualen för denna VD?
En annan VD i samplet har två års erfarenhet och en lön på 471 000 dollar. Hur stor är residualen för denna VD?
Förklaringsgraden
- Se uppgift 4: Hur stor är förklaringsgraden? Ge också en tolkning av förklaringsgraden för det aktuella fallet.
- Se uppgift 5: Här blir förklaringsgraden 0,020. Vilket eller vilka av följande påståenden är sanna?
Korrelationen mellan VD:ns lön och antalet år på posten är ~0,14.
2 procent av observationerna ligger på regressionslinjen.
2 procent av variationen i VD-löner kan förklaras av antalet år på posten.
Logaritmerad skala
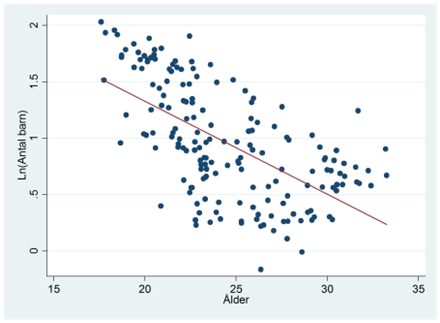
- Det föds allt färre barn. En möjlig orsak är att kvinnor skjuter upp äktenskap och barnafödande och satsar på utbildning och karriär. Spridningsdiagrammet nedan visar sambandet mellan åldern då kvinnor gifter sig och antalet barn per kvinna för 175 länder. Variabeln ålder mäter den genomsnittliga åldern då kvinnor i landet gifter sig; antal barn mäter genomsnittligt antal barn per kvinna. Regressionslinjen ges av: \(\widehat{ln(antal\ barn)} = 2,97 - 0,082 \times ålder\). Tolka koefficienten för ålder.
- Vi har mätt risken för att åka fast samt brottsligheten i 89 amerikanska orter. Brottsligheten mäts som antalet brott per invånare; risken för att åka fast är andelen av alla brott som leder till ett arresterande. Sambandet kan beskrivas genom regressionen:
\[\ln(brottslighet) = - 4,18 - 0,50 \times ln(risk\ att\ åka\ fast)\]
Vilken eller vilka av följande fyra tolkningar är korrekt?
Då risken för att åka fast ökar med en procent så minskar antalet brott per invånare i snitt med 0,5 procent.
Då risken för att åka fast ökar med en procentenhet så minskar antalet brott per invånare i snitt med 0,5 procent.
Då risken för att åka fast ökar med 10 procent så minskar antalet brott per invånare med 0,5 procent.
Då risken för att åka fast ökar med 1 procent så minskar antalet brott per invånare med 5 procent.
- Spridningsdiagrammet nedan visar sambandet mellan genomsnittlig BMI och inkomst per person i olika länder. (BMI mäter relationen mellan vikt och längd. Högre värden betyder att man väger mer relativt sin längd. BMI-värden på 18,5-25 räknas som “normalviktig”; lägre värden som underviktig och högre som överviktig.) x-variabeln är inkomst per person i landet. En regressionslinje som beskriver sambandet ges av:
\[\widehat{BMI} = 12,55 + 1,43 \times ln(inkomst)\]
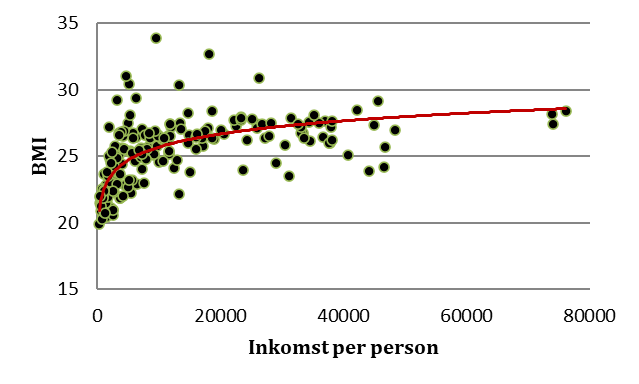
Den 10:e inkomstpercentilen är 1078 dollar per person. Prediktera BMI för ett land med denna inkomstnivå.
Den 90:e inkomstpercentilen är 35 247 dollar per person. Prediktera BMI för ett land med denna inkomstnivå.
I Finland är inkomsten 33 162 dollar per person. Hur hög predikteras genomsnittlig BMI vara i Finland?
Se fråga c: Genomsnittlig BMI i Finland är 26,73. Hur stor är Finlands residual?
Tolka koefficienten för ln(inkomst).
Dummy-variabler
- Tar man ut mindre sjukledigt inom privat sektor? För enkelhetens skull tänker vi oss här att vi samplat 13 sjuksköterskor varav 6 jobbar inom offentlig sektor och 7 inom privat. För varje person har vi mätt hur många dagar denna sjukskrivit sig under det senaste året. Data visas i datamatrisen nedan, där privat är en dummy som antar värdet 1 för personer som är anställda inom det privata och 0 annars; variabeln sjukdagar mäter antalet sjukskrivningsdagar.
| Id | Privat | Sjukdagar |
|---|---|---|
| 1 | 0 | 15 |
| 2 | 0 | 5 |
| 3 | 0 | 24 |
| 4 | 0 | 0 |
| 5 | 0 | 5 |
| 6 | 0 | 2 |
| 7 | 1 | 0 |
| 8 | 1 | 5 |
| 9 | 1 | 10 |
| 10 | 1 | 3 |
| 11 | 1 | 0 |
| 12 | 1 | 20 |
| 13 | 1 | 11 |
Vilka värden har a och b i regressionen: \(\widehat{sjukdagar} = a + b \times privat\)
- I en amerikansk studie jämförde man löner bland 534 arbetare varav 96 tillhörde facket. Data är för år 1985. Regressionslinjen ges av:
\[\widehat{lön} = 8,64 + 2,16 \times facket\]
där variabeln lön mäter arbetarens timlön; facket är en dummy som antar värdet 1 för fackanslutna och 0 för övriga. Hur stor är den genomsnittliga timlönen bland de fackanslutna? Bland dem som inte tillhör facket? Vad mäter koefficienten för facket?
- Nedan hittar du en sammanfattning av en artikel. Läs sammanfattningen och ge en tolkning av det som är understruket i rött:
Vad anger koefficienterna för x i dessa fall? (I artikeln betecknar man koefficienten för x med β.)
Vilken eller vilka av de tre x-variablerna är dummy-variabler? (“Hypertension” heter “högt blodtryck” på svenska.)

Det finns också andra sätt att beräkna regressionslinjer, men OLS är helt klart populärast. Om du ber ett statistisk programpaket ta fram en regressionslinje så använder den OLS per default.↩︎