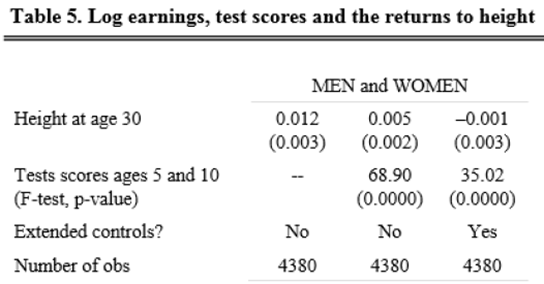
| Mått | Sampel: Estimat |
Population: Parameter |
Uttalet för de grekiska bokstäverna |
|---|---|---|---|
| Medelvärde | x̄ | μ | "my" |
| Proportion | p̂ | p | |
| Standardavvikelse | s | σ | "sigma" |
| Varians | s² | σ² | |
| Korrelation | r | ρ | "rho" |
| Regression | a, b (ŷ = a + bx) | α, β | "alfa", "beta" |
8 Statistisk inferens - the big picture
Alla kapitel hittills har handlat om hur man beskriver data. Men varför beskriver vi data? Dels kan det finnas ett självändamål i detta – vi vill helt enkelt lära oss om hur vårt datamaterial ser ut. Men huvudsyftet är oftast att generalisera. När vi gör generaliseringar utifrån data så kallas detta för statistisk inferens.
14. Statistisk inferens, del 1
15. Statistisk inferens, del 2
16. Statistisk inferens, del 3
8.1 Sampel kontra population
Om vi mäter priset för 100 fastigheter i huvudstadsregionen så vill vi inte enbart lära oss om priserna för de fastigheter som vi råkat välja ut, utan vi vill säga något generellt om prisläget på fastighetsmarknaden i den regionen. Det datamaterial vi har tillgång till kallas för ett sampel – detta är de 100 fastigheterna i exemplet ovan. Det här samplet kan ge oss en uppskattning av fastighetspriserna i regionen, t.ex. “i genomsnitt kostar fastigheterna 5328 euro per kvadratmeter”. Samplet kan däremot inte ge oss det exakta svaret; om vi upprepade studien med ett nytt urval fastigheter så skulle vi få ett annat resultat. Resultatet från ett sampel är därför osäkert. Men vi kan minska på osäkerheten genom att dra ett stort sampel; om vi mäter priset för 200 fastigheter istället för 100 så får vi ett säkrare resultat; och om vi mäter priset för 1000 fastigheter istället för 200 så får vi ett ännu säkrare resultat. Men först när vi samlat in data för alla fastighet i regionen så kan vi med säkerhet säga hur höga de genomsnittliga fastighetspriserna är. Den datamängd vi då har kallas för populationen.
Populationen är hela den datamängd som krävs för att vi ska få veta sanningen med fullständig säkerhet. Ibland kan vi betrakta populationen som alla enheter av intresse, t.ex. alla fastigheter i huvudstadsregionen. Här är ytterligare två exempel:
Exempel. Inför ett presidentval samplar vi 800 personer och frågar hur de tänkt rösta. Målet är att förutspå hur presidentvalet ska sluta. Populationen består då av alla röstberättigade medborgare som utnyttjar sin rösträtt, cirka tre miljoner personer; om vi hade ett datamaterial som täckte alla dessa personer så skulle vi med säkerhet veta hur presidentvalet slutar.
Exempel. Ett företag har 1218 anställda. Chefen vill veta hur många sjukdagar dessa tog ut under de 16 dagar som sommar-OS pågick år 2012. Populationen består då av dessa 1218 anställda; om företaget håller register över alla anställda och deras sjukskrivningar så kan chefen få ett säkert svar på sin fråga.
I de här exemplen består populationen av ett visst antal personer (alla som röstar, alla anställda). Men ibland kan populationen vara lite svårare att ta på än så. Som följande tre exempel visar så kan en population också vara oändligt stor:
Exempel. En tärning i Las Vegas tros vara riggad så att den ger för många sexor. Vi vill testa detta och kastar tärningen 1000 gånger. Dessa 1000 kast är nu vårt sampel. Hur många kast krävs det innan vi med säkerhet kan säga om tärningen är riggad eller inte? Det finns ingen övre gräns. Ytterligare ett kast skulle alltid kunna lära oss lite mer. Populationen är i detta fall oändlig.
Exempel. Vi vill ta reda på hur en viss medicin påverkar levervärdena hos möss. Vi testar medicinen på ett tiotal möss och uppmäter något försämrade levervärden. Detta betyder naturligtvis inte att vi nu har det fullständiga svaret. Hur många experiment måste vi göra förrän vi vet sanningen om medicinens effekt på levervärdena hos möss? Det finns ingen övre gräns. Ytterligare ett experiment skulle alltid kunna göra oss lite klokare. Också i detta exempel kan populationen ses som oändligt stor, och dessutom hypotetisk; just nu existerar det bara ett ändligt antal möss. (Men sett över tid så kommer det naturligtvis finnas en ständig ström av nya möss som vi hypotetiskt sett kunde experimentera med.)
Exempel. I ett aktiebolag är 8 av 20 styrelsemedlemmar kvinnor, trots att företaget anställer lika många män som kvinnor. Vilken slutsats kan vi dra av detta? Jo, vi kan med säkerhet säga att 40 procent av styrelsemedlemmarna är kvinnor. Om vårt mål är att ta reda på om kvinnor är underrepresenterade i företagets styrelse så besvarar detta vår fråga; populationen är då dessa 20 personer. Men låt oss säga att vi vill veta om kvinnor är systematiskt underrepresenterade: Finns det en underliggande process som tenderar att resultera i en skev könsfördelning i styrelsen? I så fall räcker det inte att veta att 8 av 20 är kvinnor; en sådan skillnad kan vara en ren tillfällighet (förra året kanske 12 av 20 var kvinnor). Det vi då egentligen vill veta är hur stor andel av styrelsemedlemmarna som skulle vara kvinnor sett över långa loppet.
Som de här exemplen visar så kan en population vara oändligt stor och till och med hypotetisk. Men vi kan ändå tänka oss att det finns en underliggande sanning som vi försöker lära oss om. Hur stor är medicinens sanna genomsnittliga effekt på levervärdena? Faller kvinnor systematiskt bort i valet av styrelsemedlemmar?
Estimat kontra parameter
Hittills har vi lärt oss om hur man beskriver sampel. Vi har använt mått såsom medelvärdet, variansen, korrelationer och regressioner. Nu ska vi introducera en ny idé; att alla dessa mått egentligen används för att uppskatta “det sanna medelvärdet”, “den sanna variansen”, “den sanna korrelationen” eller “den sanna regressionslinjen”, dvs. motsvarande mått i populationen. Vi kallar då de olika måtten i samplet (t.ex. samplets medelvärde) för ett estimat vilket är ett annat ord för en uppskattning. Det sanna värdet kallas för en parameter (t.ex. det sanna medelvärdet). Ofta använder man vanliga bokstäver för att beteckna estimat, medan man använder grekiska bokstäver för att beteckna parametrar. Tabellen nedan visar detta. Men det finns också undantag; proportionen i ett sampel betecknas oftast med \(\widehat{p}\) medan den sanna proportionen brukar betecknas med p.
Det som kännetecknar ett estimat är att det varierar från ett sampel till ett annat. Exempel: Om vi mäter det genomsnittliga priset för 100 fastigheter i huvudstadsregionen så är detta ett estimat; drar vi ett nytt urval fastigheter så kommer vi att få ett annat estimat. Det som kännetecknar en parameter är att den har ett konstant värde. Det genomsnittliga priset för alla fastigheter i huvudstadsregionen är ett exempel på en parameter. En parameter kan alltså inte ha olika värden beroende på vilka fastigheter vi råkar sampla eller beroende på utfallet i ett experiment; parametern beskriver ju en underliggande sanning.
Ibland när man bara talar om “ett medelvärde” eller “en varians” så kan det vara oklart om man avser estimatet eller parametern. Därför använder man ibland prefixet stickprovs- för estimat (stickprovsmedelvärdet, stickprovsvariansen, …). När man beskriver parametrar så kan man använda prefixet populations- (populationsmedelvärde, populationsvarians, …). Populations- medelvärdet brukar dessutom ofta benämnas väntevärdet eller det förväntade värdet.
8.2 Hypotesprövning
Du får höra att en ny studie visar att kvinnor i snitt kan hålla andan en minut längre än män. Kan det verkligen stämma? Låt oss säga att du nu får veta att enbart tre män och tre kvinnor ingick i den här studien. Du ser, det förklarar saken. När vi jobbar med sampel så finns det alltid en möjlighet att det mönster vi ser i data bara beror på slumpen; att skillnaden mellan könen inte är verklig. I det här kapitlet ska vi se hur vi kan ta ställning till om ett visst mönster i data är verkligt eller inte; kan mönstret bortförklaras av slumpen?
Nedan visas ett spridningsdiagram som representerar populationen eller sanningen. Vi har också ritat in populationens regressionslinje i diagrammet. Som du ser så är korrelationen mellan variablerna noll, \(\rho = 0\). Ett annat sätt att säga samma sak är att populationens regressionslinje har lutningen 0: \(\beta = 0\).
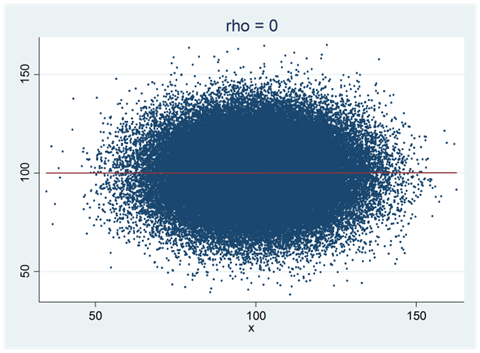
Nedan visas fyra spridningsdiagram med regressionslinjen utritad. Alla dessa sampel består av 100 observationer dragna från populationen ovan; en population där korrelationen är noll. Detta var de första fyra sampel jag råkade dra, och alla mönster som vi ser i dessa spridningsdiagram beror på slumpen.
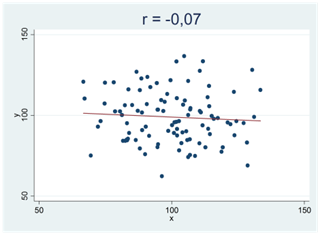
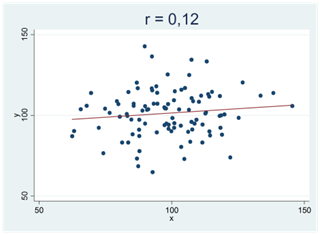
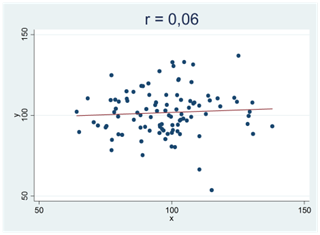
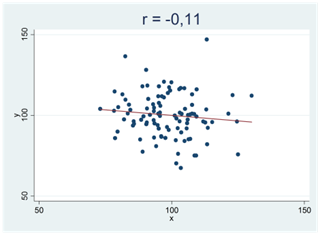
Här är något att tänka på: När du mäter korrelationen mellan två variabler i ett sampel så får du i princip aldrig en nollkorrelation, även då korrelationen mellan variablerna är noll i populationen. Varför? Av samma orsak som två stickprovsmedelvärden i princip alltid skiljer sig från varandra även om du drar samplen från samma population. Att två variabler korrelerar bevisar därför ingenting i sig självt. Att regressionslinjen lutar uppåt är på samma sätt inget bevis för att det faktiskt skulle finnas ett positivt samband mellan variablerna. Först när detta mönster blir tillräckligt tydligt, så tydligt att det inte kan bortförklaras av slumpen, kan vi påstå att sambandet är verkligt.
Här kan du testa din intuition. Nedan visas fyra spridningsdiagram (A, B, C och D). Två av de mönster som vi ser i figurerna nedan skulle mycket väl kunna bortförklaras av slumpen medan detta inte gäller för de andra två. Vilka två är detta?
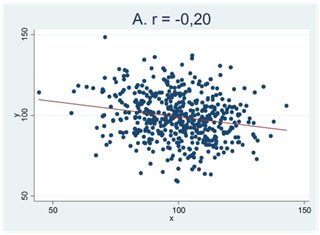
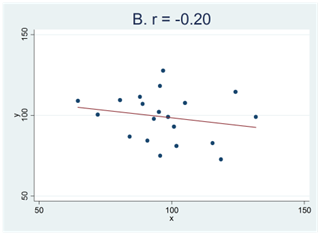
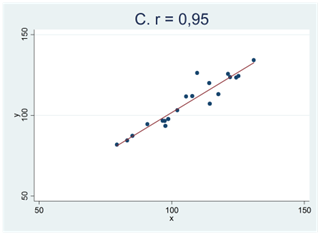
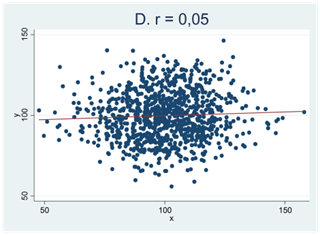
Om ditt svar är A och C så har du tänkt rätt. Mönstren i figur B och D skulle kunna skyllas på slumpen och de facto är detta också förklaringen; dessa sampel är dragna från populationer där korrelationen är noll. Detta gäller dock inte spridningsdiagram A och C.
När vi säger att mönstret i figur A och C “inte kan bortförklaras av slumpen” så är detta en sanning med modifikation. Alla mönster i data kan bero på slumpen. Men så pass tydliga samband som vi ser i figur C får man – av slumpen – enbart i 15 fall på en miljon försök. Vi har med andra ord ett mycket starkt stöd för att påstå att det här sambandet är verkligt; den andra möjligheten är att vi har råkat dra ett av de där 15 samplen – en försvinnande liten möjlighet. Man säger då att sambandet är statistiskt signifikant eller statistiskt säkerställt; vi har så att säga “säkerställt” att sambandet i data är verkligt. Oftast kräver vi dock inte såhär pass starka bevis; generellt gäller att vi kallar ett samband för signifikant om det hör till de 5 procent allra extremaste samband man kan få bara av slumpen. Ett exempel ges i spridningsdiagrammet nedan. Kan det här sambandet bortförklaras av slumpen? Nja, inte så lätt. Det här sambandet hör nämligen till de 2 procent extremaste samband som man kan få bara av slumpen. (Och eftersom det hör till de 2 procent extremaste så hör det också till de 5 procent extremaste.) Detta tyder på att mönstret i data är verkligt och vi skulle kalla sambandet för signifikant eller statistiskt säkerställt.
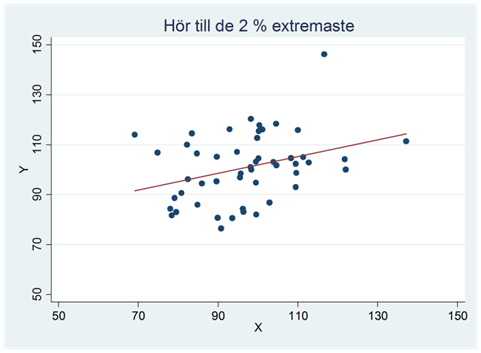
I det här skedet så kan det vara bra att fundera lite mer på vad vi menar med ett “extremt” samband, och hur vi kan mäta hur pass “extremt” ett visst samband är. För att göra detta så använder vi oss av test-statistikor.
Test-statistikor
En statistiska är ett samlingsnamn för alla mått som räknas utifrån observationerna i ett sampel. Stickprovsmedelvärdet är ett exempel på en statistiska (medan populationsmedelvärdet inte är det). En test-statistika är också ett mått som räknas utifrån observationerna i ett sampel. Vi kan tänka på en test-statistika som ett slags index som visar hur “extremt” ett visst sampel är. Test-statistikor kommer i lite olika varianter, men den mest använda är t-statistikan. T-statistikan antar allt större värden, positiva eller negativa, ju tydligare ett samband blir i data, dvs. ju svårare det är att skylla sambandet på slumpen.
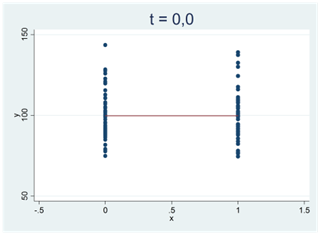
Se spridningsdiagrammet nere till vänster. Här är korrelationen 0,002 och regressionslinjen har lutningen 0,001. Det mycket svaga samband som vi ser i det här samplet skulle mycket väl kunna skyllas på slumpen. T-statistikan har därför ett värde nära noll: t ≈ 0,0. (Eller kortare: T-värdet är nära noll.) I diagrammet till höger har vi motsvarande situation. Här har vi ritat upp data för två grupper (x = 0 och x = 1). Gruppernas medelvärden är 99,72 och 99,73. Den här hårfina skillnaden skulle mycket väl kunna skyllas på slumpen; t-värdet är också här nära noll, t ≈ 0,0.
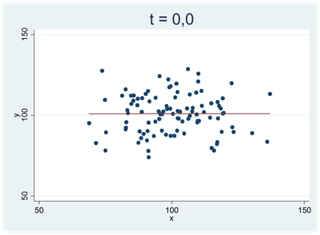
Ju svårare det är att bortförklara ett mönster i data med slumpen, desto mer avviker t-värdet från noll. Vi får stora positiva t-värden för tydliga och positiva samband; vi får stora negativa t-värden för tydliga och negativa samband. I spridningsdiagrammen nedan antar t-statistikan successivt allt större positiva värden:
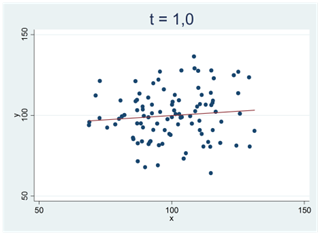
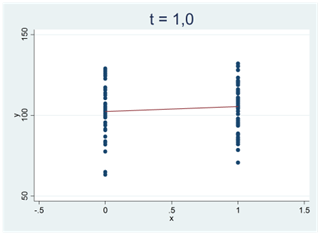
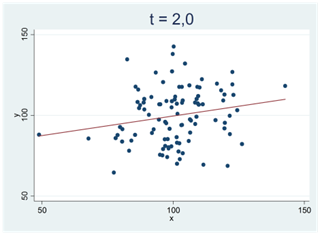
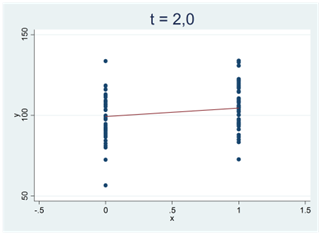
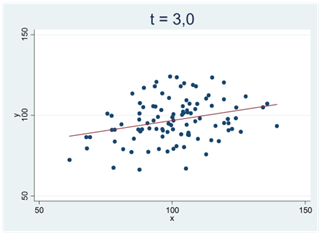
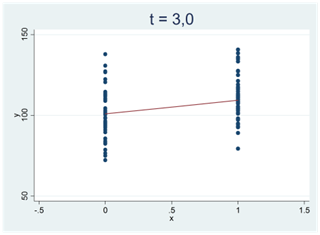
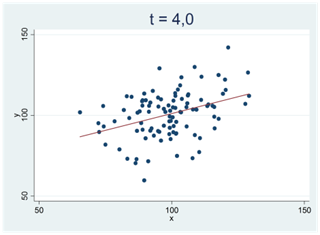
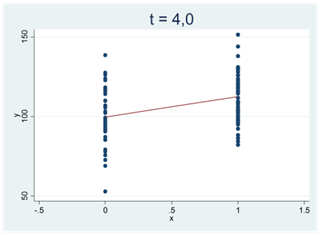
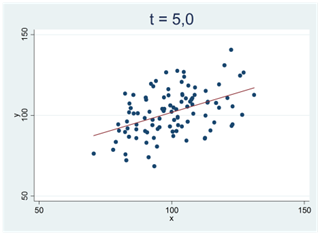
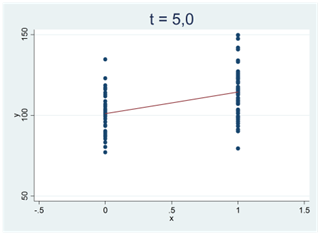
I spridningsdiagrammen nedan ser vi två tydliga och negativa samband; t-värdet är -5,0:
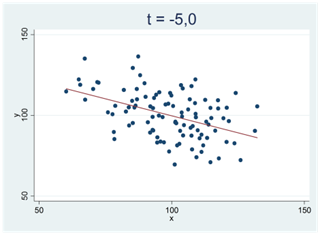
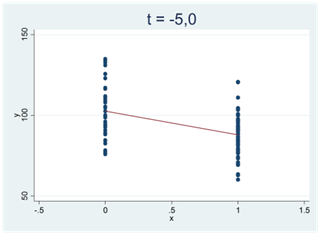
Det finns ingen gräns för stort värde t-statistikan kan anta (positivt eller negativt). Se samplet nedan. Det består av 100 000 observationer och korrelationen mellan variablerna är 0,99. Det här är ett mycket tydligt samband som svårligen kan skyllas på slumpen (vi skulle få dra biljontals och åter biljontals sampel innan vi fick ett såhär pass tydligt samband bara av slumpen). Här är t-värdet 2220.
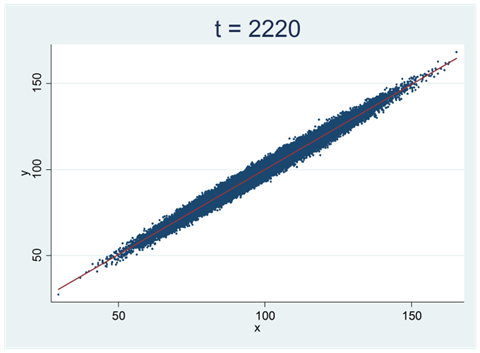
Man kanske kan få intrycket av att t-värdet är direkt knutet till storleken på korrelationskoefficienten eller regressionslinjens lutning. Detta är också riktigt, men det är inte hela historien. Jämför spridningsdiagrammen nedan. Bägge har samma korrelation (r = 0,37) men t-värdet är betydligt större i spridningsdiagrammet till höger, dvs. det är svårare att skylla det här sambandet på slumpen. Skillnaden mellan spridningsdiagrammen är samplets storlek; i diagrammet till vänster har vi 30 observationer; i diagrammet till höger har vi 300. Det här är också naturligt; om vi bara har ett fåtal observationer så är det lättare hänt att vi får ett ganska starkt samband i data bara av slumpen.
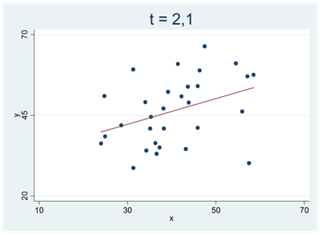
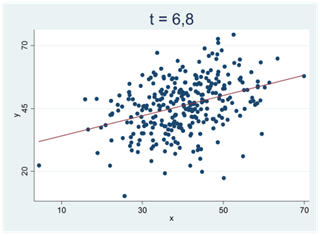
Exempel. Sover man mindre om man jobbar mycket? Spridningsdiagrammet nedan visar sambandet mellan jobb och sömn för ett sampel bestående av 706 amerikaner år 1974. Regressionslinjen ges av: \(\widehat{sömn} = 3586 - 0,15 \times jobb\), där sömn och jobb mäts i minuter per vecka: Då arbetstiden ökar med en minut så minskar nattsömnen i snitt med 0,15 minuter.
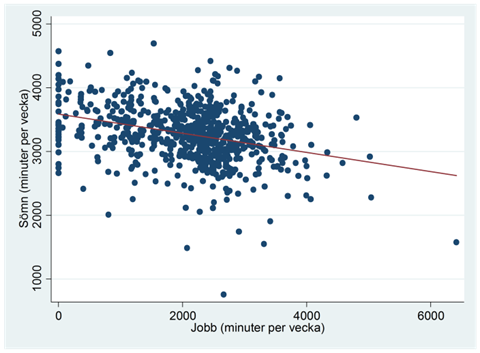
Vi ser att det här är ett tydligt samband; det verkar i det närmaste omöjligt att få ett såhär pass tydligt samband i data bara av slumpen. T-värdet är därför -9,0; ett värde som avviker mycket från noll. Om vi kör den här regressionen i ett statistiskt programpaket så hittar vi t-värdet i kolumnen “t”, på raden för variabeln jobb:
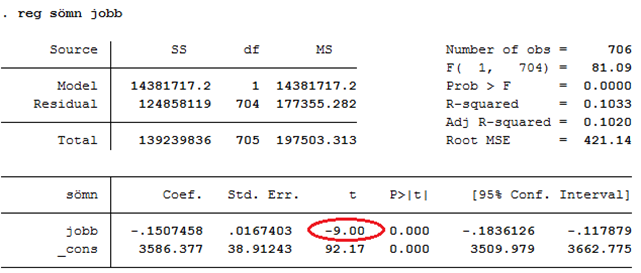
Som du ser finns det också ett annat t-värde i den här tabellen (92,17). Det här t-värdet är dock helt ointressant om vårt syfte är att ta reda på om sambandet mellan jobb och sömn är statistiskt signifikant; t-värdet av intresse hittas på raden för x-variabeln av intresse (jobb).
Hur t-värdet beräknas
T-värdet mäter effektens storlek men uttryckt i en annorlunda enhet. Vi uttrycker den nämligen i standardfel:
t-värdet = effektens storlek men uttryckt i antal standardfel
Så vad är ett standardfel? Ett standardfel är en standardavvikelse, men en speciell sorts standardavvikelse. Vi ser detta bäst genom ett exempel:
Se observationerna nedan. Här är standardavvikelsen ~0,57.
1,2 1,5 0,6 1,0 1,9 0,4 2,0 1,3
Men anta nu att dessa åtta värden är åtta koefficienter (b) från åtta regressioner som alla mäter samma samband. Orsaken till att koefficienterna har olika värden är att regressionerna är gjorda på åtta olika sampel. Standardavvikelsen (0,57) kallas då för ett standardfel för b.
Standardfelet för b visar hur mycket koefficienten varierar från ett sampel till ett annat då vi drar upprepade sampel, givet någon viss sampelstorlek. Ett stort standardfel betyder att koefficienten kastar mycket från ett sampel till ett annat; ett litet standardfel betyder att koefficienten är relativt stabil. Standardfelet kan därför ses som ett mått på osäkerheten i uppskattningen av den sanna effekten, β.
I praktiken har vi bara tillgång till ett sampel, vilket betyder att vi bara har en koefficient (b). Men det går också att beräkna standardfelet enbart utifrån ett sampel, dvs. vi kan använda samplet för att uppskatta hur mycket koefficienten skulle variera från ett sampel till ett annat om vi hade dragit upprepade sampel. En viktig ingrediens är samplets storlek; ju större sampel desto lägre standardfel (allt annat lika). Eller med andra ord: Ju större sampel desto stabilare koefficient från ett sampel till ett annat; om vi bara har ett fåtal observationer så är det lätt hänt att koefficienten kastar mycket från ett sampel till ett annat.
Man kan beräkna standardfel för vilka estimat som helst, och inte enbart för regressionskoefficienter. Principen är alltid densamma; standardfelet mäter hur mycket estimatet varierar från ett sampel till ett annat. Standardfelet för ett stickprovsmedelvärde mäter alltså hur mycket stickprovsmedelvärdet varierar från ett sampel till ett annat (givet någon viss sampelstorlek).
Exempel forts. Tidigare tittade vi på sambandet mellan jobb och sömn:
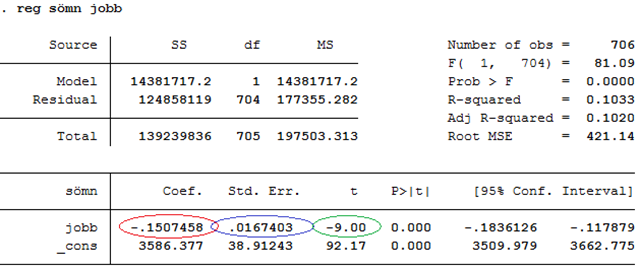
Effekten av jobb är -0,1507 minuter eller -9,0 standardfel (t = -9,0). Vi får t-värdet genom att dela effekten (-0,1507) med standardfelet (0,0167). I tabellen ovan är “Std Err.” kort för “Standard error”, dvs. standardfelet.
I en multipel regression får vi t-värden på motsvarande sätt. Anta nu att vi ännu kontrollerar för kön (dummyn man som antar värdet 1 för män och värdet 0 för kvinnor):
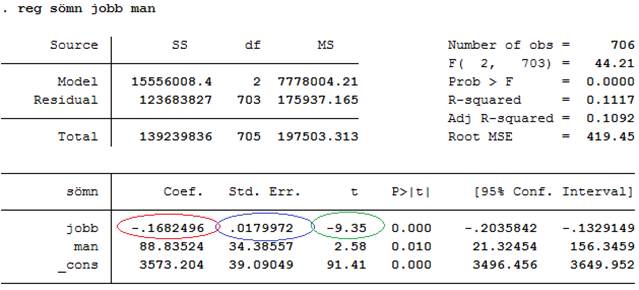
Effekten av jobb är nu -0,1682 minuter eller -9,35 standardfel (t = -9,35). T-värdet fås genom att dela effekten (-0,1682) med standardfelet (0,0180).
På motsvarande sätt ser vi att effekten av man är 88,8 minuter eller 2,58 standardfel.
Exempel. Är brottslingar dummare än befolkningen överlag? Vi låter 120 brottslingar göra ett intelligenstest. Intelligenstestet är konstruerat så att det har ett genomsnittligt värde på 100 i befolkningen överlag, µ = 100. Bland brottslingarna är den genomsnittliga intelligensen 96,0 poäng, och standardfelet för medelvärdet är 1,46 poäng.
Brottslingarna har alltså i snitt presterat 4 enheter sämre än befolkningen överlag (96 – 100 = -4). Men är det här en signifikant skillnad? Eller skulle den kunna skyllas på slumpen? I det här fallet är effekten -4 poäng eller -2,74 standardfel, dvs. t = -4/1,46 ≈ -2,74.
Ett t-värde på -2,74 räknas som ganska högt (absolut sett). Men är det tillräckligt högt för att skillnaden ska vara signifikant? Vi ska nu se närmare på den frågan.
P-värden
Vi kallar ett samband för signifikant om sambandet hör till de 5 procent allra extremaste samband som man kan få bara av slumpen. Vi använder test-statistikor för att mäta hur extremt ett samband är i det här avseendet. T-statistikan antar allt större värden (positiva eller negativa) ju svårare det att skylla sambandet på slumpen. Men hur stort värde bör t-statistikan anta för att sambandet ska kallas för signifikant? Jo, större än +2 eller mindre än -2. Om vi mäter ett samband och får ett t-värde på 2 (eller -2) så säger vi att p-värdet är 0,05: Sambandet hör till de 5 procent mest extrema samband som man kan få bara av slumpen.
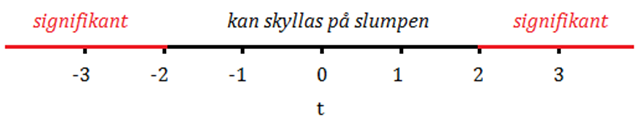
Ju större t-värde (positivt eller negativt) desto lägre p-värde. Om vi mäter ett samband och får ett t-värde på 3,0 så betyder det att p-värdet är ungefär 0,003: Sambandet hör då till de 0,3 procent mest extrema samband som man kan få bara av slumpen. Sambandet är med andra ord statistiskt signifikant.
När vi säger att t-värdet ska bli mindre än -2 eller större än +2 för att sambandet ska kallas signifikant så är detta en approximation. För stora sampel (~1000 observationer och uppåt) så ligger dessa gränser vid -1,96 och +1,96. För mindre sampel (~100 observationer) så ligger gränserna närmare -2 och +2. Gränserna varierar alltså med samplets storlek men närmar sig -1,96 och +1,96 då samplet blir allt större. Eller med anda ord: För ett stort sampel så betyder redan ett t-värde på 1,96 att p-värdet är 0,05. För ett mindre sampel så krävs det ett t-värde på 2,0 för att p-värdet ska bli 0,05.
För att få en bättre känsla för vad ett p-värde mäter så ska vi se på ett simuleringsexempel: Nedan visas ett spridningsdiagram som representerar populationen eller sanningen. Den sanna korrelationen är noll (\(\rho = 0\)) och regressionslinjen har lutningen noll (\(\beta = 0\)).
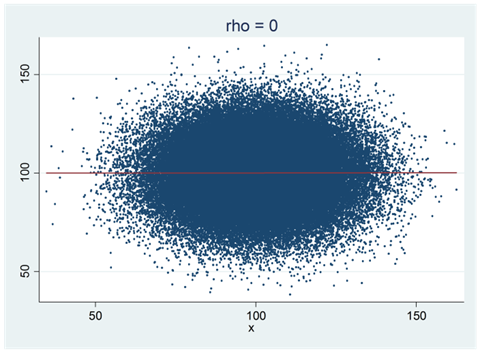
Vi drar nu ett sampel från den här populationen. Samplet visas i spridningsdiagrammet nedan och består av 100 observationer. t-värdet är -0,25.
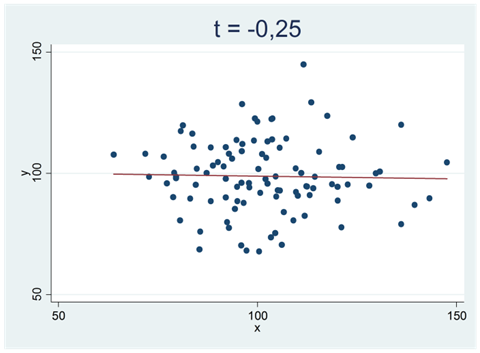
Vi upprepar nu detta experiment: Vi drar ytterligare ett sampel (100 observationer) och får ett nytt t-värde, denna gång 0,12. Och vi slutar inte här. Vi drar ett tredje sampel (100 observationer) och räknar ut ett tredje t-värde som blir -0,54. Så här kan vi fortsätta och dra ett sampel efter ett annat (alltid 100 observationer) och räkna ut nya t-värden för varje sampel. Här visas t-värdena från de första 10 samplen:
-0,25 0,12 -0,54 -0,58 -1,41 -0,71 1,24 0,12 1,44 -1,40
Men vi stannar inte heller här. Totalt drar vi 10 000 sampel och räknar ut 10 000 t-värden. Ett utdrag visas i tabellen nedan:
| Sampel # | t-värde |
|---|---|
| 1 | −0,25 |
| 2 | 0,12 |
| 3 | −0,54 |
| 4 | −0,58 |
| 5 | −1,41 |
| … | … |
| 100 | −0,50 |
| … | … |
| 1000 | −0,15 |
| … | … |
| 10000 | 1,03 |
Här har vi ritat upp fördelningen för alla 10 000 t-värden i ett histogram:
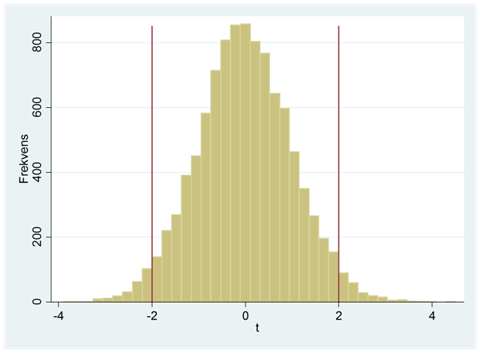
I ~95 procent av fallen har t-värdet hamnat någonstans mellan -2 och +2. Eller med andra ord: När sanningen är att det inte finns något samband mellan två variabler så får vi ett t-värde någonstans mellan -2 och +2 i 19 fall av 20 i långa loppet; i 1 fall på 20 får vi ett t-värde utanför detta intervall.
I sällsynta fall får vi t-värden som är extra stora (positiva/negativa). Ett av dessa 10 000 sampel gav exempelvis ett t-värde på 3,0. Vi har ritat upp detta sampel i spridningsdiagrammet nedan:
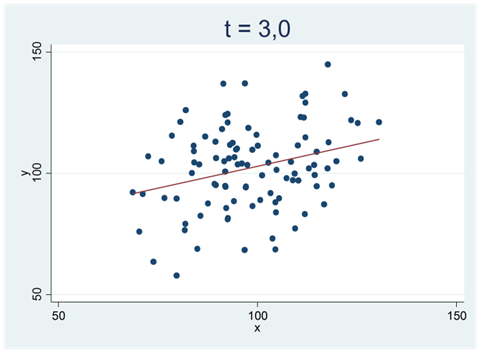
Hur ovanligt är det att få ett så här pass tydligt samband i data bara av slumpen? Kanske ovanligare än man skulle gissa. Histogrammet nedan visar att detta enbart hänt i några enstaka fall; av alla 10 000 sampel så är det totalt 34 som resulterat i ett t-värde på mindre än -3 eller större än +3. Med hjälp av en dator kan vi räkna ut den exakta sannolikheten; chansen för att få ett sampel där t-värdet blir mindre än -3 eller större än +3 är 0,3 procent. För det här samplet säger vi att p-värdet är 0,003: Detta samband hör till de 0,3 procent extremaste samband som man kan få bara av slumpen.
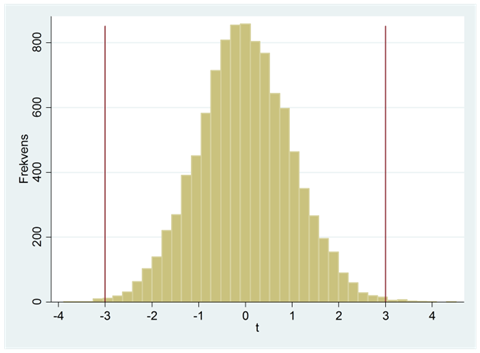
Ju lägre p-värde desto starkare stöd har vi för att påstå att sambandet i data är verkligt. Och när p-värdet blir mindre än 0,05 så kallar vi sambandet för signifikant.
Relationen mellan t-värdet och p-värdet
Relationen mellan t-värdet och p-värdet är inte helt enkel. Som vi har sett så betyder ett t-värde på 2,0 att p-värdet är ~0,05 men detta varierar också lite beroende på samplets storlek. Figuren nedan visar relationen mellan t-värdet och p-värdet; det att kurvan på sina ställen är lite tjockare reflekterar det att p-värdet varierar något beroende på samplets storlek.
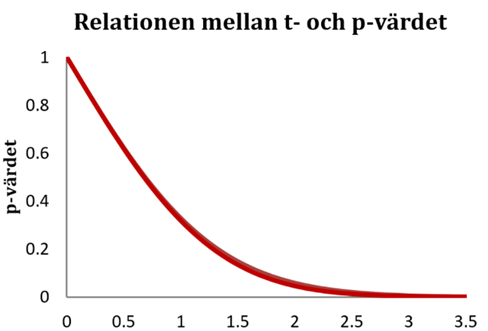
För normalstora sampel (~60 observationer och uppåt) så gäller:
| Absolutbeloppet av t-värdet |
p-värdet | |
|---|---|---|
| t > 1,7 | ⇒ | p < 0,1 |
| t > 2,0 | ⇒ | p < 0,05 |
| t > 2,7 | ⇒ | p < 0,01 |
Exempel. Tidigare tittade vi på hur nattsömn (sömn) varierar med arbetstid (jobb) och kön (man):
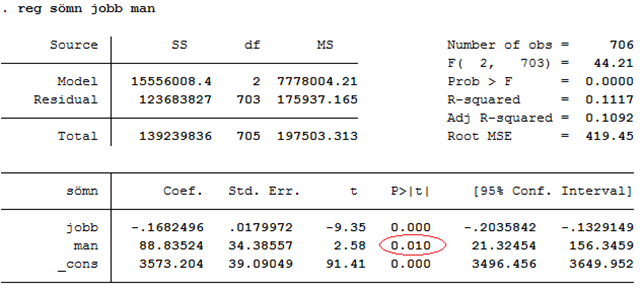
Vi ser att männen i data i snitt sover ~89 minuter längre än kvinnorna (kontrollerat för arbetstid). Men är skillnaden mellan könen signifikant? Ja, t-värdet är 2,58 vilket är större än 2; p-värdet är alltså mindre än 0,05. Från tabellen ovan ser vi att p-värdet egentligen är 0,010 (se kolumnen “P > |t|”). Det här sambandet hör alltså till de 1 procent extremaste som man kan få bara av slumpen. Vi har då ett starkt stöd för att påstå att sambandet är verkligt.
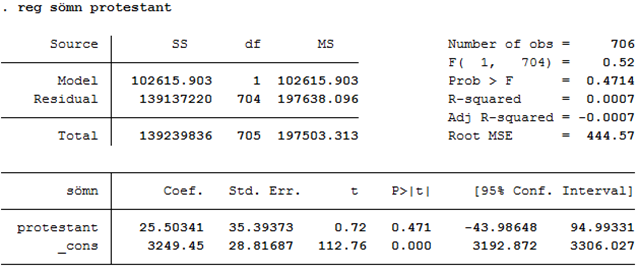
Exempel forts. I samma dataset finns också information om personernas religiösa bakgrund (dummyn protestant som antar värdet 1 för protestanter och värdet 0 för övriga). Sover protestanter längre än andra religiösa grupper? Ja, i vårt sampel sover protestanterna i snitt ~26 minuter längre (se utskriften nedan). Men skillnaden är inte signifikant. T-värdet är 0,72 vilket ger ett p-värde på 0,471. Det här sambandet hör alltså till de ~47 procent “extremaste” som man kan få bara av slumpen. Det här sambandet är alltså inte särskilt extremt alls. De facto ser det här samplet precis ut så som man kunde förvänta sig om protestanter och övriga egentligen sover exakt lika länge i genomsnitt. Vi säger då att sambandet är insignifikant.
Varför 5 procent?
Om p-värdet blir mindre än 0,05 så kallar vi ett samband för signifikant. Men varför dra gränsen vid just 5 procent? Det finns faktiskt ingen bra orsak. “5 procent” har blivit en tradition, men det är mer eller mindre en godtyckligt vald gräns; det finns ingen kvalitativ skillnad mellan ett p-värde på 0,051 och ett p-värde på 0,049. Om man vill vara lite mer nyanserad så kan man istället tala om att något är signifikant på en viss nivå:
Sambandet är signifikant på 10-procentsnivån ↔︎ p-värdet mindre eller lika med 0,1.
Sambandet är signifikant på 5-procentsnivån ↔︎ p-värdet mindre eller lika med 0,05.
Sambandet är signifikant på 1-procentsnivån ↔︎ p-värdet mindre eller lika med 0,01.
Ibland talar man också om att ett samband är “på gränsen till signifikant” (engelska: borderline significant) vilket betyder att p-värdet ligger någonstans mellan 0,05 och 0,1.
Noll- och mothypotes
Det här delkapitlet har titeln “Hypotesprövning”. Det vi har gjort här är att vi testat hypoteser, men vi har egentligen aldrig hänvisat till dem mer direkt. Så vilka är dessa hypoteser?
När vi mäter ett samband i data så finns det alltid två möjligheter: Antingen så finns det inget egentligt samband och det samband vi ser i data beror på slumpen. Eller så är sambandet verkligt. Vi kallar dessa två motstridiga möjligheter för noll- och mothypotesen:
Nollhypotesen: Inget samband (ingen effekt)
Mothypotesen: Samband (effekt)
När vi säger att ett samband är signifikant så kan vi också säga att vi “förkastar nollhypotesen”: Vi har bra stöd i data för att påstå att det finns ett samband. När vi säger att ett samband är insignifikant så kan vi också säga att vi “inte förkastar nollhypotesen”; det kanske finns ett samband eller så inte, men vi har inte tillräckligt med stöd i data för att säga att det finns ett samband.
Beroende på situation kan vi också uttrycka noll- och mothypotesen ovan på lite olika sätt.
På “regressionsspråk”:
Nollhypotesen: β = 0 (den sanna effekten är 0). Om vi mäter sambandet mellan två variabler så är detta samma sak som att säga att \(\rho = 0\) (den sanna korrelationen är 0). Mothypotesen blir då att β ≠ 0 eller att \(\rho \neq 0\).
Om x-variabeln är en dummy så kunde vi också uttrycka noll- och mothypotesen som följer:
Nollhypotesen: Populationsmedelvärdena i de två grupperna är lika stora, \(\mu_{0} = \mu_{1}\). Mothypotesen blir då att populationsmedelvärdena inte är lika stora, \(\mu_{1} \neq \mu_{0}\)
Vi ska ännu se på ett exempel:
Exempel. Är brottslingar dummare än befolkningen överlag? Vi låter 120 brottslingar göra ett intelligenstest. Intelligenstestet är konstruerat så att det har ett genomsnittligt värde på 100 bland befolkningen överlag (µ = 100). Bland brottslingarna är den genomsnittliga intelligensen 96,0 poäng, och standardfelet för medelvärdet är 1,46 poäng.
Nollhypotesen: Inget samband (brottslingar är varken dummare eller smartare än folk överlag). Eller med andra ord: Populationsmedelvärdet är också 100 bland brottslingarn, µb = 100. Mothypotesen blir då att det finns ett samband: µb ≠ 100.
I det här fallet blir t-värdet -2,74 och p-värdet blir 0,007. Brottslingarna har alltså signifikant lägre intelligenskvot än befolkningen överlag (0,007 < 0,05). Eller med andra ord: Vi kan förkasta nollhypotesen om att brottslingar har en genomsnittlig IQ på 100.
8.3 Konfidensintervall
Exempel forts. Nyss konstaterade vi att brottslingar har signifikant lägre IQ än befolkningen överlag. Men hur stor är skillnaden? I vårt sampel presterade brottslingarna i snitt 96 poäng på intelligenstestet. Men sanningen kunde ju mycket väl vara att snittet egentligen ligger vid 97 eller 95 poäng. Går det att ringa in sanningen, dvs. visa var det sanna medelvärdet ligger med stor säkerhet? Svaret är ja. Detta är vad konfidensintervall gör.
I det här fallet så ges ett 95-procentigt konfidensintervall för µ av: (93,1, 98,9). Det här betyder att sanningen ligger inom intervallet med 95-procentig säkerhet. Eller med andra ord: Brottslingarnas populationsmedelvärde ligger någonstans mellan 93,1 och 98,9 poäng med 95-procentig säkerhet.
Vi kan få fram ett ungefärligt 95-procentigt konfidensintervall genom att ta estimatet plus/minus två standardfel. I det här fallet är estimatet 96,0 och standardfelet är 1,46:
Konfidensintervallets nedre gräns: \(96,0 - 2 \times 1,46 \approx 93,1\)
Konfidensintervallets övre gräns: \(96,0 + 2 \times 1,46 \approx 98,9\)
Det går att göra upp konfidensintervall för vilka parametrar som helst. Vi ska nu se ett exempel på ett konfidensintervall för populationens regressionskoefficient.
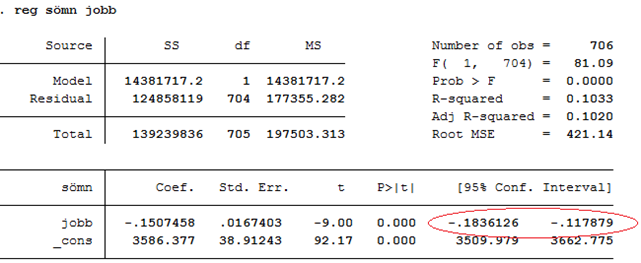
Exempel forts. Tidigare såg vi att det fanns ett signifikant samband mellan jobb och sömn. Regressionskoefficienten (b) har värdet -0,151: Då arbetstiden ökar med en minut så minskar nattsömnen med 0,151 minuter. Standardfelet för koefficienten är 0,0167. Ett 95-procentigt konfidensintervall för β ges då av (-0,184, -0,118), dvs. estimatet plus/minus två standardfel:
Nedre gränsen: \(- 0,151 - 2 \times 0,0167 \approx - 0,184\)
Övre gränsen: \(- 0,151 + 2 \times 0,0167 \approx - 0,118\)
Den sanna effekten (β) ligger alltså någonstans mellan -0,184 och -0,118 med 95-procentig säkerhet.
I regressionsutskriften nedan ges konfidensintervallets nedre och övre gränser i kolumnen “95 % Conf. Interval”.
Det typiska är att göra upp just 95-procentiga konfidensintervall. Men det går också att välja en lägre eller högre konfidensgrad. Ett 90-procentigt konfidensintervall innehåller sanningen med 90-procentig säkerhet; ett 99-procentigt konfidensintervall innehåller sanningen med 99-procentig säkerhet.
Så varför inte alltid rapportera 99-procentiga konfidensintervall (dessa är ju säkrare)? Kostnaden är intervallets bredd; ju större säkerhet desto bredare intervall. Ett 100-procentigt konfidensintervall är på det viset helt meningslöst; det skulle innefatta alla möjliga värden för parametern.
8.4 Antaganden
I vetenskapssammanhang pratar man ibland om “the black box” bakom ett fenomen. Med det menar man att man vet att något funkar (att en viss policy har effekt; att en viss medicin gör folk friska; att romarriket gick under för 1500 år sedan) men att det är oklart varför. Svaret på frågan varför ligger så att säga i en svart låda. Det här kapitlet har knappt alls berört den svarta lådan bakom statistisk inferens. Vi har bara sagt att det är såhär det funkar, men väldigt lite om varför. Här är några av de större frågorna som vi zappat förbi: Hur räknar vi ut ett populationsmedelvärde eller en sann regressionslinje? Och i synnerhet: Hur räknar vi ut dessa mått om vi har en oändligt stor population? (Jo, det går!) Varför funkar t-statistikan? När har man intresse av andra test-statistikor? Vi kommer att se på dessa frågor och flera andra under kommande kapitel; vi ska så att säga ta oss tid att öppna den svarta lådan.
Men det finns en sak som är värd att diskutera redan nu: Allting är approximationer. Då vi gör ett statistiskt test så spottar datorn ut ett p-värde och ett konfidensintervall. Men dessa är ungefärliga. Säg att vi får ett p-värde på 0,046. Det är då mycket möjligt att p-värdet egentligen borde vara 0,047. Och när vi gör upp ett konfidensintervall så heter det att “sanningen ligger inom intervallet med 95-procentig säkerhet”. Men det är mycket möjligt att sanningen egentligen ligger inom intervallet med 94-procentig säkerhet. De p-värden och konfidensintervall som datorn spottar ut är ungefärliga. (För att vara korrekt; det finns också så kallade exakta tester som ger exakta p-värden. Men det är ganska sällan som vi har tillfälle att använda dessa.)
Varför är våra tester och konfidensintervall ungefärliga? Jo, de bygger på vissa antaganden. (Vi ska inte gräva ner oss i dessa nu, men i det här skedet är det bra att veta att de finns.) Om vi synar dessa antaganden i sömmarna med en matematisk stränghet så kommer vi att märka att de faktiskt aldrig är hundraprocentigt uppfyllda. Det här kan låta illa, men är inte så farligt som det låter; det har sällan någon praktisk betydelse att datorn ger ett p-värde på 0,047 fastän det egentligen borde vara 0,046. Men säg att vi får ett p-värde på 0,047 fastän det egentligen borde vara 0,200. Det skulle ha praktisk betydelse. Kan det bli så pass fel? Svaret är ja.
Så nu blir frågan: När blir det såhär fel? Jo, alla de tester vi tittat på hittills bygger på antagandet om att vi har oberoende dragningar. Det är i synnerhet då detta antagande inte stämmer som det kan gå riktigt fel. Så vad menas då med oberoende och beroende dragningar? Vi ser detta bäst genom ett exempel:
Exempel. Den svenska reality-såpan FCZ bygger på idén om att nördar är dåliga fotbollsspelare. Programmet går ut på att en känd fotbollsspelare tränar med ett gäng “nördar” och i slutet spelar de en match mot Djurgården. Men är nördar dåliga fotbollsspelare? Kanske ligger det något i det. Vi har experimenterat med att låta nördar och “övriga” skjuta mot ett mål på 30 meters avstånd. Data visar antalet träffar (1) och missar (0):
Nördarna: 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1
Övriga: 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 1, 1, 1, 0
Bland nördarna har vi 2 träffar av 22. Bland “övriga” har vi 11 träffar av 22. Detta ser definitivt ut som en signifikant skillnad. Men låt oss nu säga att bland nördarna var alla skott förutom ett gjorda av Pelle (här utmärkt i rött):
Nördarna: 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1
Övriga: 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 1, 1, 1, 0
Vi ser nu att det är fel att påstå att nördar är sämre på fotboll. Snarare visar experimentet att Pelle är dålig på fotboll. Det här visar vad som menas med beroende mätningar; att Pelle skjutit de första 21 skotten gör dessa mätningar beroende, dvs. de hänger ihop.
I det här exemplet känner vi kanske intuitivt på oss att det är fel att behandla detta datamaterial precis på samma sätt som om alla Pelles skott vore skjutna av olika personer. Men ibland är det inte lika uppenbart. Tänk dig istället följande situation. Skotten är skjutna av olika nördar, men om en person träffar så höjer detta stämningarna så att nästa sannolikt också träffar; om en däremot missar så sänker detta stämningarna så att nästa sannolikt också missar. Data för nördarna kunde då se ut såhär:
Nördarna: 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 0, 0
Återigen har vi beroende mätningar; observationerna hänger ihop; utfallet på ett skott hänger samman med utfallet på föregående. Det fenomen som vi ser här är något som ofta karaktäriserar tiddseriedata (exempel: försäljningen ett år hänger samman med försäljningen föregående år).
Då vi jobbar med tvärsnittsdata så finns det i synnerhet ett tillfälle då dragningarna tenderar vara beroende. Detta inträffar då vi har dragit ett klustrat sampel. Klustrade sampel fås genom att först sampla grupper och därefter ta med alla (eller ett urval) enheter från varje grupp. Exempel: Vi vill studera lönenivåer bland industriarbetare. Först samplar vi ett antal företag inom branschen och därefter tar vi med alla (eller ett urval) arbetare från varje samplat företag. Exempel: Vi vill mäta hur mattebetyg varierar med lärarens arbetserfarenhet. Först samplar vi ett antal klasser och därefter tar vi med eleverna från varje samplad klass. Exempel: Vi vill undersöka graden av läskunnighet bland invånarna i en afrikansk stam. Först väljer vi slumpmässigt ut ett antal byar; därefter samlar vi in data för personerna i de samplade byarna.
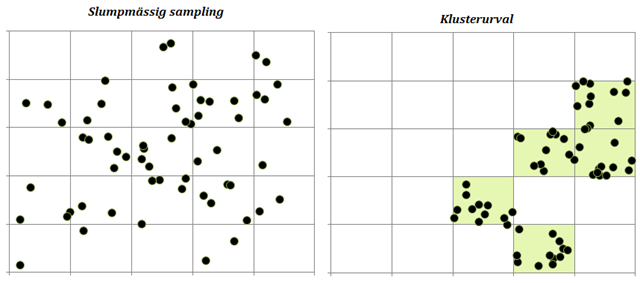
Figuren nedan illustrerar varför vi generellt sett inte kan behandla klustrade sampel på samma sätt som om vi valt personerna helt slumpmässigt. Vi kan tänka oss att rutfälten nedan representerar en stad bestående av 25 stadsdelar. Figuren till vänster representerar ett slumpmässigt sampel av stadsborna. I figuren till höger har vi istället slumpmässigt valt ut fem stadsdelar och därefter samlat in data för personerna i de samplade stadsdelarna. Bägge samplen består av 60 observationer, men det slumpmässiga samplet är mer representativt för staden i sin helhet. Det är som om det klustrade samplet egentligen innehöll färre observationer än det gör. Om vi inte beaktar detta så blir resultaten från de statistiska testerna missvisande.
När vi säger att det är ett antagande att vi har oberoende dragningar, så vore det kanske korrektare att säga att detta är ett antagande som vi gör när vi använder default-funktionerna på statistiska programpaket. Man gör alltså inget “statistiskt fel” om man drar ett klustrat sampel, men då måste man också beakta samplingstrategin. På samma sätt gör man naturligtvis inget statistiskt fel om man jobbar med tidsseriedata, men ibland blir då de p-värden som programmet ger (per default) lite fel. Vi kan dock justera för samplingstrategin då vi testar hypoteser. Hur detta går till i praktiken lämnar vi dock till senare.
Sammanfattning
Övningsuppgifter
Sampel kontra population
- Nedan beskrivs fyra frågeställningar. Ange om populationen är ändlig eller oändlig i respektive fall. Om ändlig, beskriv också vem eller vad som ingår i populationen.
Du vill ta reda på om de kvinnliga anställda på ett visst företag tagit ut mer övertid än männen under det senaste året. För att ta reda på detta samlar du in data för ett urval anställda och deras övertidstimmar.
En företagare ska skicka iväg en beställning bestående av 1000 rosor till en kund. Företagaren vill ta reda på hur god kvalitet dessa rosor håller och samplar slumpmässigt ett antal för testning.
Du vill ta reda på om den vinnande lottoraden de facto dras slumpmässigt så att alla sifferkombinationer har samma chans att bli dragna. Du samlar in historiska data över vinnande lottorader under de senaste 20 åren.
Du vill ta reda på om energidrycker höjer pulsen. Du låter hundra försökspersoner dricka en energidryck och uppmäter något förhöjda pulsvärden.
- Nedan ges beskrivningar av två olika studier. Vad är parametern av intresse i studien? Vad är estimatet? (Ange svaren skilt för respektive fall.)
Forskare studerar skallstorleken i ett sampel bestående av 28 vuxna neandertal-kranier. Syftet är att lära sig om väntevärdet för skallstorleken i populationen av alla neandertalare. Den genomsnittliga skallstorleken i samplet uppmättes till 1500 kubikcentimeter.
Politikerna vill ta reda på hur stor andel av finska kvinnor som ställer sig positiva till surrogatmödraskap. De samplar därför slumpmässigt 500 kvinnor och finner att 225 av dessa är positiva.
Hypotesprövning
- Se spridningsdiagrammen nedan (A, B och C). Alla tre samband har samma korrelation och samma regressionslinje (r = 0,10). Vi vill testa om sambandet mellan variablerna är signifikant.
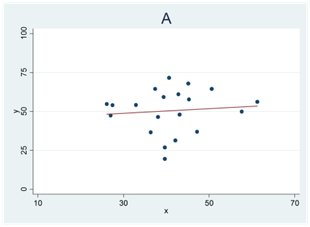
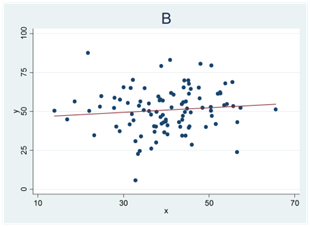
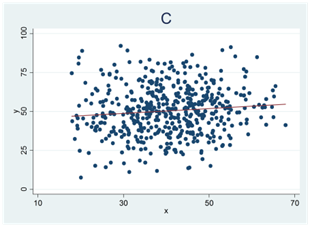
För vilket sampel (A, B eller C) är t-värdet som störst? För vilket sampel är t-värdet som lägst?
Enbart för ett av samplen är sambandet signifikant. Vilket?
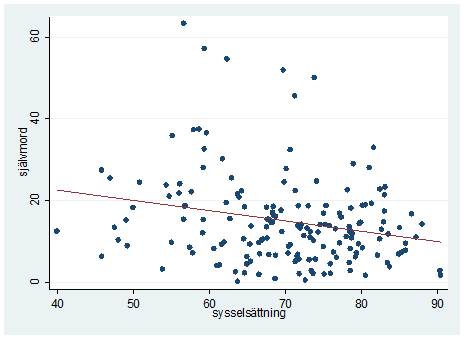
- Spridningsdiagrammet nedan beskriver sambandet mellan sysselsättningsgrad och självmordsfrekvens bland män i 169 länder. Du vill testa om sambandet är signifikant och får ett t-värde på -3,10. Vilken slutsats kan du då dra? Förklara kortfattat.
- Har ungdomar med ADHD sämre arbetsminne än ungdomar överlag? (Arbetsminnet är en persons korttidsminne och kan mätas som antalet siffror en person kan hålla i minnet samtidigt.) Bland ungdomar överlag ligger det genomsnittliga arbetsminnet på 7 siffror: µ = 7. Tabellen nedan beskriver data för ett slumpmässigt sampel omfattande 50 ungdomar med ADHD.
| Numbers recalled correctly | |
|---|---|
| Mean | 6.34 |
| Standard Error | 0.163158 |
| Median | 6 |
| Mode | 6 |
| Standard Deviation | 1.153699 |
| Sample Variance | 1.33102 |
| Kurtosis | −0.71678 |
| Skewness | −0.21444 |
| Range | 4 |
| Minimum | 4 |
| Maximum | 8 |
| Sum | 317 |
| Count | 50 |
Beskriv noll- och mothypotesen.
Hur stort blir t-värdet av intresse?
Hur stort blir p-värdet? Välj ett av alternativen: 0,258, 0,025 eller 0,0002.
Är resultatet signifikant? I så fall, på vilken nivå?
- Tabellen nedan är hämtad ur artikeln Body mass index as indicator of standard of living in developing countries. Utfallet är BMI.
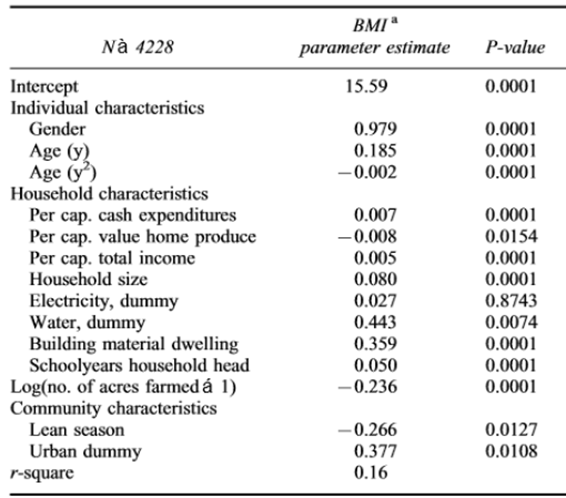
- Enbart en av de oberoende variablerna har inte en signifikant effekt på BMI. Vilken? Motivera kortfattat.
- Ge exempel på en effekt som är signifikant på 5-procentsnivån och en annan som är signifikant på 1-procentsnivån. (Ange de relevanta oberoende variablerna i ditt svar.)
- Tabellen nedan är hämtad ur artikeln Rooted in Poverty? Terrorism, Poor Economic Development, and Social Cleavages. Artikelns frågeställning: Vilka faktorer predikterar terrorism? Man använder data för 95 länder och mäter olika egenskaper hos länderna (ekonomiska, demografiska och politiska) och ser hur dessa relaterar till graden av terrorism. Graden av terrorism mäts som antalet terrorattacker under åren 1986-2002, samt antalet döda i terrorattacker under samma period. I tabellen nedan visas resultatet från två multipla regressionsanalyser (en för respektive utfall). Standardfel ges inom parentes; signifikanta effekter är utmärkta med en stjärna* och fetstil.
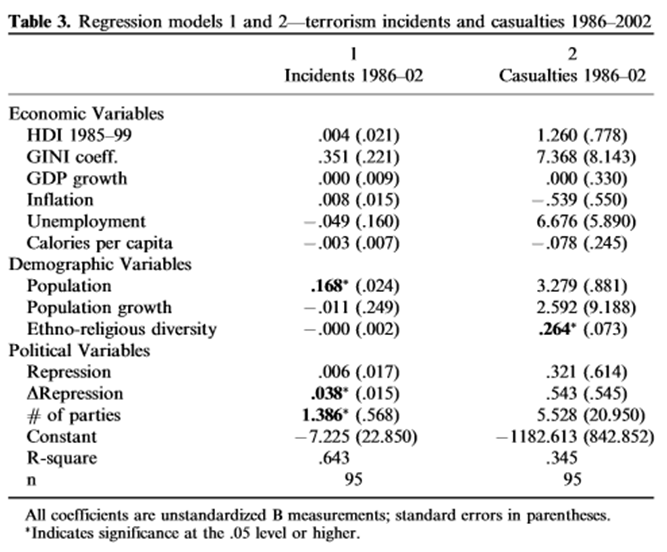
Från tabellen kan vi se att arbetslöshet (unemployment) inte har en signifikant effekt på antalet döda (casualties) medan effekten av etnisk-religiös mångfald (Ethno-religious diversity) är signifikant i samma regression. Bekräfta dessa slutsatser genom att räkna ut relevanta t-värden. Vad kan du säga om p-värdena och signifikansnivåerna i dessa fall?
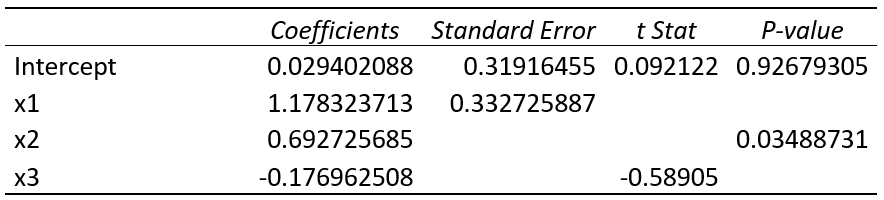
- Vi har kört en regression med y som utfall och tre oberoende variabler (x1, x2 och x3). Tabellen nedan sammanfattar resultatet. Vilken eller vilka av de tre effekterna är signifikanta? Motivera kortfattat.
- Nedan kan du läsa abstraktet till en artikeln The GCP Event Experiment: Design, Analytical Methods, Results. Artikeln beskriver ett högst kontroversiellt experiment. GCP står för “The Global Consciousness Project”. Projektet går ut på att mäta om mänsklighetens “globala medvetande” kan påverka utfallet i slumpgeneratorer (dvs. datorer som kastar ur sig siffror slumpmässigt). Hypotesen är att stora världsnyheter ska synas i slumpsiffrorna, dvs. påverka det slumpmässiga mönstret i data.

- Beskriv noll- och mothypotesen i den här studien.
- Författarna skriver att: “The cumulative significance across all events favors the hypothesis by more than 4.5 standard deviation.” Notering: Läs som “… 4,5 standardfel”. Är detta, statistiskt sett, ett starkt stöd för deras hypotes? Motivera kortfattat.
- Du vill mäta hur stor andel av alla studerande vid Åbo Akademi som jobbar vid sidan av studierna. Du samplar slumpmässigt 300 studerande varav 25 procent jobbar vid sidan av studierna, med ett standardfel på 2,5 procentenheter. Vilket eller vilka av följande påståenden är korrekta?
Om vi hade data över alla studerande vid ÅA så vore standardfelet 0.
Ju större sampel desto lägre standardfel (allt annat lika).
Standardfelet är ett mått på osäkerheten i uppskattningen av hur stor andel av studerande som jobbar vid sidan av studierna.
Konfidensintervall
- Nedan visas abstraktet till artikeln Associations with common health symptoms with bullying in primary school children. Understruket med rött ges några 95-procentiga konfidensintervall. Beskriv i ord vad det första konfidensintervallet betyder.

- Tabellen nedan är klippt ur artikeln Stature and Status: Health, Ability and Labor Market Outcomes. Utfallet är loggad lön (den naturliga logaritmen) och x-variabeln av intresse är längd (height, mätt i tum). Standardfel ges inom parentes. Se specifikationen som inte kontrollerar för testresultat i ung ålder eller övriga kontrollvariabler (extended controls). Gör upp ett ungefärligt 95-procentigt konfidensintervall för effekten av längd. Ge också en tolkning av detta konfidensintervall.