| Ort | Risk att åka fast | Brottslighet |
|---|---|---|
| 1 | 0,298270 | 0,035604 |
| 2 | 0,132029 | 0,015253 |
| 3 | 0,444444 | 0,012960 |
| 4 | 0,364760 | 0,026753 |
| 5 | 0,518219 | 0,010623 |
| … | … | … |
| 89 | 0,689024 | 0,018985 |
3 Sambandet mellan två variabler - korrelationer
I förra kapitlet lärde vi oss hur man beskriver fördelningen för en variabel. Oftast är vi dock intresserade av att studera sambandet mellan variabler. Vi ska nu se några exempel på vad vi egentligen menar med samband, och hur vi kan beskriva samband mellan två variabler med hjälp av korrelationsmått.
4. Korrelationer, del 1
5. Korrelationer, del 2
6. Korrelationer, del 3
3.1 Samband
Exempel. Finns det ett samband mellan etnisk bakgrund och hälsa? I National Health Interview Survey intervjuas tusentals amerikaner angående sin hälsa. Figuren nedan visar visar att cirka 60 procent av latinamerikaner och svarta anser sig ha mycket god hälsa; bland vita är motsvarande siffra cirka 70 procent.
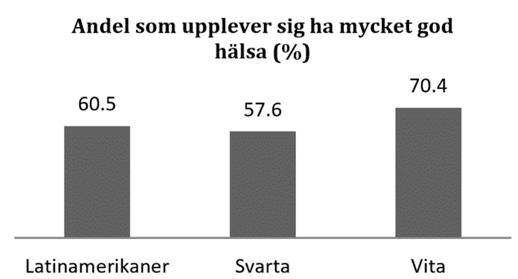
Så vad menar vi med ett samband? När vi säger att det finns ett samband mellan två variabler – x och y – så menar vi att kunskap om den ena variabeln (x) lär oss något om den andra (y). I exemplet ovan så finns det ett samband mellan etnicitet och hälsa; om vi vet personens etniska bakgrund så lär det oss något om personens hälsa. I det här fallet så skulle det inte finnas något samband mellan variablerna om andelen med mycket god hälsa var lika stor i alla tre grupper.
Exempel. Tjänar högutbildade mer än lågutbildade? Figuren nedan visar lönerna i tre utbildningsgrupper: personer med enbart grundskoleutbildning, personer med gymnasie- eller yrkesutbildning och sådana med högskole- eller universitetsutbildning.
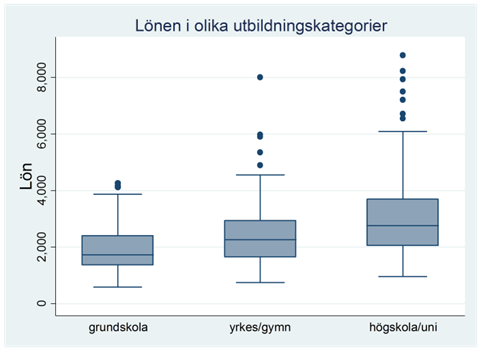
Som du ser så är lönerna jämförelsevis låga bland personer med enbart grundskoleutbildning, men betydligt högre bland personer med högskole- eller universitetsutbildning. Det finns också flera undantag – personer med grundskoleutbildning som tjänar tusenlappar mer än andra med högskoleutbildning – men den generella trenden i data är tydlig. Det finns med andra ord ett samband mellan utbildningsnivå och lön.
Hur kan vi karaktärisera detta samband? En viktig skillnad kan göras mellan positiva och negativa samband. Vi kallar ett samband för positivt då höga värden på en variabel (x) hänger samman med höga värden på en annan (y). Och tvärtom: Låga värden på x hänger samman med låga på y. Vi kallar ett samband för negativt då höga värden på en variabel (x) hänger samman med låga värden på en annan (y). Och tvärtom: Låga värden på x hänger samman med höga på y. I det här exemplet är sambandet positivt, dvs. en hög utbildningsnivå hänger samman med hög lön.
[Notering: Data för exemplet ovan är fejkat.]
Exempel. Begås det mindre brott om risken för att åka fast är hög? Vi mäter antalet brott per person och risken för att åka fast i 89 amerikanska orter. Ett utdrag av data ges nedan:
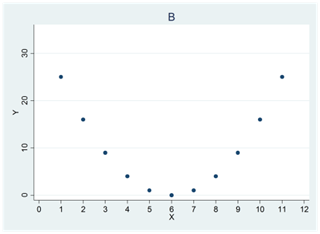
Figuren nedan illustrerar sambandet med hjälp av ett spridningsdiagram. På x-axeln visas risken för att åka fast; på y-axeln visas antalet brott per person. Varje “prick” i diagrammet representerar en observation, dvs. en ort. Exempelvis ser vi att det finns en ort där risken för att åka fast är ~0,7. På den orten begås det ~0,02 brott per person. I tabellen ovan är detta ort #89.
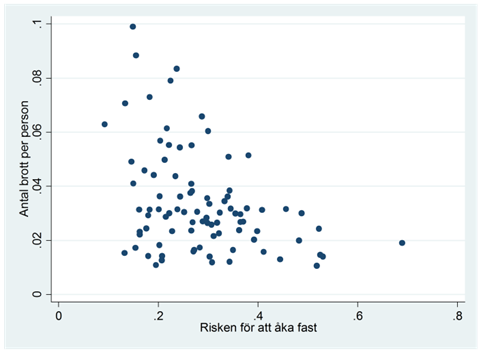
Vad visar spridningsdiagrammet? För det första ser vi att det finns ett samband mellan variablerna; brottsligheten skiljer sig systematiskt mellan orter där risken för att åka fast är hög och sådana där risken är låg. Vi ser också att sambandet är negativt; hög risk för att åka fast är förknippat med låg brottslighet.
Vi har sett att samband ofta kan karaktäriseras som positiva eller negativa. I kommande avsnitt ska vi fundera vidare på hur man kan karaktärisera samband genom att mäta styrkan i dessa. I detta syfte använder vi korrelationskoefficienter. Det finns olika sätt att mäta styrkan i ett samband, dvs. olika korrelationskoefficienter, men de flesta har följande gemensamt: De antar värden mellan -1 och 1, där 1 betyder att det finns ett perfekt positivt samband mellan variablerna och -1 att det finns ett perfekt negativt samband mellan variablerna; en korrelation på 0 betyder att det inte finns något samband (eller att sambandet varken är positivt eller negativt).
Så vad menar vi då med ett perfekt negativt eller positivt samband? Man kan här tänka sig lite olika betydelser och därför finns det också olika korrelationskoefficienter. I nästa avsnitt ska vi diskutera det vanligaste korrelationsmåttet: Pearsons korrelationskoefficient. När vi då talar om perfekta samband så menar vi linjära samband.
3.2 Pearsons korrelationskoefficient
Pearsons korrelationskoefficient är det vanligaste korrelationsmåttet. Den mäter styrkan i det linjära sambandet mellan två variabler och antar värden mellan -1 och 1, där positiva värden betecknar positiva samband och negativa värden negativa samband.
Se figur A nedan: Då x ökar så ökar också y i genomsnitt. Vi har då en positiv korrelation mellan variablerna. En korrelation på 1 betyder att alla observationer kan ritas längs med en uppåtlutande linje (figur B).
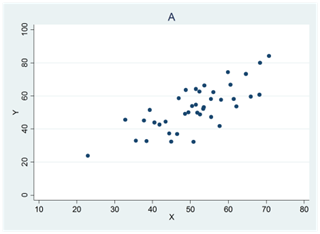
Se figur A nedan: Då x ökar så minskar y i genomsnitt. Vi har då en negativ korrelation mellan variablerna. En korrelation på -1 betyder att alla observationer kan ritas längs med en nedåtlutande linje (figur B).
Spridningsdiagrammen nedan representerar en korrelation på noll: Då x ökar så varken ökar eller minskar y i genomsnitt.
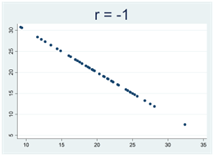
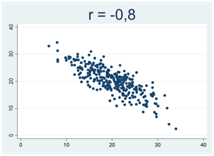
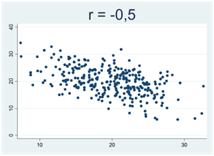
Generellt gäller att då korrelationskoefficienten närmar sig 1 eller -1 så samlas observationerna allt tajtare kring en rät linje. Figurerna nedan illustrerar detta, där r betecknar Pearsons korrelationskoefficient:
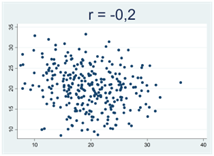
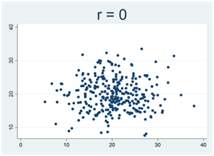
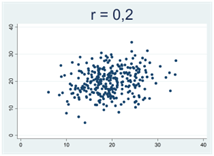
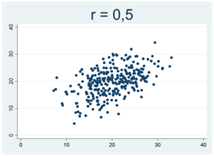
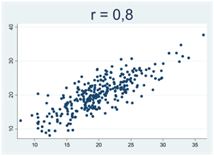
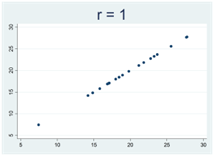
Hur Pearsons korrelationskoefficient beräknas
Korrelationen mellan två variabler, x och y, beräknas genom att dela kovariansen med produkten av standardavvikelsen för x och standardavvikelsen för y. Så vad är då kovariansen?
Kovariansen mellan x och y beskriver hur mycket variablerna svänger ihop. Vi betecknar denna med sxy:
\[s_{xy} = \frac{\sum_{}^{}{(x_{i} - \overline{x})(y_{i} - \overline{y}})}{n - 1} = \frac{\sum_{}^{}{x_{i}y_{i}} - n\overline{x}\overline{y}}{n - 1}\]
Som du ser så ges här två formler för kovariansen. Båda ger förstås samma resultat, men den senare är lättare att använda vid manuella beräkningar.
Exempel. Finns det ett samband mellan faderns och sonens inkomst? För enkelhetens skull tänker vi oss här att vi bara har fyra observationer, dvs. fyra par av fäder och söner. I tabellen nedan representerar x faderns inkomst och y sonens. Inkomsterna mäts i tusentals euro (så att värdet 1 representerar en inkomst på tusen euro). I snitt tjänar både fäder och söner 2500 euro: \(\overline{x} = \overline{y} = 2,5\). Hur stor blir kovariansen mellan faderns och sonens inkomst?
| x (far) | y (son) |
|---|---|
| 1 | 1 |
| 2 | 3 |
| 3 | 2 |
| 4 | 4 |
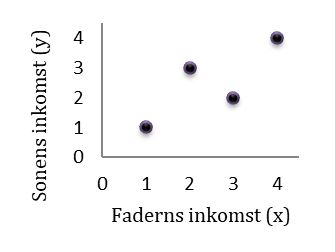
Vi kan börja med att beräkna \(\sum_{}^{}{x_{i}y_{i}} = x_{1}y_{1} + x_{2}y_{2} + x_{3}y_{3} + x_{4}y_{4}\) som finns i täljaren för kovariansen. Från tabellen nedan ser vi att denna summa blir 29:
| x (far) | y (son) | x · y |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 3 | 6 |
| 3 | 2 | 6 |
| 4 | 4 | 16 |
| Σ = 29 |
Kovariansen blir då 4/3:
\[s_{xy} = \frac{\sum_{}^{}{x_{i}y_{i}} - n\overline{x}\overline{y}}{n - 1} = \frac{29 - 4 \times 2,5 \times 2,5}{4 - 1} = \frac{4}{3}\]
Så vad betyder en kovarians på 4/3? En positiv kovarians betyder att det finns ett positivt samband mellan variablerna; en negativ kovarians att sambandet är negativt; en kovarians på noll betyder att det inte finns något linjärt samband.
I det här exemplet har vi en positiv kovarians, dvs. ett positivt samband. Därutöver är det svårt att tolka kovariansen; storleken beror också på vilka enheter vi använder för att mäta x- och y-variablerna. Men vi kan göra kovariansen enhetsfri genom att dela den med produkten av standardavvikelsen för x och standardavvikelsen för y. Det mått vi då får kallas för Pearsons korrelationskoefficient och betecknas med r:
\[r = \frac{s_{xy}}{s_{x} \times s_{y}}\]
I exemplet ovan gäller att standardavvikelsen för sonens och faderns inkomster är lika stora, och lika med \(\sqrt{5/3}\). Produkten av dem är 5/3. Korrelationen blir då 0,8 vilket representerar ett stark positivt samband:
\[r = \frac{s_{xy}}{s_{x} \times s_{y}} = \frac{4/3}{5/3} = 0,8\]
Vi ska här notera två egenskaper hos korrelationskoefficienten:
Det spelar ingen roll vilken variabel som är x, och vilken som är y. Om vi vände på det så att x var sonens inkomst och y faderns så skulle korrelationskoefficienten ändå få värdet 0,8.
Det spelar ingen roll vilka enheter vi använder för att mäta variablerna. Vi kunde exempelvis mäta faderns inkomst i euro och sonens i tusentals euro och ändå få korrelationen 0,8.
Icke-linjära samband och logaritmering
I spridningsdiagrammet nedan är korrelationen 0: Då x ökar så varken ökar eller minskar y i genomsnitt. Men den här beskrivningen av sambandet är rätt torftig, dvs. den säger mycket litet om hur sambandet de facto ser ut.
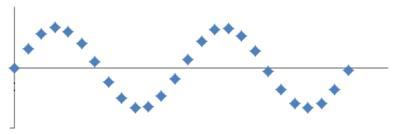
Generellt gäller att ju bättre ett samband beskrivs av en kurva istället för en linje, desto mindre informativt blir Pearsons korrelationskoefficient som mått. Vi ska nu se ytterligare exempel på detta:
Exempel. Spridningsdiagrammet nedan beskriver sambandet mellan inkomst och livslängd i världens länder. Inkomst mäts som inkomst per person i landet; livslängd är den genomsnittliga livslängden. Vi ser att livslängden i snitt är högre i rika länder än i fattiga. Det finns med andra ord en positiv korrelation mellan variablerna; Pearsons korrelationskoefficient har värdet 0,62. Men vi ser också att sambandet beskrivs bäst genom en kurva; då vi rör oss från de allra fattigaste länderna till något rikare länder så ökar livslängden dramatiskt, men efter 20 000 dollar finns det inte längre något samband att tala om; alla dessa länder har höga livslängder.
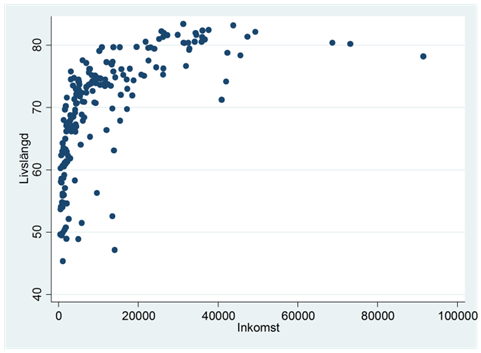
I det här exemplet gör Pearsons korrelationskoefficient ett ganska dåligt jobb med att beskriva sambandet mellan variablerna. Finns det något som vi kan göra för att förbättra den beskrivningen? En möjlighet är att ändra skalan på y- eller x-axeln så att sambandet blir linjärt. Logaritmering är det vanligaste sättet att åstadkomma detta.
Vi har tidigare sett att logaritmering innebär att vi beskriver variabeln på en ny skala. Om vi logaritmerar inkomsterna i exemplet ovan så får vi en skala där avståndet mellan 20 000 och 40 000 är lika stort som det mellan 40 000 och 80 000:
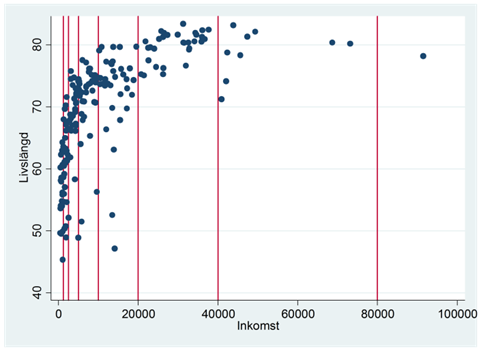
Detta ger oss följande spridningsdiagram:
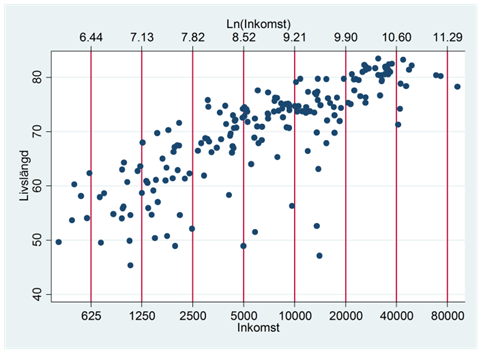
Vi ser att log-skalan ger oss ett datamaterial som bättre passar en rät linje:
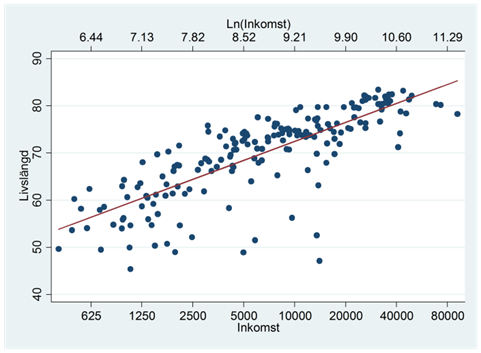
Vi beräknar sedan Pearsons korrelationskoefficient på samma sätt som tidigare, bara att x-variabeln nu är ln(inkomst) istället för inkomst. Ett utdrag av data ges nedan:
| land | inkomst | ln(inkomst) | livslängd |
|---|---|---|---|
| Afghanistan | 1 349,70 | 7,207638 | 60,524 |
| Albanien | 6 969,31 | 8,849272 | 77,185 |
| Algeriet | 6 419,13 | 8,767038 | 70,874 |
| Angola | 5 838,16 | 8,672171 | 51,498 |
| Antigua & Barbuda | 13 723,00 | 9,526829 | 75,783 |
| … | … | … | … |
| Finland | 31 552,00 | 10,359392 | 80,362 |
| … | … | … | … |
| Zimbabwe | 545,35 | 6,301419 | 58,142 |
Korrelationen mellan ln(inkomst) och livslängd är 0,79.
Man kan undra om det inte är fusk att ändra skalan på det här viset? Men nej, snarare är det tvärtom. När vi beräknar Pearsons korrelationskoefficient och använder den vanliga skalan så tänker vi oss att en viss ökning i inkomst hänger samman med en viss ökning i livslängd; med den logaritmiska skalan tänker vi oss istället att en viss procentuell ökning i inkomst hänger samman med en viss ökning i livslängd. Den logaritmiska skalan ger oss här en bättre representation av sambandet.
Så hur vet man om, och när, det är lämpligt att logaritmera en variabel? Och vilken eller vilka variabler ska man i så fall logaritmera? Här är tre tips:
- Logaritmering innebär att vi pressar ihop den axeln så att stora värden straffas extra hårt. Med hjälp av spridningsdiagram kan vi visualisera vilken axel det vore lämpligt att pressa ihop (dvs. logga) för att få ett linjärt samband.
Exempel. Se spridningsdiagrammet nedan. För vilken axel skulle en loggad skala vara lämplig?
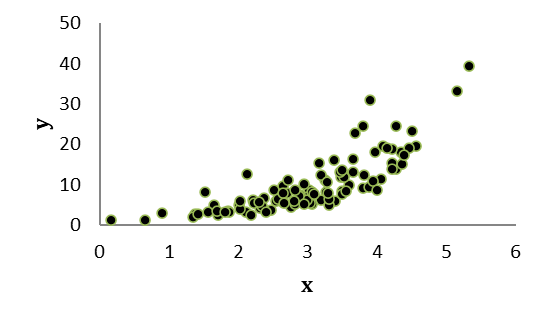
Om ditt svar är “y-axeln” så har du tänkt rätt. När vi logaritmerar y så får vi följande spridningsdiagram:
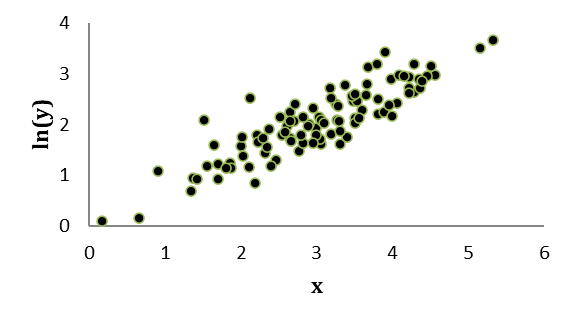
- Det är ofta lämpligt att logaritmera en variabel som har en fördelning med en längre svans till höger, dvs. ett antal extra höga värden.
Exempel. Om vi ritar upp fördelningen för inkomster i världens länder så ser vi att det är fallet här:
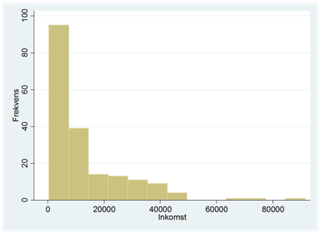
Variabler som mäts i pengar, i stora antal eller kvantiteter har som regel en längre svans till höger och sådana variabler brukar logaritmeras nästan rutinmässigt.
Exempel. Spridningsdiagrammet nedan visar sambandet mellan kroppsvikt och hjärnans vikt för 62 olika djurarter. Kroppsvikten mäts i kilo och hjärnans vikt i gram.
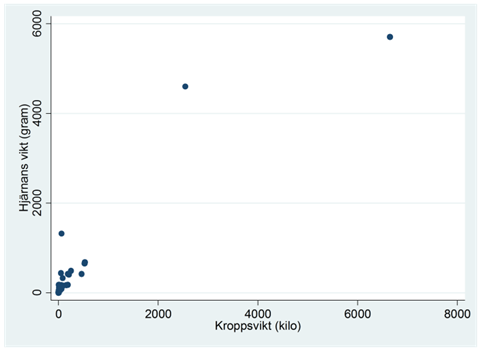
Från frekvensdiagrammen nedan ser vi att båda variablerna har fördelningar som är skeva till höger:
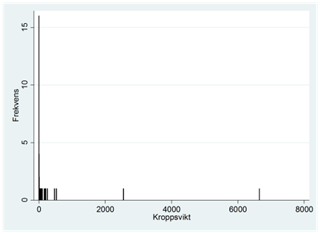
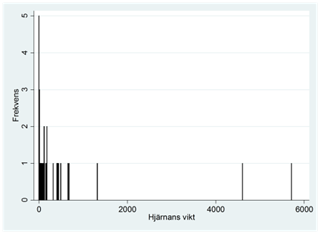
När vi använder en logaritmisk skala för dessa variabler så får vi ett linjärt samband. Här har korrelationskoefficienten värdet 0,96:
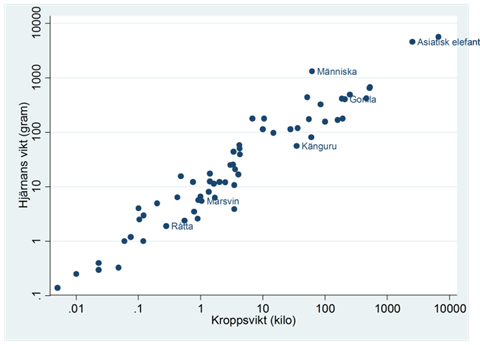
När vi använder den logarimiska skalan för både kroppsvikt och hjärnans vikt så tänker vi oss att en viss procentuell förändring i kroppsvikt hänger samman med en viss procentuell förändring i hjärnans vikt. Och som vi ser från spridningsdiagrammet ovan så är detta en bra beskrivning av sambandet. Grovt räknat så gäller att en ökning i kroppsvikten med en faktor på 10 hänger samman men en ökning i hjärnans vikt med en faktor på 10.
- Vi logaritmerar bara variabler för vilka det är meningsfullt att mäta förändringar i procent.
Detta utesluter alla variabler som antar negativa värden (negativa värden har ingen logaritm; detsamma gäller talet 0). Vi skulle exempelvis inte logaritmera temperaturen (mätt på en celsius-skala) för det är inte meningsfullt att tala om procentuella förändringar i temperatur; 16 grader är inte 60 procent varmare än 10 grader.
Vad är en bra korrelation?
Hur hög bör en korrelation vara för att vara “bra”? Är 0,6 en bra korrelation? Är -0,5 en bra korrelation? Svaret är att det inte finns några bra eller dåliga korrelationer. Vi använder korrelationskoefficienter för att beskriva ett mönster i data på motsvarande sätt som vi använder medelvärdet för att beskriva tyngdpunkten i en fördelning. Och på samma sätt som det inte finns några medelvärden som är bättre än andra, så finns det heller inga korrelationskoefficienter som är bättre eller sämre än andra. Men medelvärdet kan ge en haltande beskrivning av en variabels läge då fördelningen är skev; på motsvarande sätt kan också Pearsons korrelationskoefficient ge en haltande beskrivning av förhållandet mellan två variabler då förhållandet är icke-linjärt. I det här avsnittet har vi sett hur vi kan använda en logaritmisk skala för att göra sambandet linjärt. En annan möjlighet är att använda ett annat korrelationsmått som inte gör ett lika starkt antagande gällande variablernas förhållande till varandra. Det är här Spearmans rangkorrelation kommer in.
3.3 Spearmans rangkorrelation
Pearsons korrelationskoefficient mäter styrkan i det linjära sambandet mellan två variabler; Spearmans rangkorrelation mäter styrkan i det monotona sambandet mellan två variabler:
Precis som Pearsons korrelationskoefficient så kan också Spearmans rangkorrelation anta värden mellan -1 och 1. Men Spearmans rangkorrelation antar värdet 1 om det finns ett positivt och strikt monotont förhållande mellan x och y. Det här betyder att y alltid ökar då x ökar (och att x alltid ökar då y ökar). Rangkorrelationen antar värdet -1 om det finns ett negativt och strikt monotont förhållande mellan x och y: y minskar alltid då x ökar och tvärtom. Värdet 0 betyder att det varken finns någon tendens för y att öka eller minska då x ökar.
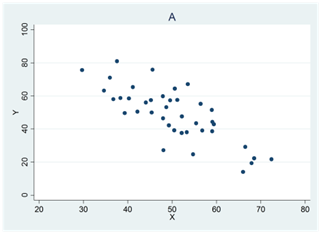
Här är tre exempel på positiva och strikt monotona samband. I alla dessa spridningsdiagram har Spearmans rangkorrelation värdet 1:
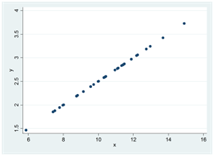
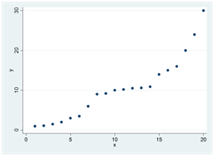
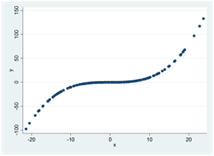
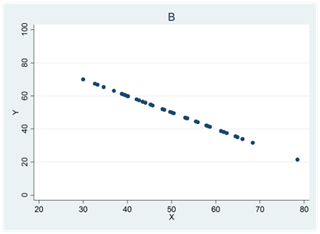
Här är tre exempel på negativa och strikt monotona samband. I alla dessa spridningsdiagram har Spearmans rangkorrelation värdet -1:
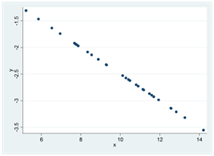
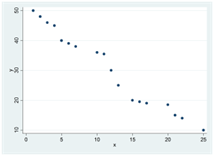
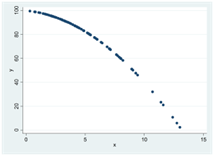
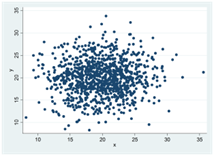
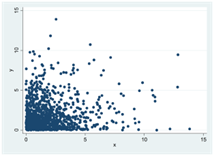
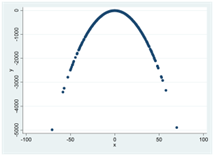
I spridningsdiagrammen nedan har Spearmans rangkorrelation värdet 0 – det finns ingen generell tendens för y att öka eller minska då x ökar:
Hur Spearmans rangkorrelation beräknas
Spearmans rangkorrelation beräknas som Pearsons korrelationskoefficient, bara att vi använder rankingen av variablernas värden istället för rådata.
Exempel. Du vill ta reda på om det finns ett samband mellan avgångsbetyget från högstadiet och framtida lönekrav. För enkelhetens skull tänker vi oss här att samplet enbart består av fem personer:
| Person | Avgångsbetyg | Lönekrav |
|---|---|---|
| 1 | 7,0 | 2 000 |
| 2 | 6,8 | 2 000 |
| 3 | 8,0 | 2 300 |
| 4 | 7,5 | 2 500 |
| 5 | 9,1 | 3 500 |
Vi börjar med att skapa nya variabler som anger rankingen av de gamla variablernas värden. Vi ger personen med det lägsta betyget rankingen 1; personen med det näst lägsta betyget rankingen 2, osv.:
| Person | Betyg | Rang(Betyg) | Lönekrav | Rang(Lönekrav) |
|---|---|---|---|---|
| 1 | 7,0 | 2 | 2 000 | 1 ⇒ 1,5 |
| 2 | 6,8 | 1 | 2 000 | 2 ⇒ 1,5 |
| 3 | 8,0 | 4 | 2 300 | 3 |
| 4 | 7,5 | 3 | 2 500 | 4 |
| 5 | 9,1 | 5 | 3 500 | 5 |
Det är inte lika självklart hur man rankar lönekraven eftersom två personer har samma lönekrav, dvs. 2000 euro. Vi använder då något som kallas för medelrangmetoden: Personerna med lönekraven på 2000 euro har plats nummer 1 och 2 och får då båda rankingen 1,5, dvs. snittet av 1 och 2. (Och om tre personer hade haft detta lönekrav så hade de alla tre fått rankingen 2, dvs. (1+2+3)/3.)
Vi kan nu beräkna korrelationen mellan Rang(Betyg) och Rang(Lönekrav) på samma sätt som tidigare. Detta ger ett värde på 0,87 vilket representerar en stark positiv korrelation.
Pearson vs Spearman
För typiska spridningsdiagram så antar Pearsons och Spearmans korrelationskoefficienter mer eller mindre samma värde:
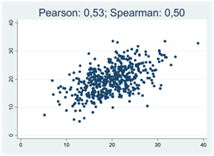
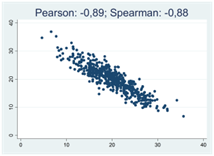
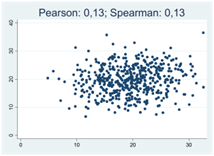
Så när skiljer sig dessa mått från varandra och hur kompletterar de varandra? Det finns tre tillfällen då skillnaderna blir extra tydliga:
- Spearmans rangkorrelation blir generellt sett högre då sambandet beskrivs bättre av en kurva än av en linje.
Figuren nedan visar sambandet mellan inkomst och livslängd i världens länder. Pearsons korrelationskoefficient har här värdet 0,62; Spearmans rangkorrelation har värdet 0,83.
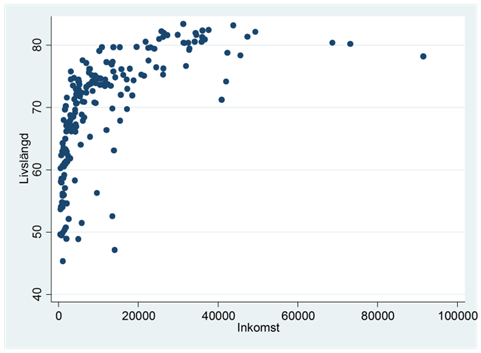
- Spearmans rangkorrelation är inte lika känslig inför avvikande observationer, så kallade outliers.
I små sampel så kan en eller ett par avvikande observationer ha stort inflytande på Pearsons korrelationskoefficient. Figurerna nedan illustrerar detta.
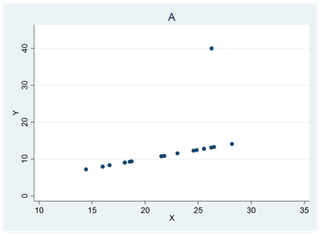
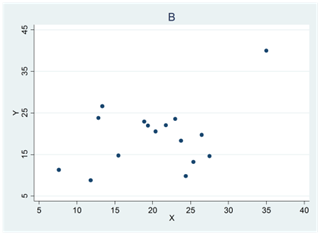
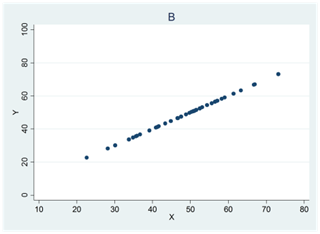
Diagram A visar ett datamaterial där korrelationen skulle ha varit perfekt om det inte vore för den ena avvikande observationen. Men denna har stort inflytande på Pearsons korrelationskoefficient som här har värdet 0,52; Spearmans rangkorrelation påverkas inte i lika hög grad utan har värdet 0,99.
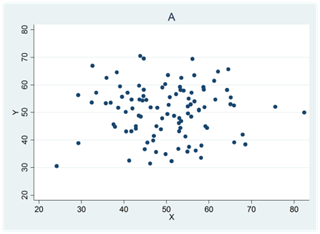
Diagram B visar ett datamaterial där korrelationen hade varit 0 om det inte vore för den ena avvikande observationen. Denna har stort inflytande på Pearsons korrelationskoefficient som här får värdet 0,41; Spearmans rangkorrelation påverkas inte lika mycket utan har värdet 0,06.
- Pearsons korrelationskoefficient lämpar sig för kvantitativa data. Spearmans rangkorrelation lämpar sig dessutom för data på ordinalnivå.
Exempel. Figuren nedan illustrerar sambandet mellan utbildningsnivå och lön. Utbildningsnivå är en variabel med data på ordinalnivå, dvs. en kvalitativ variabel där kategorierna kan rankas på ett meningsfullt sätt.
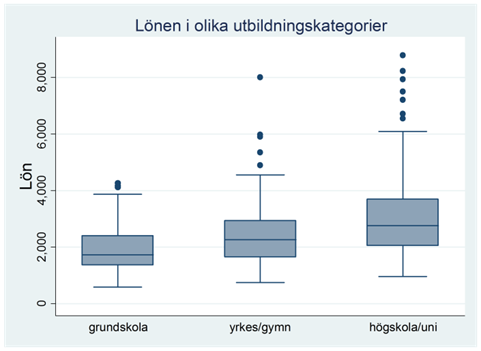
I det här fallet är det högst tveksamt att använda Pearsons korrelationskoefficient. Det finns inget entydigt sätt att koda utbildningskategorierna. Vi kunde exempelvis använda värdena 1, 2 och 3, eller kanske värdena 9, 12 och 17 (vilket ungefär motsvarar hur många år dessa utbildningar tagit). Pearsons korrelationskoefficient skulle här anta olika värden beroende på valet av kodning – och valet är godtyckligt. Det är helt enkelt inte meningsfullt att tala om ett linjärt samband mellan utbildningskategori och lön. Detta är ofta fallet då vi har data på ordinalnivå, dvs. det är då tveksamt att använda Pearsons korrelationskoefficient. Men Spearmans rangkorrelation utnyttjar som sagt bara rangordningen av variablernas värden och då spelar kodningen ingen roll så länge kodningen speglar kategoriernas rangordning. I detta exempel har Spearmans rangkorrelation värdet 0,35.
I det här avsnittet har vi lärt oss om Spearmans rangkorrelation som är det mest använda korrelationsmåttet för data på ordinalnivå. Ett annat liknande mått som också lämpar sig för data på ordinalnivå är Kendalls tau. Läs mer om detta korrelationsmått i Appendix.
Sammanfattning
Appendix
Kendalls tau
Kendalls tau är ett korrelationsmått som också bygger på rankingen av observationernas värden. Det har därför en del likheter med Spearmans rangkorrelation. Precis som Pearsons och Spearmans korrelationskoefficienter så kan också Kendalls tau anta värden mellan -1 och 1.
Vi beräknar Kendalls tau (rk) som:
\[r_{k} = \frac{antalet\ samstämda\ par - antalet\ osamstämda\ par}{totala\ antalet\ par}\]
Exempel. Två domare, Kalle och Anna, bedömer fem stycken danspar i Let’s Dance. Resultatet:
| Danspar | Poäng enligt Kalle | Poäng enligt Anna |
|---|---|---|
| 1 | 10 | 9 |
| 2 | 4 | 2 |
| 3 | 5 | 4 |
| 4 | 8 | 7 |
| 5 | 9 | 10 |
Är domarna samstämda eller inte? Vi säger att domarna är samstämda om, säg, båda tycker att danspar #1 är bättre än danspar #2. Vi säger att domarna är osamstämda om den ena tycker att danspar #1 är bättre än #5, medan den andra tycker tvärtom. På det här viset jämför vi Kalles och Annas poängsättning för varje kombination av danspar:
| Jämförelse av danspar | Samstämda | Osamstämda |
|---|---|---|
| 1 & 2 | x | |
| 1 & 3 | x | |
| 1 & 4 | x | |
| 1 & 5 | x | |
| 2 & 3 | x | |
| 2 & 4 | x | |
| 2 & 5 | x | |
| 3 & 4 | x | |
| 3 & 5 | x | |
| 4 & 5 | x | |
| Σ = 9 | Σ = 1 |
Vi kan nu räkna ut att Kendalls tau har värdet 0,8:
\[r_{k} = \frac{antalet\ samstämda\ par - antalet\ osamstämda\ par}{totala\ antalet\ par} = \frac{9 - 1}{10} = 0,8\]
Kendalls tau har en tydlig tolkning – den är en skillnad mellan två sannolikheter – sannolikheten för att Anna och Kalle ska tycka lika minus sannolikheten för att Anna och Kalle ska tycka olika. Om vi slumpmässigt väljer ut två danspar så är sannolikheten för att Anna och Kalle tycker lika 80 procentenheter högre än sannolikheten att de tycker olika.
Analysen blir lite mer komplicerad om Anna (eller Kalle) gett lika många poäng till två eller flera danspar. Det finns olika sätt att behandla sådana situationer, men vi går inte in på detaljerna här.
Övningsuppgifter
Samband
- Det finns en hypotes om att födelsemånaden spelar roll för hur bra du klarar dig i skolan: Ju tidigare på året du är född, desto bättre. Du vill nu testa om det ligger någon sanning i den här hypotesen och samlar in data om ett tusental elever i årskurs nio, deras födelsemånad (variabeln månad som antar värden mellan 1 och 12, där 1 = Januari, 2 = Februari, …, 12 = December) och betyg (variabeln betyg). Anta att hypotesen ovan är korrekt. Hur ser då sambandet mellan variablerna månad och betyg ut (positiv, negativ eller inget samband)? Förklara.
Pearsons korrelationskoefficient
- Vilket eller vilka av följande påståenden är korrekta:
En korrelation på 0,6 betyder att sambandet är starkare än om korrelationen är -0,6.
Det är inte möjligt att få en korrelation på 1,4.
Om sambandet mellan två variabler beskrivs av en kurva (se nedan) så har Pearsons korrelationskoefficient värdet 0.
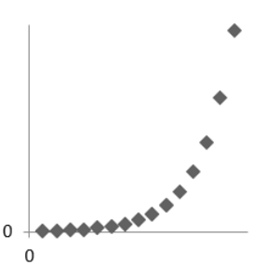
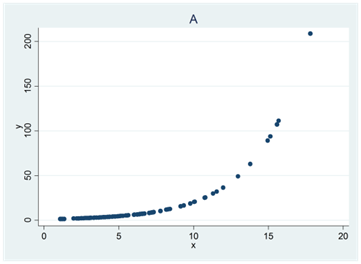
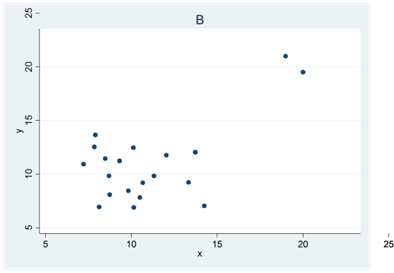
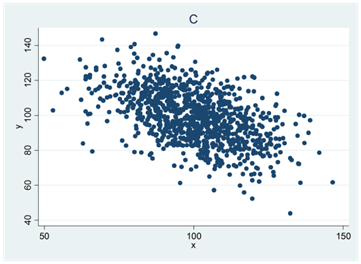
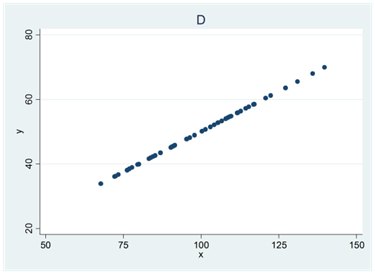
- Se spridningsdiagrammen nedan (A, B, C och D). I ett diagram är korrelationen 0,4; i ett annat 0; i ett tredje -0,5 och i ett fjärde 0,7. Para ihop rätt korrelationskoefficient med rätt spridningsdiagram.
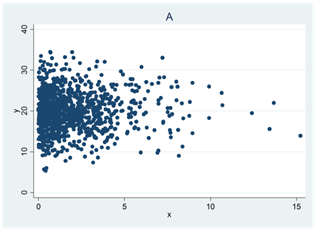
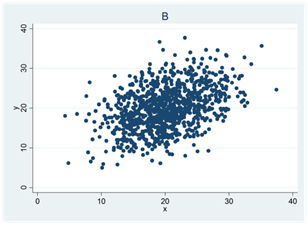
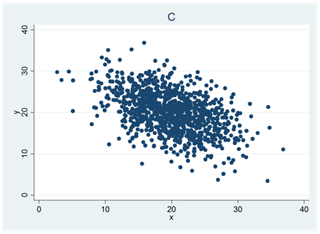
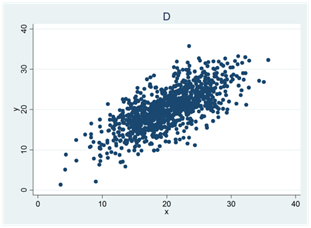
- Tabellen nedan visar arbetserfarenhet och lön för åtta personer. Arbetserfarenheten mäts i antal år och lönen i euro per månad. Den genomsnittliga arbetserfarenheten är 5 år; den genomsnittliga lönen är 2720 euro; variansen för arbetserfarenheten är 30,6 och lönevariansen är 792 486.
| id | Arbetserfarenhet | Lön |
|---|---|---|
| 1 | 0 | 3100 |
| 2 | 1 | 2000 |
| 3 | 1 | 2500 |
| 4 | 2 | 1750 |
| 5 | 4 | 3000 |
| 6 | 6 | 2200 |
| 7 | 10 | 2610 |
| 8 | 16 | 4600 |
Beräkna korrelationen mellan arbetserfarenhet och lön.
Hur stor hade korrelationen blivit om lönen istället mättes i tusentals euro?
- I tabellen nedan visas data för tre variabler: kön, x och y.
| id | kön | x | y |
|---|---|---|---|
| 1 | Man | 0 | 5 |
| 2 | Man | 1 | 4 |
| 3 | Man | 1 | 7 |
| 4 | Man | 2 | 6 |
| 5 | Man | 2 | 8 |
| 6 | Kvinna | 3 | 0 |
| 7 | Kvinna | 3 | 2 |
| 8 | Kvinna | 4 | 2 |
| 9 | Kvinna | 4 | 4 |
| 10 | Kvinna | 5 | 3 |
Beräkna korrelationen mellan x och y för männen. Bland männen är kovariansen mellan variablerna 0,75; variansen för x är 0,7 och variansen för y är 2,5.
Beräkna korrelationen mellan x och y för kvinnorna. Bland kvinnorna är kovariansen mellan variablerna 0,8; variansen för x är 0,7 och variansen för y är 2,2.
Beräkna nu korrelationen mellan x och y i hela samplet. I hela samplet är kovariansen mellan variablerna är -2,056; variansen för x är 2,5 och variansen för y är 6,1.
Jämför svaren på a-c: Det här fenomenet kallas för Simpson’s paradox. Paradoxen består i att korrelationen för både männen och kvinnorna är positiv, medan korrelationen för hela samplet är negativ. Hur kan det komma sig? För att se lösningen – rita upp observationerna i ett spridningsdiagram:

- Ett bra sätt att lära sig om vad logaritmering gör är att visualisera. Här ser du sambandet mellan BNP per capita och barnadödlighet. Ändra skalan för en axel via settings. Här ser du sambandet mellan BNP per capita och koldioxidutsläpp per capita. Testa dig fram – vilken skala passar data bäst?
Spearmans rangkorrelation
- Hitta på ett datamaterial som består av åtta observationer, och där …
Spearmans rangkorrelation har ett positivt värde.
Spearmans rangkorrelation har värdet -1, medan Pearsons korrelationskoefficient inte har det.
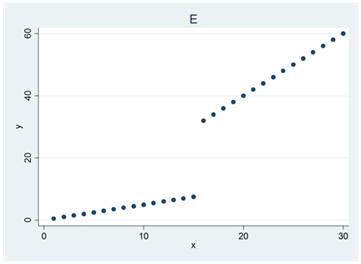
- Se spridningsdiagrammen nedan (A, B, C, D och E).
I tre av diagrammen har Spearmans rangkorrelation värdet 1. Vilka tre?
I två av diagrammen är Spearmans rangkorrelation större än Pearsons. Vilka två?
I två av diagrammen är Spearmans och Pearsons korrelationskoefficienter lika stora. Vilka två?
I ett av diagrammen är Pearsons korrelationskoefficient större än Spearmans. Vilket?
- Nedan ser du en tabell klippt ur artikeln Income inequality, perceived happiness, and self-rated health: Evidence from nationwide surveys in Japan. Här har författarna bland annat mätt sambandet mellan hälsa och lycka med Spearmans rangkorrelation. Data täcker tiotusentals japaner.
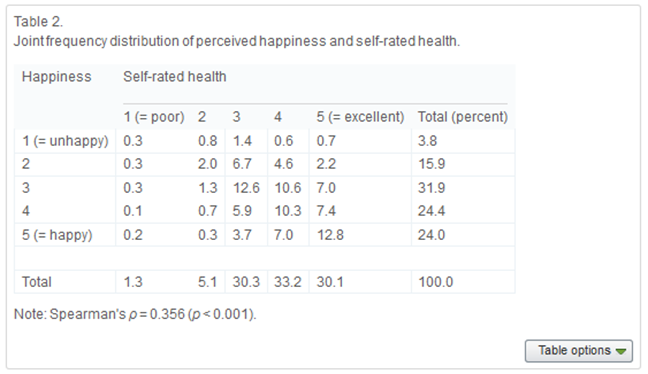
- I det här fallet är det lämpligare att använda Spearmans rangkorrelation än Pearsons. Förklara kortfattat varför.
- Nämn ett annat korrelationsmått som också kunde användas i detta fall.