| Tvärsnittsdata | ||
|---|---|---|
| Land | Inkomst | Livslängd |
| Afghanistan | 1 907 | 56,2 |
| Albanien | 9 489 | 75,8 |
| Algeriet | 12 957 | 76,3 |
| Angola | 7 319 | 60,4 |
| … | … | … |
| Zimbabwe | 1 445 | 56,0 |
7 Att beskriva tidsseriedata
De sampel vi sett på hittills har varit exempel på tvärsnittsdata. Det betyder att vi samlat in data för alla individer (eller hushåll/företag/länder …) vid en viss tidpunkt. Om vi mäter inkomst per person i 200 länder år 2014 så är det ett exempel på tvärsnittsdata.
För att lära sig om hur saker utvecklas över tid använder vi istället tidsseriedata. Vi har en tidsserie då vi gör upprepade mätningar för en och samma individ (eller hushåll/företag/land/…) över flera tidsperioder. Exempel: Vi mäter inkomst per person i Finland mellan åren 1800 och 2013. Tabellerna nedan visar hur skillnaden mellan tvärsnittsdata och tidsseriedata ser ut då data sammanställts i en datamatris. Tvärsnittsdata gäller olika länder år 2013; tidsserien gäller Finland mellan åren 1800-2013.
| Tidsseriedata | ||
|---|---|---|
| År | Inkomst | Livslängd |
| 1800 | 1 261 | 36,6 |
| 1801 | 1 263 | 40,3 |
| 1802 | 1 266 | 39,2 |
| 1803 | 1 268 | 28,5 |
| … | … | … |
| 2013 | 37 341 | 80,6 |
I det här kapitlet ska vi fundera över hur man beskriver tidsseriedata. Allt som vi lärt oss hittills om hur man beskriver sampel genom beskrivande mått såsom medelvärden, standardavvikelser, korrelationer och regressioner gäller också för tidsserier. Men för att illustrera tidsserier använder vi oftast tidsseriediagram. Vi ska börja med att se några exempel på sådana.
12. Att beskriva tidsseriedata, del 1
13. Att beskriva tidsseriedata, del 2
7.1 Tidsseriediagram och utjämning
Tidsseriediagram illustrerar en variabels utveckling över tiden. Här ges några exempel:
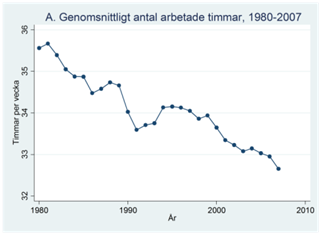
Exempel. Arbetslösheten har sjunkit nästan varje år sedan krisen på 90-talet. Trots detta jobbar finländare hela tiden allt mindre. Figuren nedan visar antalet arbetade timmar under en vecka för en genomsnittlig finländare under åren 1980-2007.
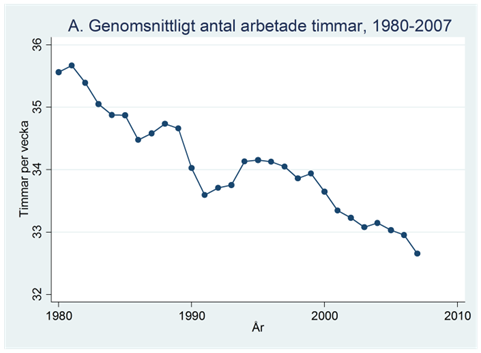
Exempel. Figuren nedan illustrerar det som kallas för Moores lag: att antalet transistorer i mikroprocessorer ökat med en exponentiell takt över tiden.
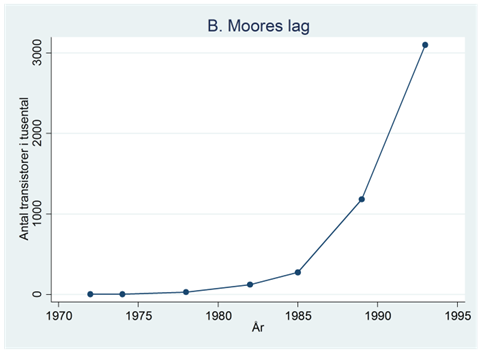
Exempel. Nedan visas genomsnittlig BMI bland amerikanska kvinnor mellan åren 1980 och 2008. BMI mäter relationen mellan vikt och längd; högre värden innebär att man väger mer relativt sin längd.
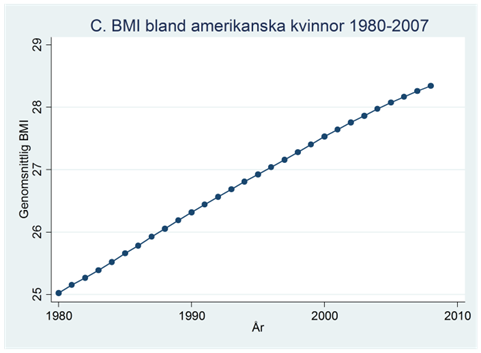
Exempel. Figuren nedan visar procenten deltidsanställda män bland alla finländska manliga löntagare under åren 1997-2014. Data visas per kvartal, där första och tredje kvartalen märkts ut skilt.
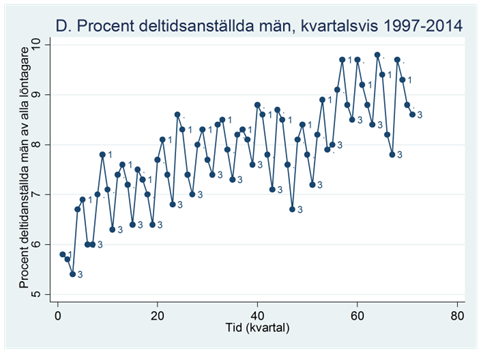
När vi illustrerar en variabels utveckling över tid är syftet ofta att beskriva den generella trenden i data. För att göra det mönstret synligare så kan vi börja med att jämna ut serien, dvs. rensa den på kortsiktiga fluktuationer så att den långsiktiga trenden blir tydlig. Ett populärt sätt att åstadkomma detta är genom glidande medelvärden.
Centrerat glidande medelvärde
Vi ser bäst vad glidande medelvärden gör genom ett exempel:
Exempel. Figuren nedan visas hur mycket en genomsnittlig finländare jobbade per vecka under åren 1980-2007.
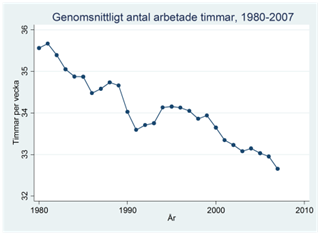
År 2000 jobbade den genomsnittliga finländaren 33,6 timmar per vecka. Året innan (1999) var denna siffra 33,9 timmar och året efter (2001) 33,3 timmar. Medelvärdet över de här tre åren är 33,6 timmar, dvs. (33,6+33,9+33,3)/3 = 33,6. Vi kallar detta för ett centrerat glidande medelvärde för år 2000: Vi har beräknat medelvärdet genom att använda tre år centrerade kring år 2000.
I tabellen nedan har vi beräknat ett centrerat glidande medelvärde (CGM) för varje år i tidsserien, förutom det första och sista året. Det första året (1980) faller bort eftersom vi inte har data för år 1979 och det sista året (2007) eftersom vi inte har data för år 2008.
| År | Arbetstimmar | CGM |
|---|---|---|
| 1980 | 35,60 | – |
| 1981 | 35,70 | 35,57 |
| 1982 | 35,40 | 35,40 |
| 1983 | 35,10 | 35,13 |
| 1984 | 34,90 | 34,93 |
| … | … | … |
| 2005 | 33,00 | 33,04 |
| 2006 | 33,00 | 32,90 |
| 2007 | 32,70 | – |
I det här exemplet använde vi tre år för att beräkna det glidande medelvärdet. Men vi kan också använda fler, t.ex. fem. Tabellen nedan visar att det centrerade glidande medelvärdet för år 1982 då blir 35,34 timmar; detta är snittet beräknat över de fem åren 1980-1984 där 1982 ligger mitterst. Notera nu att vi förlorar två värden i början och slutet av serien.
| År | Arbetstimmar | CGM |
|---|---|---|
| 1980 | 35,6 | – |
| 1981 | 35,7 | – |
| 1982 | 35,4 | 35,34 |
| 1983 | 35,1 | 35,17 |
| 1984 | 34,9 | 34,93 |
| … | … | … |
| 2005 | 33,0 | 32,97 |
| 2006 | 33,0 | – |
| 2007 | 32,7 | – |
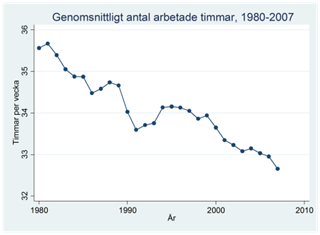
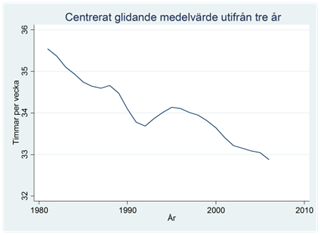
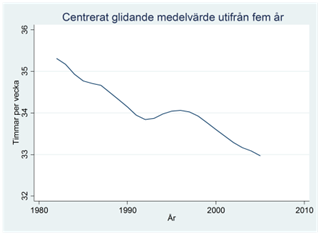
Syftet med att beräkna glidande medelvärden är att få en utjämnad serie som inte innehåller lika mycket variation kring den långsiktiga trenden, dvs. vi vill göra den långsiktiga trenden tydlig. I figurerna nedan visas originaldata, samt serierna med glidande medelvärden beräknade utifrån tre och fem år.
Exempel. Nedan visas procenten deltidsanställda män bland alla manliga löntagare under åren 1997-2014. Data är på kvartalsnivå. Vi kan se att de deltidsanställda ökat över tiden, men om vi kunde jämna ut säsongsvariationen så skulle detta bli ännu tydligare. Vi ska nu se hur vi kan använda centrerade glidande medelvärden i detta syfte.
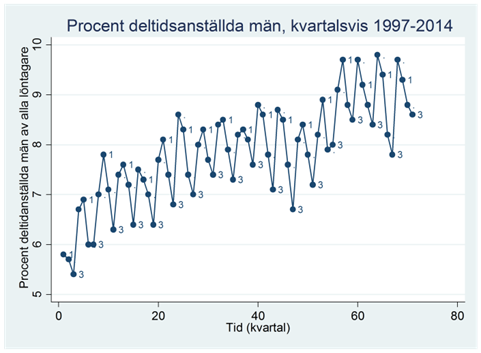
Tabellen nedan visar de första två åren av den här tidsserien. I den fjärde kolumnen har vi räknat ut det centrerade glidande medelvärdet utifrån fem kvartal. För det tredje kvartalet år 1997 så blir det glidande medelvärdet 6,1 procent.
| År | Kvartal | Procent deltidsanställda |
CGM, 5 kvartal |
|---|---|---|---|
| 1997 | 1 | 5,8 | – |
| 1997 | 2 | 5,7 | – |
| 1997 | 3 | 5,4 | 6,10 |
| 1997 | 4 | 6,7 | 6,14 |
| 1998 | 1 | 6,9 | 6,20 |
| 1998 | 2 | 6,0 | 6,52 |
| 1998 | 3 | 6,0 | 6,74 |
| 1998 | 4 | 7,0 | 6,78 |
| … | … | … | … |
Detta medelvärde (6,1) är delvis säsongsutjämnat eftersom det är en sammanvägning av värden från alla fyra kvartal. Men det första kvartalet har fått dubbelt större inflytande än något av de andra kvartalen; det första kvartalet tas ju med två gånger. Vi kan lösa detta genom att ge dessa två värden hälften så mycket vikt:
\[CGM = \frac{{\color{red}{0,5 \times 5,8}} + 5,7 + 5,4 + 6,7 + {\color{red}{0,5 \times 6,9}}}{4} = 6,0375\]
Notera att vi nu delar med fyra och inte fem, eftersom två av observationerna bara räknas hälften så mycket; det är som om vi bara hade använt fyra observationer. Vi säger att det här är ett centrerat glidande medelvärde utifrån fyra kvartal.
Tabellen nedan visar detta glidande medelvärde för de första två åren:
| År | Kvartal | Procent deltidsanställda |
CGM, 4 kvartal |
|---|---|---|---|
| 1997 | 1 | 5,8 | — |
| 1997 | 2 | 5,7 | — |
| 1997 | 3 | 5,4 | 6,0375 |
| 1997 | 4 | 6,7 | 6,2125 |
| 1998 | 1 | 6,9 | 6,3250 |
| 1998 | 2 | 6,0 | 6,4375 |
| 1998 | 3 | 6,0 | 6,5875 |
| 1998 | 4 | 7,0 | 6,8375 |
| — | — | — | — |
Till vänster visas rådata; till höger den säsongsutjämnade serien:
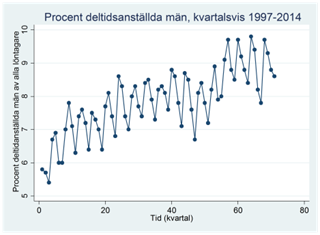
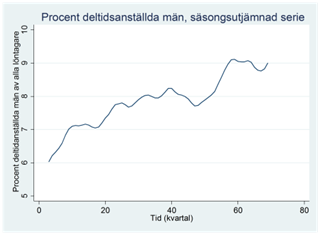
Säsongsvariation uppstår ofta i serier där man mäter något flera gånger om året såsom kvartalsvis eller månadsvis. Anta exempelvis att vi vill göra en säsongsutjämning utifrån månadsdata, och att vi ska beräkna det glidande medelvärdet för augusti månad ett visst år:
Feb, Mars, April, Maj, Juni, Juli, Aug, Sep, Okt, Nov, Dec, Jan, Feb
Vi vill då beräkna medelvärdet utifrån alla tolv månader så att alla får samma inflytande i det glidande medelvärdet. I det här fallet använder vi då alla värden mellan februari-februari, men ger värdena för februari månad hälften av vikten.
Vad använder vi tidsserier till?
I det här avsnittet har vi sett hur man kan illustrera en tidsserie. Vi ska nu gå över till att se hur vi kan analysera tidsseriedata. Men för att göra detta så måste vi först fundera på vilken typ av frågor det är vi vill besvara. Generellt kunde man dela frågeställningarna i tre typer:
1) Beskriva den historiska utvecklingen i en tidsserie. Exempel: Har klyftorna mellan rika och fattiga i Finland minskat eller ökat över tid?
2) Prognostisering; vi använder historiska mönster för att förutspå framtiden. Exempel: Vi använder historiska data över bostadspriser för att göra prognoser för framtida priser.
3) Förklara hur den historiska utvecklingen påverkats av andra faktorer. Exempel: Kan reklamutgifterna förklara variationen i försäljningssiffror över tid?
Oavsett om man vill beskriva en historisk utveckling eller göra prognoser så är utgångspunkten densamma; vi börjar med att beskriva mönstret i tidsserien. I nästa avsnitt (7.2) ska vi se hur vi kan beskriva olika sorters trender i data.
7.2 Att beskriva trender över tid
När vi talar om trender så menar vi att medelvärdet för serien varierar systematiskt över tid. I det här kapitlet ska vi fundera över hur vi kan beskriva ett sådant mönster i data. Nedan visas tidsserierna från föregående avsnitt:
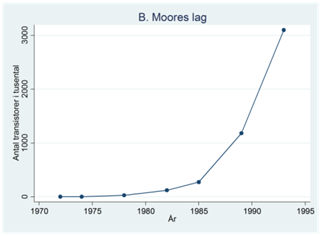
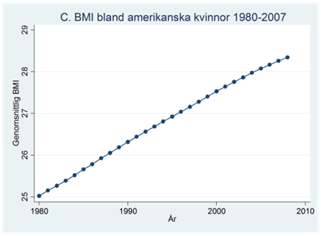
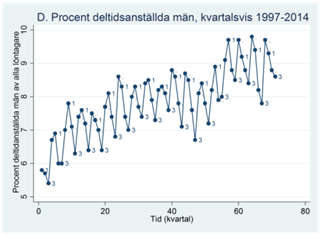
Hur kan vi karaktärisera dessa tidsserier? Vi kan tänka på tidsserien som uppbyggd av två komponenter: En deterministisk komponent och därutöver slumpmässiga fluktuationer. Den deterministiska komponenten är det regelbundna mönstret i tidsserien. I figur A ser vi en nedåtgående trend över tiden; i figur B ser vi en tilltagande ökning över tiden; figur C har en uppåtgående trend men den verkar avta lite mot slutet; figur D har en uppåtgående trend men också tydlig säsongsvariation, dvs. andelen deltidsanställda varierar systematiskt beroende på kvartal.
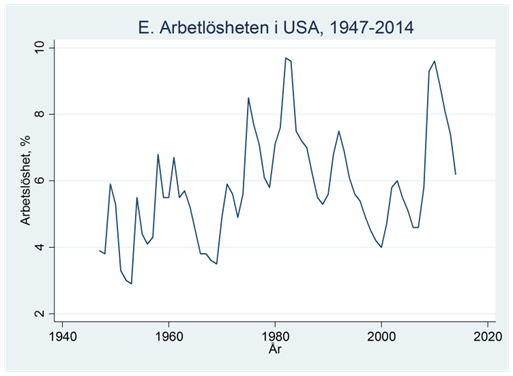
Förutom säsongsvariation så finns det också tidsserier som karaktäriseras av cyklisk variation. Figur E nedan är ett exempel på detta. Här ser vi arbetslösheten i USA mellan åren 1947 och 2014. Arbetslösheten har periodvis gått upp och periodvis ner, men till skillnad från säsongsvariation så är dessa växlingar inte knutna till regelbundna säsonger.
Linjär trend
Exempel. Figuren nedan visas hur mycket en genomsnittlig finländare jobbade per vecka under åren 1980-2007.
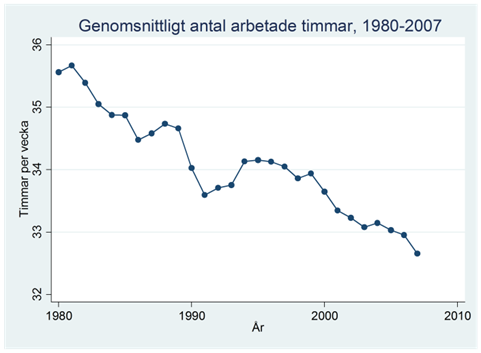
Vi ser att en linjär trend skulle kunna passa som en beskrivning av utvecklingen över tid, men hur kan vi mäta en sådan trend? Jo, vi kan använda regressionslinjen där vi låter tiden vara oberoende variabel:
\[\widehat{arbetstimmar} = a + b \times tid\]
Här visas ett utdrag av data:
| År | Tid | Arbetstimmar |
|---|---|---|
| 1980 | 0 | 35,6 |
| 1981 | 1 | 35,7 |
| 1982 | 2 | 35,4 |
| 1983 | 3 | 35,1 |
| … | … | … |
| 2007 | 27 | 32,7 |
Som du ser så har vi här skapat en variabel, tid, som antar värdet 0 det första året i data (1980); värdet 1 det andra året i data (1981); värdet 2 året därpå, osv. Vi kör nu en regression med antalet arbetstimmar som utfall och tid som oberoende variabel:
\[\widehat{arbetstimmar} = 35,35 - 0,094 \times tid\]
Vi kan använda den här regressionen för att göra prediktioner. År 1980 (tid = 0) predikteras arbetsveckan vara 35,35 timmar lång:
\[\widehat{arbetstimmar} = 35,35 - 0,094 \times \underbrace{tid}_{=0} = 35,35\]
27 år senare (tid = 27) predikteras arbetsveckan vara ~32,8 timmar:
\[\widehat{arbetstimmar} = 35,35 - 0,094 \times \underbrace{tid}_{=27} \approx 32,8\]
Vi kan också använda regressionen för att sia om framtiden. År 2015 (tid = 35) prognostiseras man jobba 32,06 timmar per vecka:
\[\widehat{arbetstimmar} = 35,35 - 0,094 \times \underbrace{tid}_{=35} = 32,06\]
Kan man lita på den här prognosen? Den här prognosen bygger på antagandet om att trenden kommer att fortsätta som tidigare, och detta är nog inte alltid trovärdigt, i synnerhet om vi vill blicka långt in i framtiden.
I det här exemplet använde vi variabeln tid som oberoende variabel, men vi kunde lika bra ha använt variabeln år och fått exakt samma prediktioner. Men genom att använda variabeln tid som startar från noll så får interceptet också en naturlig betydelse; interceptet (35,35) visar då prediktionen för det första året i data (1980).
I diagrammet nedan har vi ritat in regressionslinjen i rött. Den visar att arbetstiden i snitt minskat med 0,094 timmar (~6 minuter) per år. Grovt räknat så har arbetstiden minskar med cirka en timme per decennium.
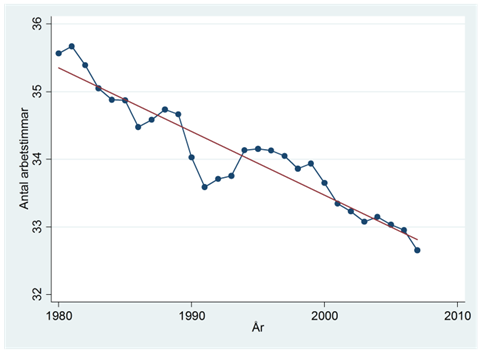
Exponentiell trend
Tidigare har vi sett att man ibland kan logaritmera y- eller x-variabeln för att få en regressionslinje som bättre passar data. Det går också bra att logga y-variabeln då vi har att göra med tidsseriedata. Figuren nedan visar utvecklingen i Finlands loggade befolkningsmängd mellan åren 1870 och 1900. I rött visas regressionslinjen:
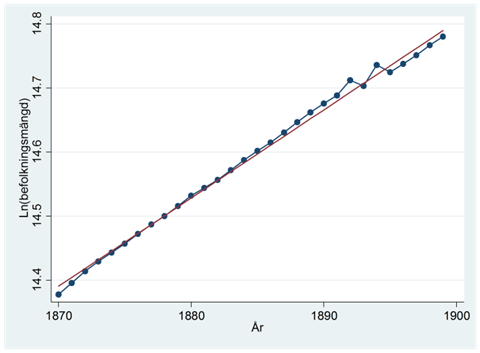
Regressionslinjen ges av:
\[\widehat{ln(befolkningsmängd)} = - 11,37 + 0,014 \times år\]
Regressionslinjen visar att befolkningsmängden stigit med ungefär 1,4 procent årligen under den här perioden. När en variabel på det här viset ökar med en viss procent årligen så kallar vi det för expontiell tillväxt.
Kvadratisk trend
Exempel. Diagrammet nedan visar utvecklingen i BMI bland amerikanska kvinnor. I rött visas regressionslinjen:
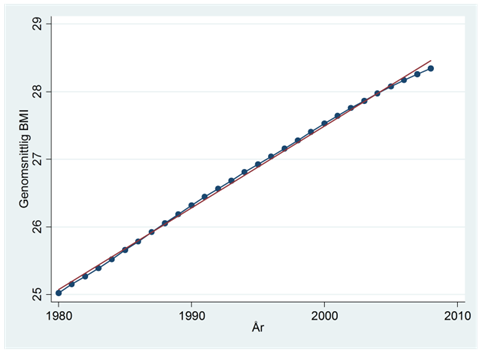
Som du ser så överskattar regressionslinjen BMI under de första åren; underskattar BMI i mitten av perioden och överskattar BMI under de sista åren. Skillnaden mellan den linjära trenden och den verkliga utvecklingen är hårfin, men systematisk. Det här betyder att vi kan hitta ett bättre sätt att beskriva utvecklingen över tid. I det här exemplet skulle en kvadratisk trend passa bra. Så vad menas med en kvadratisk trend?
För att se vad en kvadratisk trend betyder så ska vi börja med att jämföra med en linjär trend. Figuren nedan beskriver en positiv linjär trend; ökningen mellan tidpunkt 0 och 1 är lika stor som ökningen mellan tidpunkt 5 och 6 eller som den mellan tidpunkt 9 och 10; för varje period så ökar y med en enhet.
| Tid | Y | ökning |
|---|---|---|
| 0 | 0 | … |
| 1 | 1 | +1 |
| 2 | 2 | +1 |
| 3 | 3 | +1 |
| … | … | … |
| 9 | 9 | +1 |
| 10 | 10 | +1 |
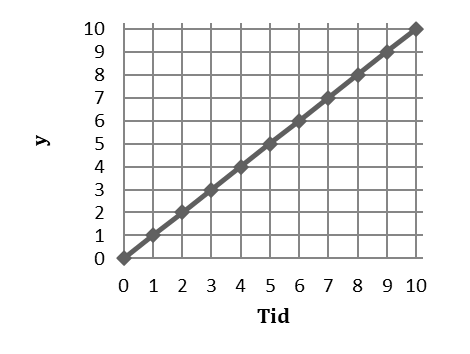
Men låt oss nu anta att ökningen är positiv men avtagande. Se tabellen nedan. Mellan tidpunkt 0 och 1 så ökar y med 1 enhet; därefter är ökningen 0,9 enheter, därefter 0,8 enheter, därefter 0,7 enheter, osv. Detta är ett exempel på en kvadratisk trend; ökningen minskar med 0,1 enheter för varje period.
| Tid | y | ökning |
|---|---|---|
| 0 | 0,0 | |
| 1 | 1,0 | +1 |
| 2 | 1,9 | +0,9 |
| 3 | 2,7 | +0,8 |
| 4 | 3,4 | +0,7 |
| 5 | 4,0 | +0,6 |
| 6 | 4,5 | +0,5 |
| 7 | 4,9 | +0,4 |
| 8 | 5,2 | +0,3 |
| 9 | 5,4 | +0,2 |
| 10 | 5,5 | +0,1 |
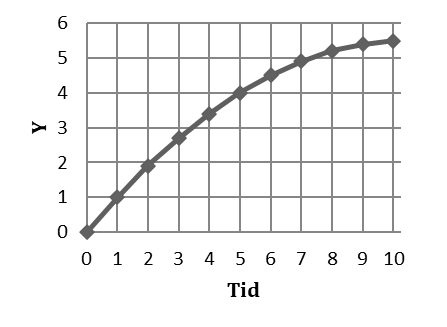
Vi beskriver den här utvecklingen genom en kvadratisk ekvation:
\[\widehat{y} = 0 + {\color{red}{1,05}}tid {\color{blue}{-1,05}}{tid}^{2}\]
Den här ekvationen visar två saker: 1) Exakt vid tidpunkt 0 så ökar y med 1,05 enheter. 2) Ökningen i y minskar med \(2 \times \textcolor{blue}{0,05} = 0,1\) enheter för varje period.
Här är ett annat exempel på en kvadratisk trend men här är ökningen i y tilltagande; mellan tidpunkt 0 och 1 så ökar y med 1 enhet, därefter är ökningen 1,2 enheter, därefter 1,4 enheter, därefter 1,6 enheter, osv. Ökningen ökar med 0,2 enheter för varje period.
| Tid | y | ökning |
|---|---|---|
| 0 | 2,0 | |
| 1 | 3,0 | +1 |
| 2 | 4,2 | +1,2 |
| 3 | 5,6 | +1,4 |
| 4 | 7,2 | +1,6 |
| 5 | 9,0 | +1,8 |
| 6 | 11,0 | +2,0 |
| 7 | 13,2 | +2,2 |
| 8 | 15,6 | +2,4 |
| 9 | 18,2 | +2,6 |
| 10 | 21,0 | +2,8 |
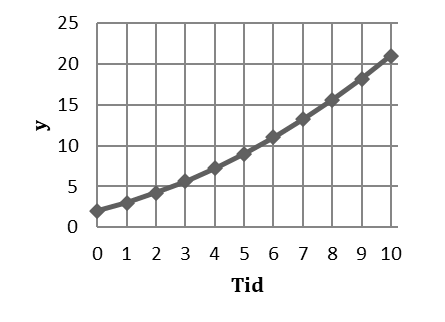
Vi beskriver den här trenden genom ekvationen:
\[\widehat{y} = 2 + 0,9tid + 0,1{tid}^{2}\]
Här är ett exempel där minskningen i y tilltar med 1 enhet per period; mellan tidpunkt 0 och 1 så minskar y med 5 enheter, därefter med 6 enheter, därefter med 7 enheter, osv.
| År | y | förändring |
|---|---|---|
| 0 | 100 | |
| 1 | 95 | -5 |
| 2 | 89 | -6 |
| 3 | 82 | -7 |
| 4 | 74 | -8 |
| 5 | 65 | -9 |
| 6 | 55 | -10 |
| 7 | 44 | -11 |
| 8 | 32 | -12 |
| 9 | 19 | -13 |
| 10 | 5 | -14 |
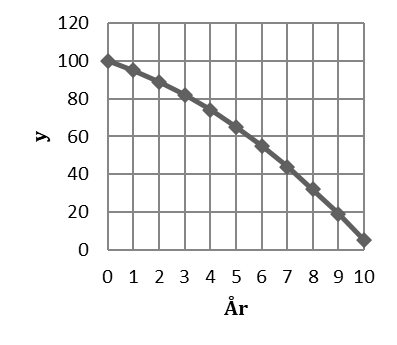
Vi beskriver den här trenden genom ekvationen:
\[\widehat{y} = 100 - 4,5tid - 0,5{tid}^{2}\]
Exempel forts. Diagrammet nedan visar trenden i BMI bland amerikanska kvinnor:
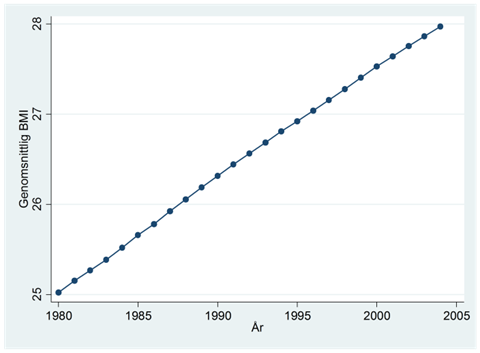
Den här utvecklingen skulle beskrivas bra av en kvadratisk trend, men hur anpassar vi en sådan trend till data i praktiken? Jo, vi gör detta genom att köra en multipel regression där vi både inkluderar tiden och tiden i kvadrat som oberoende variabler.
Här ges ett utdrag av datamaterialet:
| År | Tid | Tid2 | BMI |
|---|---|---|---|
| 1980 | 0 | 0 | 25,02199 |
| 1981 | 1 | 1 | 25,15155 |
| 1982 | 2 | 4 | 25,26646 |
| 1983 | 3 | 9 | 25,38480 |
| 1984 | 4 | 16 | 25,52017 |
| … | … | … | … |
| 2004 | 24 | 576 | 27,97255 |
Som du ser så har vi här skapat en ny variabel som heter tid; den antar värdet 0 det första året i data (1980) och värdet 1 året därpå (1981), osv. Om vi kör en regression som inkluderar både variablerna tid och tid2 så får vi resultatet:
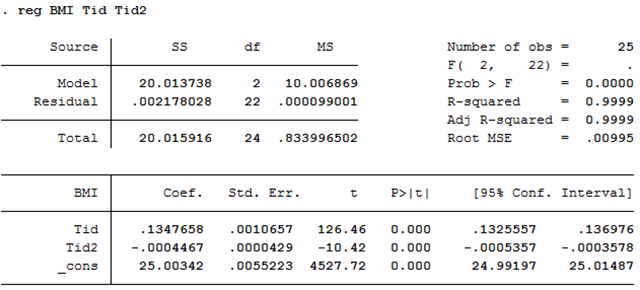
Regressionen:
\[\widehat{bmi} = 25,0 + 0,135tid - 0,000447{tid}^{2}\]
Koefficienten för tid är positiv vilket visar att vi har en positiv trend åtminstone från början av perioden; koefficienten för tid2 är negativ vilket visar att trenden är avtagande.
Precis som tidigare så kan vi använda regressionen för att göra prediktioner. År 1984 (tid = 4) så predikteras amerikanska kvinnor ha ett genomsnittligt BMI på ~25,5:
\[\widehat{bmi} = 25,0 + 0,135\underbrace{tid}_{=4} - 0,000447\underbrace{tid^2}_{=4^2} \approx 25,5\]
Tjugo år senare (tid = 24) så predikteras BMI ha stigit till ~28 enheter:
\[\widehat{bmi} = 25,0 + 0,135\underbrace{tid}_{=24} - 0,000447\underbrace{tid^2}_{=24^2} \approx 28,0\]
Regressionslinjen (eller –kurvan) nedan i rött visar dessa prediktioner för varje år i serien. Som vi ser så sammanfaller regressionslinjen nästan exakt med den verkliga trenden i blått:
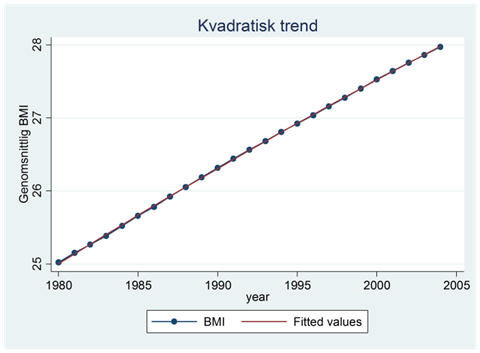
Hur realistisk är den här modellen om vi vill sia långt in i framtiden? Tja, precis som för andra trendmodeller så bygger prognoserna på att trenden håller i sig, vilket sällan är helt realistiskt på längre sikt. Kvadratiska trender har också den egenskapen att de förr eller senare når antingen en toppen eller botten, vilket inte nödvändigtvis passar in så bra på utvecklingen i egentliga data. I BMI-exemplet så prognostiseras vi nå toppen av kurvan år 2131, varefter trenden prognostiseras vända. I detta fall ligger dock toppen så pass långt in i framtiden att den inte har någon praktisk betydelse.
Vi kan hitta kurvans maximi eller minimi genom derivering, eller så kan vi använda följande formel:
\[\min{eller\max{= \ \frac{- b}{2c}}}\]
där b är koefficienten för tiden; c är koefficienten för tiden i kvadrat. I detta exempel:
\[max = \frac{- 0,135}{2 \times ( - 0,000447)} \approx 151\]
Det innebär att vi når max då tiden är 151 vilket kan översättas till år 2131.
Trendbrott
Exempel. Figuren nedan visar procenten amerikaner som välkomnar en ökad invandring [fejkat data]. Vi vill ta reda på om inställningen förändrats i och med 9/11.
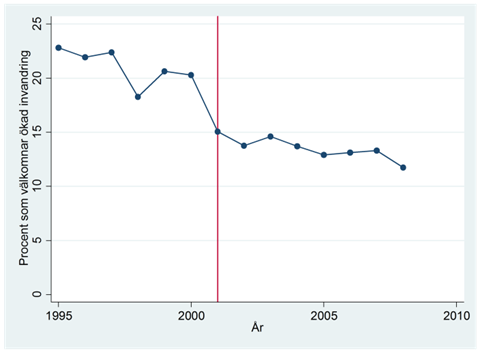
I regressionen nedan är post911 en dummy som antar värdet 1 efter terrordådet och värdet 0 före. Procent mäter procenten som välkomnar en ökad invandring:
\[\widehat{procent} = 21,0 - 7,5post911\]
I snitt har andelen som välkomnar en ökad invandring minskat med 7,5 procentenheter efter 9/11:
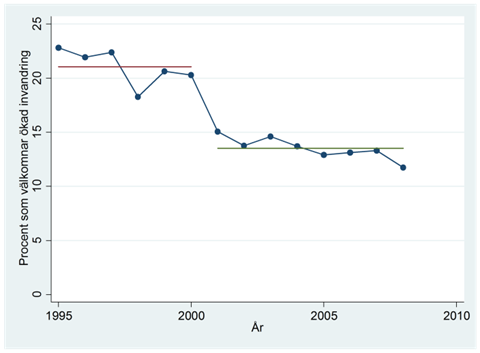
Men vi kan också se att det redan fanns en viss negativ trend före terrordådet. En del av skillnaden kan därför bero på en allmänt kallare attityd till invandring över tiden. Vi kontrollerar därför ännu för den allmänna trenden i tidsserien genom att inkludera variabeln tid:
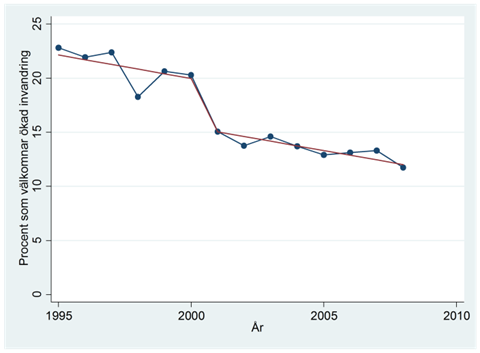
\[\widehat{procent} = 22,1 - 4,5post911 - 0,43 \times tid\]
När vi beaktat den nedåtgående trenden så ser vi fortfarande en negativ effekt av 9/11; andelen som välkomnar en ökad invandring har minskat med 4,5 procentenheter.
Säsongsvariation
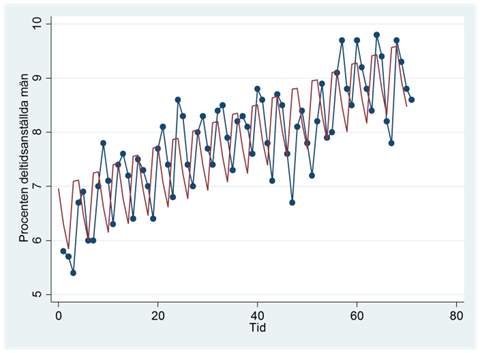
Exempel. Figuren nedan visar procenten deltidsanställda män kvartalsvis mellan åren 1997 och 2014:
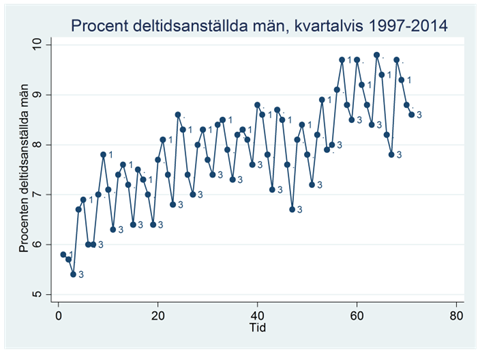
Om vi anpassar en regressionslinje till den här tidsserien så får vi resultatet:
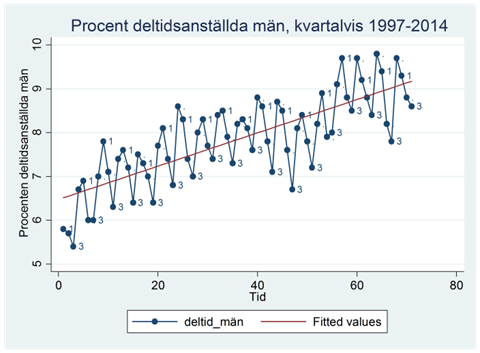
Som du ser så ligger regressionslinjen som regel för lågt i första kvartalet varje år och för högt i tredje kvartalet. Finns det något sätt att beakta att procenten deltidsanställda varierar systematiskt beroende på kvartal?
Låt oss först ignorera den positiva trenden och bara tänka oss följande regression:
\[\widehat{deltid} = a + b_{1}kvartal2 + b_{2}kvartal3 + b_{3}kvartal4\]
där deltid mäter procenten deltidsanställda män. Kvartal2 är en dummy som antar värdet 1 detta kvartal och värdet 0 alla andra kvartal; kvartal3 och kvartal4 är på motsvarande sätt dummyn för det tredje och fjärde kvartalet.
Nedan visas ett utdrag av data:
| År-kvartal | Tid | Kvartal2 | Kvartal3 | Kvartal4 | deltid |
|---|---|---|---|---|---|
| 1997-1 | 0 | 0 | 0 | 0 | 5,8 |
| 1997-2 | 1 | 1 | 0 | 0 | 5,7 |
| 1997-3 | 2 | 0 | 1 | 0 | 5,4 |
| 1997-4 | 3 | 0 | 0 | 1 | 6,7 |
| 1998-1 | 4 | 0 | 0 | 0 | 6,9 |
| 1998-2 | 5 | 1 | 0 | 0 | 6,0 |
| 1998-3 | 6 | 0 | 1 | 0 | 6,0 |
| 1998-4 | 7 | 0 | 0 | 1 | 7,0 |
| … | … | … | … | … | … |
Om vi kör den här regressionen i ett statistiskt programpaket så får vi följande resultat:
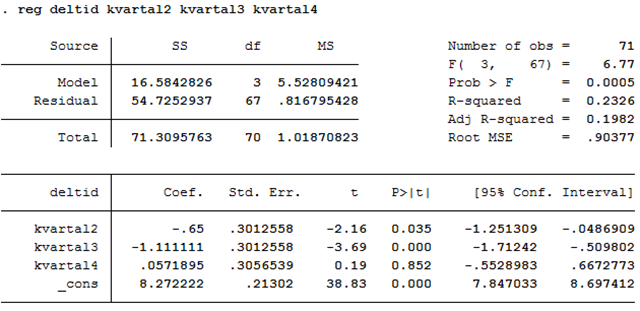
\[\widehat{deltid} = 8,27 - 0,65kvartal2 - 1,11kvartal3 + 0,06kvartal4\]
Vi kan använda den här regressionen för att prediktera procenten deltidsanställda för olika kvartal. För det första kvartalet blir prediktionen 8,27 procent:
\[\widehat{deltid} = 8,27 - 0,65\underbrace{kvartal2}_{=0} - 1,11\underbrace{kvartal3}_{=0} + 0,06\underbrace{kvartal4}_{=0} = 8,27\]
Detta är bara medelvärdet beräknat över alla observationer i första kvartalet.
I andra kvartalet predikteras andelen deltidsanställda vara 7,62 procent:
\[\widehat{deltid} = 8,27 - 0,65\underbrace{kvartal2}_{=1} - 1,11\underbrace{kvartal3}_{=0} + 0,06\underbrace{kvartal4}_{=0} = 7,62\]
Och på motsvarande sätt kan vi räkna ut prediktionerna för kvartal tre (7,16 procent) och kvartal fyra (8,33 procent).
Om vi ritar upp tidsserien tillsammans med dessa prediktioner så får vi följande figur:
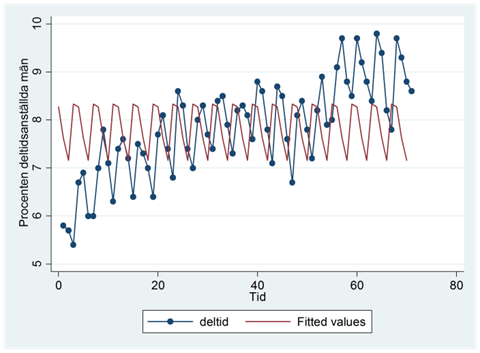
Som du ser så var detta inte särskilt lyckat. Men kanske kan vi kombinera regressionen med kvartalsdummyn och regressionen med den linjära trenden, för att på så vis få en regression som beaktar bägge aspekterna:
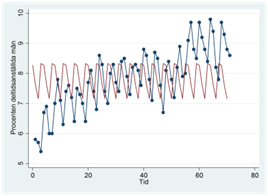
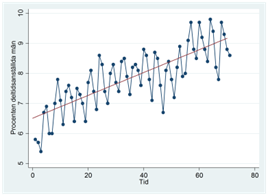
Svaret är “ja”. Vi kör då följande regression:
\[\widehat{deltid} = a + b_{1}kvartal2 + b_{2}kvartal3 + b_{3}kvartal4 + b_{4}tid\]
Vilket ger resultatet:
\[\widehat{deltid} = 6,96 - 0,69kvartal2 - 1,19kvartal3 + 0,018kvartal4 + 0,039tid\]
Vi kan använda den här regressionen för att prediktera procenten deltidsanställda i varje tidsperiod. I figuren nedan har vi ritat ut dessa prediktioner (i rött) tillsammans med tidsserien (i blått):
Sammanfattning
Övningsuppgifter
Tidsseriediagram och utjämning
- En omdebatterad utveckling under 90-talet gäller den snabba ökningen i VD-löner. Tabellen nedan visar genomsnittlig kompensation för direktörer på de största amerikanska aktiebolagen. (Med kompensation avses här både löner samt bonusar och förmåner.) Alla siffror är justerade för inflation.
| År | Kompensation (miljoner dollar) |
|---|---|
| 1993 | 3,7 |
| 1994 | 4,4 |
| 1995 | 4,8 |
| 1996 | 7,0 |
| 1997 | 9,1 |
| 1998 | 10,7 |
| 1999 | 12,7 |
| 2000 | 17,4 |
| 2001 | 14,3 |
| 2002 | 10,3 |
| 2003 | 9,1 |
Beräkna ett centrerat glidande medelvärde för år 1997. Använd tre år för att skapa detta medelvärde.
Beräkna nu ett centrerat glidande medelvärde för 2000, men utnyttja fem år.
- Hur stor andel av kvinnliga finländska arbetstagare jobbar på tillfälliga kontrakt? Tabellen nedan visar denna procent från det första kvartalet 2012 till det tredje kvartalet 2014. Beräkna ett säsongsutjämnat glidande medelvärde för det tredje kvartalet år 2013.
| År | Kvartal | Tillfälligt kontrakt (%) |
|---|---|---|
| 2012 | 1 | 16,5 |
| 2012 | 2 | 20,6 |
| 2012 | 3 | 19,2 |
| 2012 | 4 | 17,1 |
| 2013 | 1 | 16,1 |
| 2013 | 2 | 19,6 |
| 2013 | 3 | 20,0 |
| 2013 | 4 | 18,1 |
| 2014 | 1 | 17,0 |
| 2014 | 2 | 19,9 |
| 2014 | 3 | 19,8 |
- Tabellen nedan visar antalet konkurser (konk) per månad under åren 1990-1992. Data gäller Finland.
| År | Månad | Konk | År | Månad | Konk | År | Månad | Konk |
|---|---|---|---|---|---|---|---|---|
| 1990 | jan | 311 | 1991 | jan | 553 | 1992 | jan | 636 |
| 1990 | feb | 237 | 1991 | feb | 533 | 1992 | feb | 626 |
| 1990 | mars | 244 | 1991 | mars | 515 | 1992 | mars | 650 |
| 1990 | april | 208 | 1991 | april | 476 | 1992 | april | 565 |
| 1990 | maj | 336 | 1991 | maj | 547 | 1992 | maj | 520 |
| 1990 | juni | 287 | 1991 | juni | 421 | 1992 | juni | 563 |
| 1990 | juli | 239 | 1991 | juli | 450 | 1992 | juli | 485 |
| 1990 | aug | 353 | 1991 | aug | 505 | 1992 | aug | 610 |
| 1990 | sep | 273 | 1991 | sep | 555 | 1992 | sep | 698 |
| 1990 | okt | 433 | 1991 | okt | 589 | 1992 | okt | 680 |
| 1990 | nov | 439 | 1991 | nov | 576 | 1992 | nov | 657 |
| 1990 | dec | 274 | 1991 | dec | 535 | 1992 | dec | 701 |
Beräkna ett säsongsutjämnat glidande medelvärde för november 1991.
Anta nu att du har beräknat säsongsutjämnade glidande medelvärden för hela serien. Vilket är det sista datumet (År, Månad) som detta medelvärde kan beräknas?
Att beskriva trender över tid
- Tidsseriediagrammet nedan visar livslängden bland finska män mellan åren 1971 och 2014. Vi kan beskriva den linjära tidstrenden genom regressionen: \(\widehat{livslängd} = 66,421 + 0,267 \times tid\), där tid är en variabel som antar värdet 0 år 1971, värdet 1 år 1972, värdet 2 år 1973, osv.
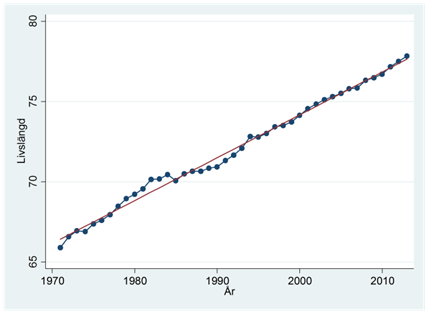
- Hur mycket har livslängden i snitt ökat per decennium?
- Tolka interceptet.
- Använd regressionslinjen för att göra en prognos för livslängden år
- Se figuren nedan. Här gäller att y ökat med 20 procent per år om vi bortser från slumpmässiga fluktuationer från den trenden.
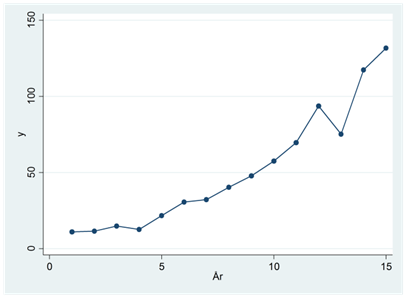
Vilken regression passar bäst för att beskriva den här utvecklingen:
\(\widehat{y} = a + b \times år\)
\(\widehat{ln(y)} = a + b \times år\)
\(\widehat{y} = a + b_{1} \times år + b_{2} \times {år}^{2}\)
\(\widehat{y} = a + b \times ln(år)\)
- Se figuren nedan. Bortsett från slumpmässiga fluktuationer så gäller här att y ökat med 5 enheter mellan år 0 och 1; med 6 enheter mellan år 1 och år 2; med 7 enheter mellan år 2 och år 3, osv.
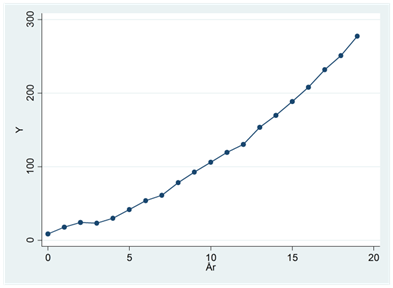
Vilken regression passar bäst för att beskriva den här utvecklingen:
\(\widehat{y} = a + b \times år\)
\(\widehat{ln(y)} = a + b \times år\)
\(\widehat{y} = a + b_{1} \times år + b_{2} \times {år}^{2}\)
\(\widehat{y} = a + b \times ln(år)\)
- Diagrammet nedan beskriver utvecklingen i ett företags årliga försäljning mellan 2001 och 2020. Vi har också anpassat följande regression till data:
\[\widehat{försäljning} = 1001 - 6,72tid + 0,589{tid}^{2}\]
där variabeln tid antar värdet 0 år 2001, värdet 1 år 2002, värdet 2 år 2003, osv.
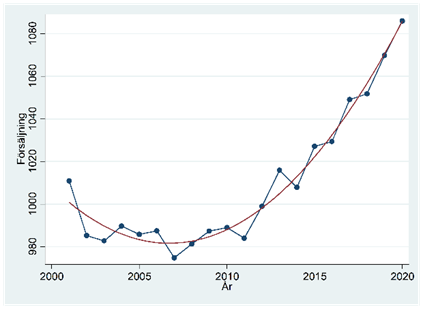
Ge en tolkning av interceptet.
Använd regressionen för att göra en prognos för år 2021.
Vilket år nåddes botten (enligt regressionen)?
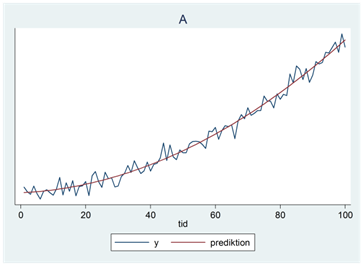
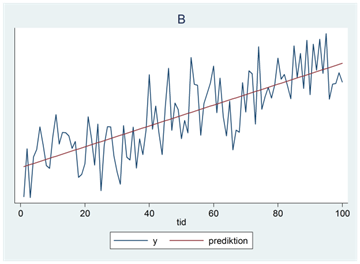
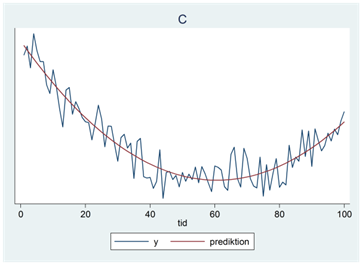
- Nedan ser du fyra tidsserier (A, B, C och D). En av trenderna beskrivs av ekvationen \(\widehat{y} = 44 - 11,9tid - 1,1{tid}^{2}\); en annan av ekvationen \(\widehat{y} = 14 + 1,1tid + 0,1{tid}^{2}\); en tredje av ekvationen \(\widehat{y} = 20 - 12,1tid + 0,1{tid}^{2}\) och en fjärde av ekvationen \(\widehat{y} = 16 + 1,5tid + 0,0{tid}^{2}\). Para ihop rätt tidsseriediagram med rätt ekvation.
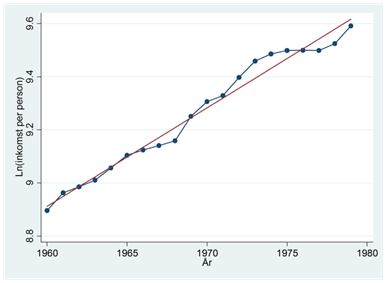
- Nedan visas trenden i logaritmerad inkomst per person för Finland mellan åren 1960 till 1979. Inkomsterna är justerade för inflation. Regressionslinjen ges av: \(\widehat{ln(inkomst)} = - 63,74 + 0,037år\). Hur många procent har inkomsterna i snitt ökat per år under den här perioden?
- Figuren nedan visar procenten kvinnor som jobbar på tillfälliga kontrakt mellan första kvartalet år 1997 till tredje kvartalet år 2014.
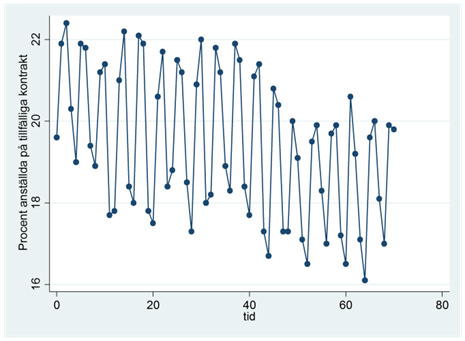
Där variabeln tid antar värdet 0 det första kvartalet år 1997; värdet 1 det andra kvartalet år 1997, värdet 2 det tredje kvartalet år 1997, osv. Vi anpassar nu en rät trendlinje till data samt inkluderar kvartalsdummyn:
\[\widehat{procent} = 18,89 - 0,0356tid + 3,25kvartal2 + 3,34kvartal3 + 0,49kvartal4\]
där procent mäter procenten kvinnor anställda på tillfälliga kontrakt; kvartal2 är en dummy för det andra kvartalet; kvartal3 är en dummy för tredje kvartalet och kvartal4 är en dummy för det fjärde kvartalet.
I vilket kvartal är andelen kvinnor anställda på tillfälliga kontrakt som högst? I vilket kvartal är denna andel som lägst?
Använd den här regressionen för att göra prognoser för de två påföljande kvartalen (fjärde kvartalet 2014 och första år 2015).
- Du jobbar på ett företag och chefen ber dig att beskriva trenden i försäljningssiffrorna över de senaste åtta åren. Du anpassar en rät trendlinje till data:
\[\widehat{försäljning} = a + b \times tid\]
Där variabeln tid antar värdet 0 det första kvartalet i data, värdet 1 det andra kvartalet, värdet 2 det tredje kvartalet, …, värdet 5 det första kvartalet därpå följande år, osv.
Du ritar upp data i ett tidsseriediagram och ser en tydlig säsongsvariation. Beskriv en regressionsekvation som dessutom beaktar säsongsvariationen. (Glöm inte att också beskriva vad dina variabler mäter.)
Chefen ber dig nu att se om försäljningen ökat efter att han blev chef för tre år sedan. Beskriv en regressionsekvation som dessutom mäter detta.