12 Test av samband i korstabeller
Hittills har vi sett många exempel på hur kan testa för olika sorters samband i data. Men i alla exempel hittills så har utfallsvariabeln varit kvantitativ (såsom löner, provresultat, priser eller livslängd), dvs. sådana variabler som naturligt mäts på en numerisk skala. I det här kapitlet så ska vi se hur man kan testa om det finns signifikanta samband mellan två kvalitativa variabler. Här är några exempel:
Finns det ett samband mellan kön och partipreferens?
Är det vanligare med skilsmässor bland personer med låg socioekonomisk status än bland sådana med hög?
I USA gäller att personer som är negativa till aborter också ofta är positiva till skattelättnader. Finns det också ett sådant samband i Finland?
Vad karaktäriserar personer som inte röstar i politiska val? Kön? Ointresse för politik? Att man är nöjd med läget som det är?
26. Chi2-tester
12.1 Korstabeller
Korstabeller används för att beskriva sambandet mellan två kvalitativa variabler.
Exempel. Är professionella placerare bättre på att sätta ihop en aktieportfölj än studenter? Vi har gjort ett experiment där 80 studenter och 20 professionella placerare fått sätta ihop aktieportföljer (var och en har satt ihop en egen portfölj). En månad senare mäter vi om aktieportföljerna ligger på plus eller minus. Bland studenterna ligger 22 portföljer på minus och 58 på plus. Bland proffsen ligger 3 portföljer på minus och 17 på plus:
| MINUS | PLUS | |
| STUDENTERNA | 22 | 58 |
| PROFFSEN | 3 | 17 |
Finns det ett samband mellan variablerna? Ja, i samplet ser vi ett samband; proffsen har slutat på plus i 85 procent av fallen och studenterna i 72,5 procent. Men är skillnaden signifikant? Eller skulle den kunna skyllas på slumpen? Om du gissar att denna skillnad skulle kunna skyllas på slumpen så har du rätt. Lite längre fram så kommer vi att testa detta mer formellt.
Exempel. Finns det ett samband mellan träning och psykisk ohälsa?
| TRÄNAR EJ | TRÄNAR 1 GÅNG/VECKA | TRÄNAR 2+ GÅNGER/VECKA | |
| DEPRIMERAD | 65 | 25 | 10 |
| EJ DEPRIMERAD | 120 | 120 | 60 |
Samplet innehåller 100 deprimerade, varav 65 procent inte tränar; 25 procent tränar 1 gånger per vecka och 10 procent tränar minst 2 gånger per vecka. Samplet innehåller också 300 som inte är deprimerade, varav 40 procent inte tränar; 40 procent tränar 1 gång per vecka och 20 procent tränar minst 2 gånger per vecka. Att inte träna alls är alltså vanligare bland de deprimerade; att träna en eller två gånger per vecka är vanligare bland de som inte är deprimerade. Det verkar alltså finnas ett samband åtminstone i samplet – men är det statistiskt signifikant?
Exempel. Är kvinnor mer benägna att rösta rött än män? Vi har samlat in ett datamaterial för 100 personer; 50 män och 50 kvinnor. Bland männen är det 30 som röstar blått och 20 som röstar rött. Bland kvinnorna är förhållet det omvända; 20 röstar blått och 30 röstar rött.
| BLÅTT | RÖTT | |
| MÄN | 30 | 20 |
| KVINNOR | 20 | 30 |
Vi ser att det finns ett samband mellan variablerna i samplet; medan 60 procent av kvinnorna röstar rött så är det bara 40 procent av männen som röstar rött. Men är detta samband signifikant? Eller skulle det kunna skyllas på slumpen? För att testa detta så kan vi använda Pearsons chi2-test.
12.2 Chi2-testet
I det här skedet ska vi bara se hur chi2-värdet beräknas (chi2 uttalas ki-två eller ki-i-kvadrat). Det kommer så småningom att bli klart hur vi använder denna test-statistika.
Nedan visas formeln för chi2-värdet:
\[\chi^{2} = \sum_{celler}^{}\frac{{(O_{c} - F_{c})}^{2}}{F_{c}}\]
O är här en observerad frekvens; F är en förväntad frekvens. Vi ser bäst vad dessa frekvenser mäter genom ett exempel.
Exempel. Tabellen nedan visar hur många som röstar rött och blått och hur detta skiljer sig mellan könen. Detta är de observerade frekvenserna.
| BLÅTT | RÖTT | |
| MÄN | 30 | 20 |
| KVINNOR | 20 | 30 |
De förväntade frekvenserna visar hur vi skulle förvänta oss att den här korstabellen såg ut om det inte finns något samband mellan kön och partipreferens. I korstabellen nedan har vi beskrivit de förväntade frekvenserna inom parentes.
| BLÅTT | RÖTT | |
| MÄN | 30 (25) | 20 (25) |
| KVINNOR | 20 (25) | 30 (25) |
50 procent röstar blått (totalt sett). Om det inte finns nåt samband så skulle vi alltså förvänta oss att 50 procent av männen röstar blått och 50 procent av kvinnorna, vilket skulle betyda 25 män och 25 kvinnor. På motsvarande sätt förväntas 25 män och 25 kvinnor rösta rött.
Vi kan nu se ut att chi2-värdet är 4:
\[\chi^{2} = \sum_{celler}^{}\frac{{(O_{c} - F_{c})}^{2}}{F_{c}}\]
\[= \frac{\left( O_{1} - F_{1} \right)^{2}}{F_{1}} + \frac{\left( O_{2} - F_{2} \right)^{2}}{F_{2}} + \frac{\left( O_{3} - F_{3} \right)^{2}}{F_{3}} + \frac{\left( O_{4} - F_{4} \right)^{2}}{F_{4}} =\]
\[\frac{{(30 - 25)}^{2}}{25} + \frac{{(20 - 25)}^{2}}{25} + \frac{{(20 - 25)}^{2}}{25} + \frac{{(30 - 25)}^{2}}{25} = 4\]
Exempel. Hur ser de förväntade frekvenserna ut i detta fall?
| TRÄNAR EJ | TRÄNAR 1 GÅNG/VECKA | TRÄNAR 2+ GÅNGER/VECKA | |
| DEPRIMERAD | 65 | 25 | 10 |
| EJ DEPRIMERAD | 120 | 120 | 60 |
Samplet innehåller totalt 400 personer varav 185 inte tränar alls; det är alltså frågan om 46,25 procent av samplet. Alltså skulle vi förvänta oss att 46,25 procent av de deprimerade – och 46,25 procent av de icke-deprimerade – inte tränar alls. Det skulle då vara frågan om 46,25 personer bland de deprimerade (som är 100 till antalet) och 138,75 bland de icke-deprimerade (som är 300 till antalet). Tabellen nedan ger alla förväntade frekvenser inom parentes. Kan du räkna ut chi2-värdet utifrån formeln? (Rätt svar är 19,076.)
| TRÄNAR EJ | TRÄNAR 1 GÅNG/VECKA | TRÄNAR 2+ GÅNGER/VECKA | |
| DEPRIMERAD | 65 (46,25) | 25 (36,25) | 10 (17,5) |
| EJ DEPRIMERAD | 120 (138,75) | 120 (108,75) | 60 (52,5) |
Chi2-fördelningen
Chi2-värdet (\(\chi^2\)) blir alltid minst noll. Och ju mer de observerade frekvenserna avviker från de förväntade, desto större chi2-värde. Då chi2-värdet blir tillräckligt stort så säger vi att sambandet är signifikant. I exemplet med mäns och kvinnors partipreferens fick vi ett chi2-värde på 4. Är detta tillräckligt stort? För att ta reda på det ska vi beräkna:
\(p\)-värdet \(= P(\chi^2 \geq 4)\)
Denna beräkning görs enklast av datorer. Online-kalkylatorn nedan visar att p-värdet är 0,0455. Det finns alltså ett signifikant samband mellan kön och partipreferens.
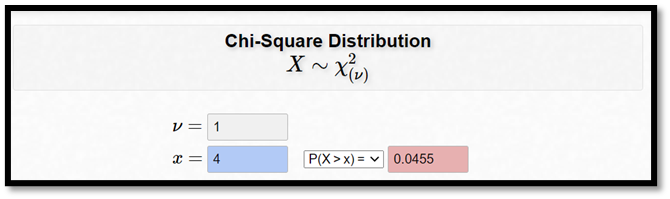
Figuren nedan illustrerar denna chi2-fördelning.
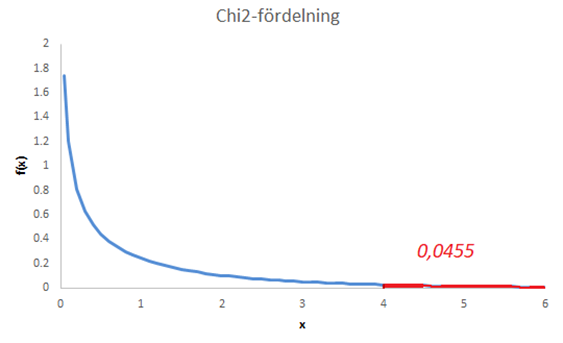
Om det inte finns något samband mellan kön och partipreferens så får vi ett sampel där chi2-värdet hamnar någonstans mellan 0 och 3,84 i 95 procent av fallen. Om vi får ett sampel där chi2-värdet hamnar någonstans inom detta intervall så säger vi att resultatet är insignifikant; det observerade sambandet i samplet är då så pass otydligt att det skulle kunna skyllas på slumpen. I 5 procent av fallen får vi ett sampel där chi2-värdet blir större än 3,84; i dessa fall så säger vi att resultatet är signifikant (p-värdet < 0,05). Men vi fick ett chi2-värde på 4 vilket gav oss ett p-värde på 0,0455.
Chi2-fördelningens utseende varierar från fall till fall. Sannolikheten för att – bara av slumpen – få ett chi2-värde på minst 4 beror också på hur många rader och kolumner vi har i vår korstabell. Vi säger att chi2-fördelningen har en parameter som bestämmer exakt hur den ut. Den parametern benämns frihetsgradsantalet. Frihetsgradsantalet fås genom att ta (r-1)*(k-1) där r är antalet rader och k är antalet kolumner. Här är några grafiska exempel:
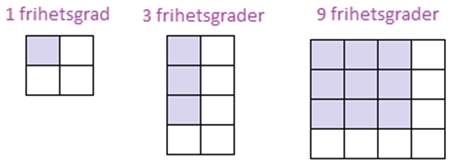
I exemplet med kön och partipreferens har vi alltså 1 frihetsgrad:
| BLÅTT | RÖTT | |
| MÄN | 30 | 20 |
| KVINNOR | 20 | 30 |
Men säg att vi istället haft följande korstabell:
| C | SDP | Gröna | KD | Saml | Sannf | SFP | Vf | |
|---|---|---|---|---|---|---|---|---|
| MÄN | … | … | … | … | … | … | … | … |
| KVINNOR | … | … | … | … | … | … | … | … |
Här har vi 7 frihetsgrader. Den här chi2-fördelningen visas nedan.
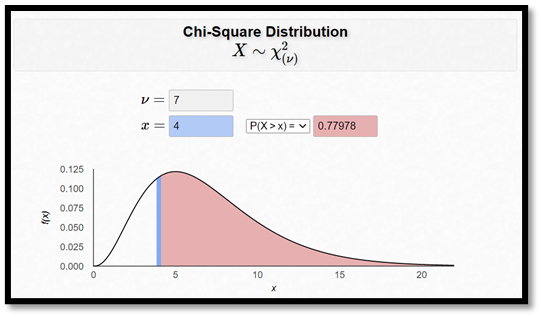
Med så många celler i vår korstabell så skulle ett chi2-värde på 4 inte längre vara något anmärkningsvärt; p-värdet hade då blivit 0,780.
Exempel. Är professionella placerare bättre på att sätta ihop en aktieportfölj än studenter?
| MINUS | PLUS | |
| STUDENTERNA | 22 | 58 |
| PROFFSEN | 3 | 17 |
Hur ser de förväntade frekvenserna ut? Jo, i 25 procent av fallen har portföljerna slutat på minus (25 av totalt 100 portföljer). Om det inte finns något samband mellan variablerna, så skulle vi alltså förvänta oss att 25 procent av studenternas portföljer skulle sluta på minus och 25 procent av proffsens. Studenterna har totalt 80 portföljer så 20 portföljer (dvs. 25 procent) förväntas gå på minus. Proffsen har totalt 20 portföljer så 5 portföljer (dvs. 25 procent) förväntas gå på minus. På motsvarande sätt skulle vi förvänta oss att 75 procent av studenternas portföljer skulle sluta på plus, och 75 procent av proffsens. Detta ger oss de förväntade frekvenserna inom parentes:
| MINUS | PLUS | |
|---|---|---|
| STUDENTERNA | 22 (20) | 58 (60) |
| PROFFSEN | 3 (5) | 17 (15) |
Och chi2-värdet blir 1,333… :
\[\chi^{2} = \sum_{celler}^{}{\frac{{(O_{c} - F_{c})}^{2}}{F_{c}} =}\]
\[\frac{{(22 - 20)}^{2}}{20} + \frac{{(58 - 60)}^{2}}{60} + \frac{{(3 - 5)}^{2}}{5} + \frac{{(17 - 15)}^{2}}{15} \approx 1,333\]
Med hjälp av ett statistiskt programpaket kan vi förstås bespara oss besväret att räkna ut chi2-värdet manuellt. Nedan beskrivs resultatet från SPSS.
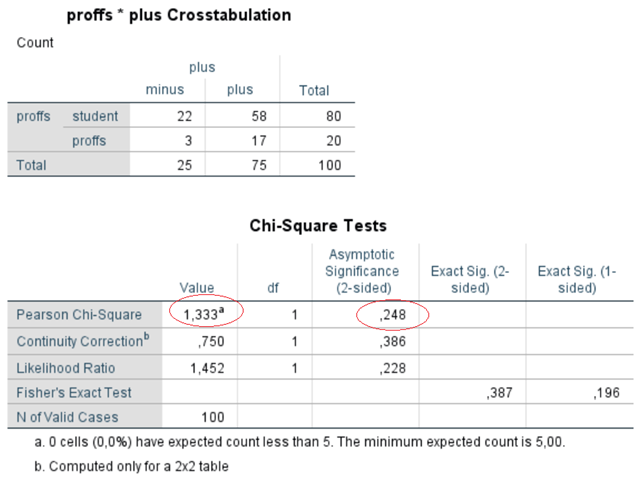
Chi2-värdet är 1,333 och p-värdet är 0,248. Sambandet är alltså inte signifikant. Följande online-kalkylator ger oss samma resultat:
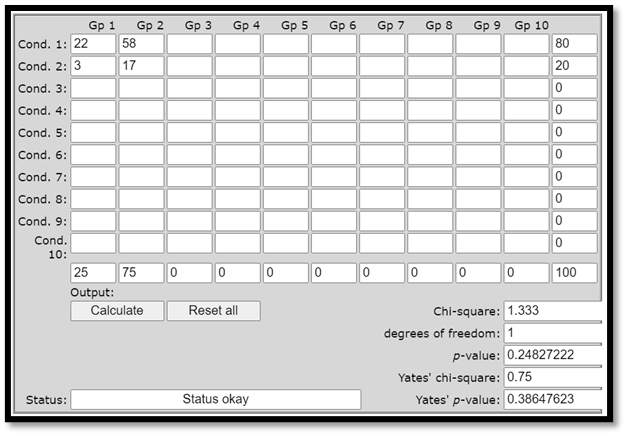
Exempel. Är sambandet mellan träning och psykisk ohälsa signifikant?
| TRÄNAR EJ | TRÄNAR 1 GÅNG/VECKA | TRÄNAR 2+ GÅNGER/VECKA | |
| DEPRIMERAD | 65 | 25 | 10 |
| EJ DEPRIMERAD | 120 | 120 | 60 |
Matar in data i kalkylatorn med resultatet:
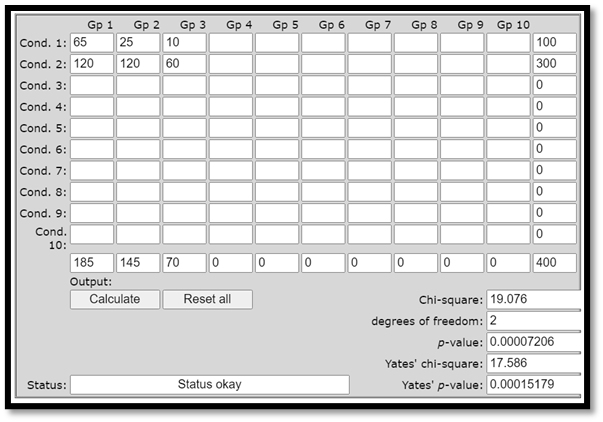
Svaret är ja: Chi2-värdet är 19,076 och p-värdet är 0,000072… . Sambandet är alltså signifikant också på 1-procentsnivån.
Notera här att chi2-testet också anger vår status (“Status okay”). Chi2-testet bygger nämligen på följande två antaganden:
Slumpmässigt sampel (oberoende dragningar)
Tillräckligt många observationer i varje cell. En tumregel brukar vara en förväntad frekvens på minst 5 i varje cell, eller att max 20 procent av cellerna har en förväntad frekvens som är mindre än 5.
Det är alltså det andra antagandet som kalkylatorn ovan testat. Om detta antagande inte är uppfyllt så finns det alternativa tester (såsom Fishers exakta test) men vi lämnar den diskussionen i detta skede.
12.3 Chi2-testet för fördelningsform
Exempel. Nedan visas data hämtat från artikeln Sociodemographic risk factors in wife abuse: Results from a Survey of Toronto Women. Tabellen visar åldersfördelningen för 490 samplade kvinnor.
| Ålder | Observerad frekvens |
|---|---|
| 20–24 | 103 |
| 25–34 | 216 |
| 35–44 | 171 |
| Totalt | 490 |
Författarna skriver att de försökt dra ett slumpmässigt sampel genom att ringa slumpmässigt utvalda hushåll. Har detta lyckats? Enligt folkbokföringen så gäller följande åldersfördelning bland kvinnor i Toronto i åldern 20 till 44:
| Ålder | Procent |
|---|---|
| 20–24 | 18 |
| 25–34 | 50 |
| 35–44 | 32 |
| Totalt | 100 |
Har författarna lyckats dra ett slumpmässigt sampel? Eller finns det en signifikant skillnad mellan åldersfördelningen i samplet och den i populationen? Vi kan använda chi2-testet för att svara på detta.
Vi börjar med att fylla i de förväntade frekvenserna:
| Ålder | Observerad frekvens | Förväntad frekvens |
|---|---|---|
| 20–24 | 103 | 88,2 |
| 25–34 | 216 | 245 |
| 35–44 | 171 | 156,8 |
| Totalt | 490 | 490 |
Eftersom populationen till 18 procent består av 20-24-åringar, så förväntas 18 procent av personerna i samplet vara 20-24 år. Vi har totalt 490 personer i samplet; 88,2 av dessa förväntas vara 20-24 år (0,18*490 = 88,2). Detta är den förväntade frekvensen på första raden. På samma sätt har vi fått de andra två förväntade frekvenserna.
Vi kan nu räkna ut att chi2-värdet är 7,202:
\[\chi^{2} = \sum_{}^{}\frac{{(O - F)}^{2}}{F}\]
\[= \frac{{(103 - 88,2)}^{2}}{88,2} + \frac{{(216 - 245)}^{2}}{245} + \frac{{(171 - 156,8)}^{2}}{156,8} \approx 7,202\]
Är 7,202 ett tillräckligt stort värde för att vi ska kunna säga att skillnaden är signifikant? Kalkylatorn nedan visar att svaret är ja; p-värdet är 0,027.
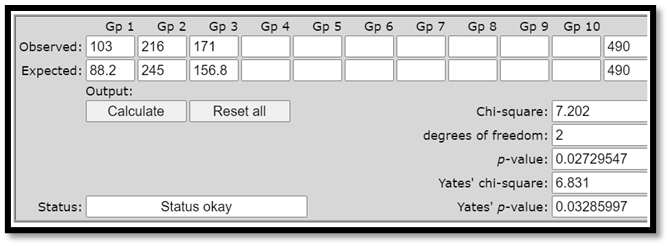
Övningsuppgifter
Chi2-testet
- Den här uppgiften är inspirerad av ett experiment som gjordes på 70-talet. Vi låter 500 barn i förskoleåldern genomgå följande test. En försöksledare ger barnet en marshmallow, med löftet om att denna ska få ytterligare en marshmallow om hon eller han väntar med att äta upp den första tills försöksledaren kommer tillbaka. Därefter går försöksledaren ut ur rummet och återvänder 10 minuter senare. 40 procent av barnen orkade vänta. I korstabellen nedan kallas dessa “tålmodiga”. Därefter mäter vi hur många av barnen som slutligen började studera på ett universitet.
| EJ UNIVERSITET | UNIVERSITET | |
| OTÅLIG | 240 | 60 |
| TÅLMODIG | 120 | 80 |
Anta att nollhypotesen är sann så att det inte finns något samband mellan variablerna. Hur ser då de förväntade frekvenserna ut?
[Kräver online-kalkylator] Är sambandet signifikant? I så fall, på vilken nivå?
- [Kräver online-kalkylator] Tabellen nedan visar hur många som överlevde och dog i Titanic beroende på om de reste i första, andra eller tredje klass. Är sambandet signifikant? I så fall, på vilken nivå? (Testa också att du kan bekräfta att den förväntade frekvensen i översta rutan till vänster är ungefär 199,6.)
| ÖVERLEVDE INTE | ÖVERLEVDE | |
| FÖRSTA KLASS | 123 | 200 |
| ANDRA KLASS | 158 | 119 |
| TREDJE KLASS | 528 | 181 |
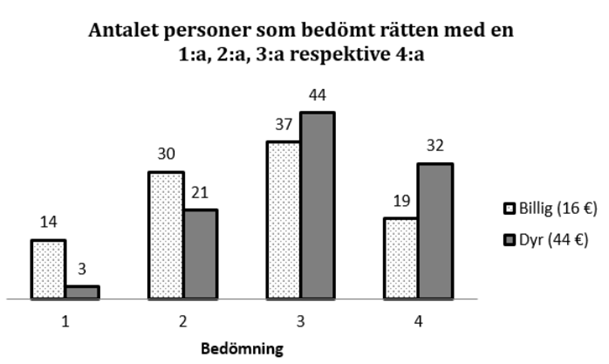
- [Kräver online-kalkylator] Hur mycket av vår smakupplevelse är psykologi? Vi låter 200 personer genomgå följande test. De bjuds på en middag på en fin restaurang och ska sedan bedöma hur bra rätten smakade på en skala mellan 1 och 4 (högre vitsord = bättre). 100 personer lottas ut och dessa får veta att rätten vanligtvis kostar 44 euro. De övriga 100 får veta att rätten vanligtvis kostar 16 euro. (Alla äter dock exakt samma rätt.) Stapeldiagrammet nedan beskriver hur de två grupperna bedömt rätten. Finns det signifikanta skillnader i bedömning beroende på om man fått höra att rätten är dyr eller billig?
Chi2-testet för fördelningsform
- Du vill göra en studie om pensionärernas ekonomi och hälsa. Du samplar slumpmässigt 200 pensionärer som får besvara en enkät. Det visar sig dock att enbart 60 procent av de samplade personerna svarar. Kan samplet fortfarande betraktas som slumpmässigt draget? Tabellen nere till vänster visar pensionärernas åldersfördelning enligt folkbokföringen. Till höger ges ditt datamaterial.
Folkbokföringen
| Ålder | Procent |
|---|---|
| 50–59 | 18 |
| 60–69 | 30 |
| 70–79 | 28 |
| 80+ | 24 |
| Totalt | 100 |
Samplet
| Ålder | Frekvens |
|---|---|
| 50–59 | 15 |
| 60–69 | 44 |
| 70–79 | 40 |
| 80+ | 21 |
| Totalt | 120 |
Vilka åldersgrupper är underrepresenterade i ditt sampel (i förhållande till hur vi skulle förvänta oss att samplet såg ut)? Vilka åldersgrupper är överrepresenterade?
[Kräver online-kalkylator] Finns det en signifikant skillnad mellan samplets fördelning och folkbokföringens?
- [Kräver online-kalkylator] En magiker har en tärning. Du vill testa om den är riggad och kastar tärningen 300 gånger med följande resultat:
| Utfall | Frekvens |
|---|---|
| 1 | 46 |
| 2 | 53 |
| 3 | 50 |
| 4 | 49 |
| 5 | 61 |
| 6 | 41 |
Finns det stöd i data för att påstå att tärningen är riggad?