| id | kvinna | längd | vikt |
|---|---|---|---|
| 1 | 1 | 171 | 77 |
| 2 | 0 | 174 | 84 |
| 3 | 1 | 167 | 74 |
| 4 | 1 | 166 | 55 |
| 5 | 0 | 184 | 70 |
| … | … | … | … |
| 200 | 0 | 191 | 90 |
6 Multipel regressionsanalys
I kapitel 4 tittade vi på enkel regressionsanalys som visar hur utfallsvariabeln varierar som en funktion av en oberoende variabel:
\[\widehat{y} = a + bx\]
Anta att y är priset för en lägenhet och att x är antalet sovrum. Regressionslinjen visar då hur priset varierar med antalet sovrum. Vi kan exempelvis använda regressionslinjen för att uppskatta hur mycket vi kan tjäna på att sälja en lägenhet med tre sovrum. Men vi vet också att priset beror på flera andra faktorer, såsom lägenhetens läge, husets byggnadsår och kvalitét, osv. I en multipel regression inkluderar vi flera sådana oberoende variabler (x1, x2, …, xk):
\[\widehat{y} = a + b_{1}x_{1} + b_{2}x_{2} + \ldots + {b_{k}x}_{k}\]
Genom att ta in flera oberoende variabler så kan vi få mer träffsäkra prediktioner. Anta att lägenheten i fråga är nybyggd och har havsutsikt. Om vi bara beaktar att lägenheten har tre sovrum så kommer vi antagligen att underskatta försäljningspriset, men om vi dessutom beaktar lägenhetens andra egenskaper så får vi sannolikt en uppskattning som stämmer bättre överens med lägenhetens faktiska försäljningspris.
Som det här exemplet visar så kan vi använda multipel regressionsanalys för att få mer träffsäkra prediktioner. Men vanligtvis använder vi multipel regressionsanalys i ett annat syfte; för att kontrollera för inflytandet hos bakomliggande faktorer. Vi ska nu se vad det betyder.
10. Multipel regressionsanalys, del 1
11. Multipel regressionsanalys, del 2
6.1 Att kontrollera för andra faktorer
Exempel. Vi samplar 200 personer och mäter hur mycket de väger. Regressionen nedan visar att männen i genomsnitt väger 79 kilo, och att kvinnorna i snitt väger 13 kilo mindre:
\[\widehat{vikt} = 79 - 13kvinna\]
Varför väger kvinnor mindre än män? En viktig orsak är antagligen att kvinnor i snitt är kortare än män. Anta nu att vi också har data för personernas längder. Vi har då möjlighet att ställa oss följande fråga: Om vi jämför kvinnor och män som är lika långa, ser vi då fortfarande en skillnad i vikt mellan könen?
Vi kan få en uppskattning av svaret på den här frågan genom att inkludera längden som en oberoende variabel i regressionen:
\[\widehat{vikt} = a + b_{1}kvinna + b_{2}längd\]
Ett utdrag av data visas nedan:
Hur kan vi på bästa sätt använda data för att beräkna värdena för a, b1 och b2 i regressionsekvationen? Precis som vid enkel regression så använder vi minsta-kvadratmetoden (OLS). OLS ger oss en regressionsekvation som uppskattar hur medelvärdet för utfallsvariabeln (y) varierar med x-variablerna. I en multipel regression är det dock tidskrävande att räkna ut koefficienternas värden för hand. Här överlåter vi jobbet till datorer (se Appendix för formlerna). Detta ger oss resultatet:
\[\widehat{vikt} = - 46 - 4kvinna + 0,7längd\]
där \(\widehat{vikt}\) är den predikterade vikten, dvs. en uppskattning av hur genomsnittlig vikt varierar beroende på kön och längd. Vi kan använda den här regressionen för att prediktera vikten för personer med olika egenskaper:
En kvinna som är 170 centimeter predikteras väga 69 kilo:
\[\widehat{vikt} = - 46 - 4\underbrace{kvinna}_{=1} + 0,7\underbrace{längd}_{= 170} = 69\]
En man som är 170 centimeter predikteras väga 73 kilo:
\[\widehat{vikt} = - 46 - 4\underbrace{kvinna}_{= 0} + 0,7\underbrace{längd}_{= 170} = 73\]
Som du ser så predikteras en kvinna väga 4 kilo mindre än en man (69 – 73 = -4) givet att båda är lika långa. Här gör vi jämförelsen då längden sätts lika med 170 centimeter, men hade vi valt en annan längd (säg 160 centimeter) så hade viktskillnaden fortfarande varit 4 kilo. Det här visar hur vi tolkar koefficienten för kvinna: Kvinnor väger i snitt 4 kilo mindre än män, givet samma längd. I en statistisk rapport skulle man vanligtvis skriva att “kvinnor väger i snitt 4 kilo mindre än män, kontrolleratför längd”.
På motsvarande sätt tolkar vi koefficienten för längd: Då längden ökar med en centimeter så ökar vikten i snitt med 0,7 kilo, kontrollerat för kön. Notera att det här är motsvarande tolkning som i en enkel regression, bara att vi nu också “kontrollerat för kön”.
Skillnaden mellan enkel och multipel regression
Exempel forts. Vi sa att kvinnor i snitt väger 4 kilo mindre än män, givet samma längd. Men hur går denna jämförelse till i praktiken? Flera personer i data är ensamma om sin längd (exempelvis är den kortaste personen i data ensam om att vara 145 centimeter). Så vad är det egentligen som händer när vi kontrollerar för längd? Som du ser nedan så ökar koefficienten för kvinna från -13 till -4, men varför?
\[\widehat{vikt} = 79 - 13kvinna\]
\[\widehat{vikt} = - 46 - 4kvinna + 0,7längd\]
Jo, männen i data är i snitt 179 centimeter långa; kvinnorna är 166. Det är en längdskillnad på 13 centimeter. Och hur mycket adderar 13 centimeter till vikten? Jo, 9 kilo: Varje centimeter adderar 0,7 kilo till vikten (13*0,7 = 9). Och 9 kilo är också hur mycket koefficienten för kvinna ökar då vi kontrollerar för längden (-13 + 9 = -4). Slutsatsen: I snitt väger kvinnor 13 kilo mindre än män, men 9 kilo av skillnaden kan förklaras av att kvinnor i snitt är 13 centimeter kortare än män.
För att få en bättre känsla för vad som händer när vi kontrollerar för något så ska vi ännu se på två exempel:
Exempel. Vi mäter sambandet mellan längd och läsförmåga för ett sampel lågstadiebarn:
\[\widehat{läsförmåga} = - 108 + 1,2 \times längd\]
där läsförmåga mäts genom ett test där man kan få allt mellan 0 och 100 poäng; längd mäts i centimeter. Från regressionen ser vi att varje extra centimeter i snitt adderar 1,2 poäng till läsförmågan. Men är det verkligen längden i sig som spelar roll? Eller är det snarare så att långa barn läser bättre eftersom de i genomsnitt är äldre? Vi kontrollerar nu för barnets ålder med resultatet:
\[\widehat{läsförmåga} = - 27 + 0,02 \times längd + 8,9 \times ålder\]
Som du ser så försvinner nu praktiskt taget hela effekten av längd. Då vi jämför barn av samma ålder så finns det med andra ord inget samband mellan längd och läsförmåga.
Exempel. Är kvinnor bättre bilförare än män? I regressionen nedan är olyckor en variabel som mäter antalet trafikolyckor som personen varit inblandad i under det senaste året; kvinna är en dummy som antar värdet 1 för kvinnor och värdet 0 för män. Regressionen visar att män i snitt varit inblandade i 0,25 trafikolyckor och att kvinnor i snitt varit inblandade i 0,15 olyckor.
\[\widehat{olyckor} = 0,25 - 0,1 \times kvinna\]
Men kanske kvinnor varit inblandade i färre trafikolyckor eftersom de kör mindre bil? Vi kontrollerar nu för antalet kilometer som personen kört per vecka:
\[\widehat{olyckor} = - 0,01 + 0,01 \times kvinna + 0,0025 \times km\]
Koefficienten för kvinna blir nu praktiskt taget noll. Då vi jämför män och kvinnor som kör lika mycket så finns det ingen skillnad i olycksfrekvens mellan könen.
Grafisk presentation
Då vi vill illustrera sambandet mellan två variabler är det naturligt att använda spridningsdiagram. Men hur kan vi presentera sambandet mellan tre variabler? En möjlighet kan vara att kombinera flera spridningsdiagram i ett. Vi ska se ett exempel på det här.
Exempel. Vi vill ta reda på om universitetsutbildning ger högre lön. Vi har ett data som består av ett hundratal personer där vissa tog en universitetsexamen efter gymnasiet, medan andra gick direkt in i arbetslivet. Vi mäter därefter genomsnittlig månadslön för dessa personer mellan 35 och 40 års ålder (variabeln lön). I regressionen nedan är uni en dummy som antar värdet 1 för personer med universitetsexamen och 0 för dem med gymnasieutbildning. Vi kontrollerar också för avgångsbetyget från gymnasiet (variabeln betyg):
\[\widehat{lön} = 900 + 500uni + 200betyg\]
I snitt tjänar universitetsutbildade 500 euro mer än gymnasieutbildade då vi kontrollerar för gymnasiebetyget. Vi ser också att lönen i snitt stiger med 200 euro för varje ytterligare betygspoäng då vi kontrollerar för utbildningsnivå. Vårt mål är att illustrera dessa två effekter grafiskt.
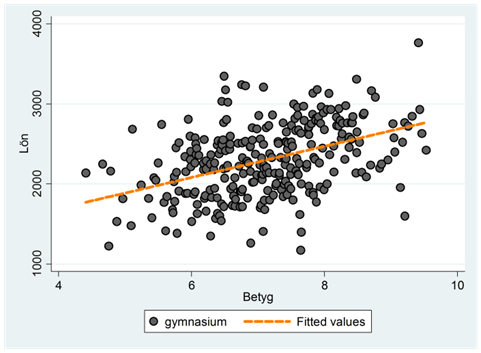
Vi vet redan hur vi kan beskriva sambandet mellan lön och betyg genom ett spridningsdiagram. Låt oss göra det, men först enbart för personer med gymnasieutbildning. För dessa beskrivs sambandet av:
\(\widehat{lön} = 900 + 500\underbrace{uni}_{= 0} + 200betyg = 900 + 200betyg\)
I spridningsdiagrammet nedan har vi ritat ut detta samband tillsammans med observationerna för den här gruppen:
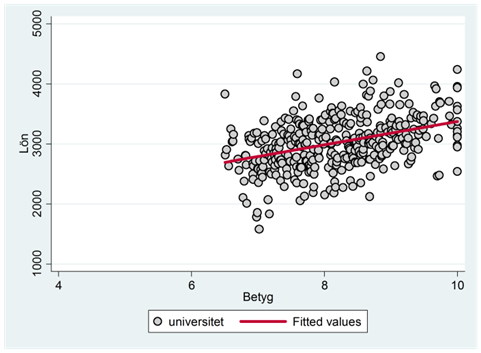
För personer med universitetsutbildning beskrivs sambandet av:
\[\widehat{lön} = 900 + 500\underbrace{uni}_{= 1} + 200betyg = 1400 + 200betyg\]
I spridningsdiagrammet nedan har vi ritat ut detta samband tillsammans med observationerna för den här gruppen:
Vi kombinerar dessa två spridningsdiagram i ett med resultatet:
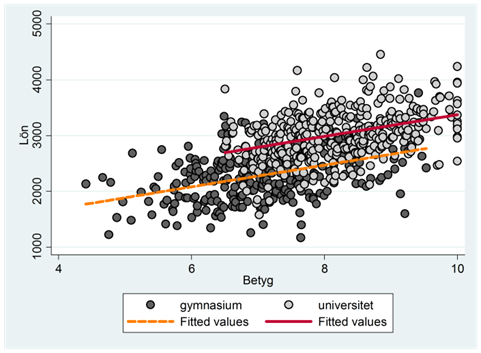
Det vertikala avståndet mellan dessa två linjer är 500 euro, dvs. den genomsnittliga löneskillnaden mellan grupperna då vi kontrollerat för gymnasiebetyget.
Förklaringsgraden
Exempel. Regressionen nedan visar hur lönen skiljer sig mellan svarta och vita basketspelare i USA:
\[\widehat{lön} = 1267 + 194,13svart\]
där lön är årslön mätt i tusentals dollar. I det här datamaterialet tjänar svarta spelare i snitt nästan 200 000 dollar mer än vita. Vi kontrollerar nu för antalet poäng som spelaren gjort per match:
\[\widehat{lön} = 278 + 12,11svart + 111,24poäng\]
När vi kontrollerar för poäng så sjunker löneskillnaden till cirka 12 000 dollar. Det här visar att svarta spelare i snitt gör något fler poäng än vita; när vi kontrollerar för antalet poäng minskar därför lönegapet. Slutligen kontrollerar vi ännu för erfarenhet (erf) och antalet returer per match (ret):
\[\widehat{lön} = - 168 - 0,61svart + 80,79poäng + 82,96erf + 77,79ret\]
I den här regressionen är löneskillnaden mellan svarta och vita spelare praktiskt taget noll. Det finns med andra ord inget lönegap efter att vi kontrollerat för ett antal relevanta skillnader i egenskaper mellan grupperna.
Om vi kör den sista regressionen i ett statistiskt programpaket så får vi ett resultat som ser ut såhär:
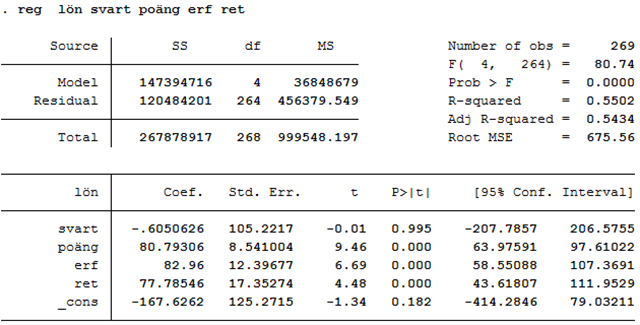
Den här regressionen är gjord i statistikprogrammet STATA, men uppställningen ser ungefär likadan ut oavsett vilket program du använder. Vi hittar variablernas koefficienter i den nedre tabellen, kolumnen Coef. Uppe till höger ges förklaringsgraden (R2) som har värdet ~0,55. Den visar att cirka 55 procent av variationen i löner kan förklaras av de oberoende variablerna (etnicitet, antalet poäng per spel, erfarenhet och antalet returer per spel). Förklaringsgraden har med andra ord motsvarande betydelse som i en enkel regression; den visar hur mycket av variationen i y-variabeln som kan förklaras av x-variablerna.
Så hur räknar vi ut förklaringsgraden? När vi har en enkel regression, dvs. en oberoende variabel, så kan vi räkna ut förklaringsgraden som kvadraten på korrelationskoefficienten. När vi har en multipel regression så kan vi göra på motsvarande sätt; förklaringsgraden är då kvadraten på korrelationskoefficienten, där korrelationskoefficienten mäter sambandet mellan y och de predikterade värdena på y. Alternativt använder vi formeln:
\[R^{2} = 1 - \frac{variansen\ i\ residualerna}{variansen\ i\ y}\]
Här kan det vara läge att fundera lite över vad en residual betyder i en multipel regression. Precis som i en enkel regression så är residualen skillnaden mellan sanningen och prediktionen. Exempel: Den första spelaren i data svart, han har gjort 24,5 poäng per spel, han har 9 års erfarenhet och har gjort 11,2 returer per spel. Predikterad lön:
\[\widehat{lön} = - 167,63 - 0,61\underbrace{svart}_{= 1} + 80,79\underbrace{poäng}_{24,5} + 82,96\underbrace{erf}_{= 9} + 77,79\underbrace{ret}_{= 11,2} \approx 3429\]
Den här spelaren predikteras tjäna 3429 enheter (dvs. ~3,4 miljoner dollar). Hans egentliga lön är 3625 enheter (~3,6 miljoner dollar). För den här spelaren är residualen alltså 196 enheter eller 196 000 dollar; han tjänar nästan 200 000 dollar mer än predikterat.
På det här viset kan vi ta fram residualen för varje spelare i data. Om regressionsekvationen är en bra beskrivning av data så kommer residualerna att ligga relativt tajt samlade kring noll och vi har liten spridning i residualerna (dvs. en låg varians i residualerna). Förklaringsgraden blir då nära 1. Men ju mer sanningen tenderar kasta från prediktionen desto större blir variansen i residualerna och desto lägre blir förklaringsgraden.
Logaritmerad skala
I kapitel 4 (“Sambandet mellan två variabler – regressionslinjen”) så diskuterade vi hur man tolkar koefficienterna i en regression där en eller båda variablerna mäts på en logaritmerad skala. I en multipel regression går det också bra att logga en eller flera variabler. Tolkningen är helt analog med den som gavs i kapitel 4:
| Regression | Tolkning |
|---|---|
| \[\widehat{ln(y)} = 2 + {\color{red}{0,1}} \times x\] | Då x ökar med en enhet så ökar y med \({\color{red}{0,1}}\times 100\) = 10 procent. |
| \[\widehat{ln(y)} = 2 + {\color{red}{0,1}} \times ln(x)\] | Då x ökar med en procent så ökar y med \(\color{red}{0,1}\) procent. |
| \[\widehat{y} = 2 + {\color{red}{0,1}} \times ln(x)\] | Då x ökar med en procent så ökar y med \({\color{red}{0,1}}/100\) = 0,001 enheter. |
Exempel. Se följande löneekvation:
\[\widehat{ln(lön)} = 0,250 + 0,102utb + 0,015erf\]
där utb mäter personens utbildning i antal år; erf mäter arbetserfarenhet i antal år. Då utbildningen ökar med ett år så ökar lönen i snitt med ~10 procent då vi kontrollerar för arbetserfarenhet. Då arbetserfarenheten ökar med ett år så ökar lönen i snitt med 1,5 procent då vi kontrollerar för utbildning.
Det går också bra att lägga in dummyvariabler i den här regressionen:
\[\widehat{ln(lön)} = 0,244 + 0,102utb + 0,015erf + 0,072kontor\]
där kontor är en dummy som antar värdet 1 för kontorsarbetare och 0 för övriga. Regressionen visar att kontorsarbetarna i snitt tjänar ~7 procent mer än övriga då vi kontrollerar för utbildning och arbetserfarenhet.
Presentation av resultaten
Hur presenterar man resultatet från en multipel regressionsanalys? Tabellen nedan visar ett exempel. Den är klippt ur artikeln Physical activity and GPA: Results from a national sample of Black students. Författarna har här kört flera regressioner, alltid med samma utfallsvariabel (GPA, grade point average eller snittbetyg). Här vill man ta reda på om det finns ett samband mellan att sporta utanför skoltid och snittbetyg. I kolumnen längst till vänster ges de oberoende variablerna, t.ex. “Participated in Sports” (en dummy för att man sportar utanför skoltid). I modell 1 har vi bara två oberoende variabler; i modell 2 och 3 har författarna successivt inkluderat fler oberoende variabler. Sedan har de gjort samma sak enbart för kvinnor (modell 4-6) och enbart för män (modell 7-9).
Så vad kan vi läsa ur den här tabellen? Jo, de intressantaste siffrorna är ju själva koefficienterna. Exempel: I modell 1 är koefficienten för “Participated in Sports” 0,34. De som sportar har alltså i snitt 0,34 enheter högre betyg än de som inte sportar, kontrollerat för “Hours spent on Extracurricular Activities”. Eller med andra ord: När vi jämför personer som har lika mycket aktiviteter utanför skolan, så ser vi att de som sportar har bättre betyg i snitt. Modell 1 utskrivet som en regression:
\[\widehat{gpa} = 2,84 + 0,34 \times particiated + 0,05 \times hours\]
(Du hittar interceptet på näst sista raden i samma kolumn.)
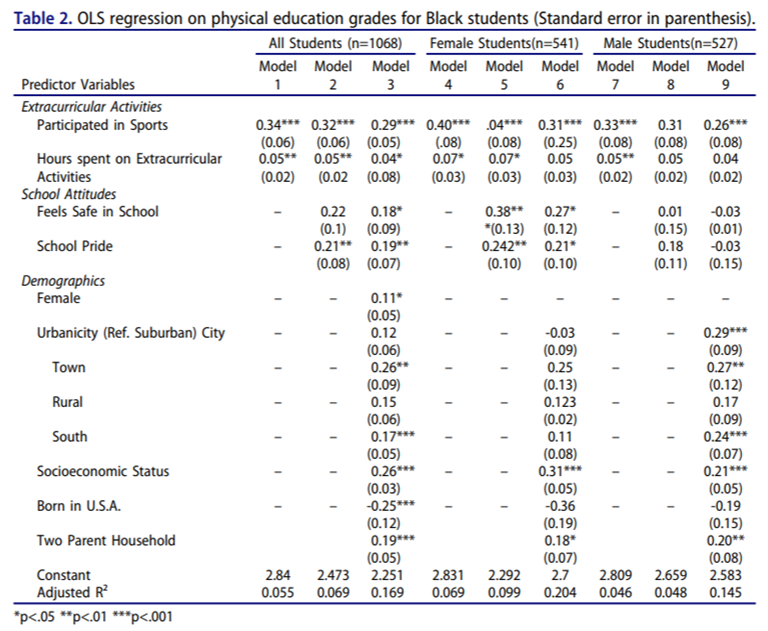
Är 0,34 då en stor effekt? Ja, den är nog större än den kanske kan verka. Snittbetyget ligger nämligen på 2,95 och standardavvikelsen är 1. Att sporta predikteras alltså höja snittbetyget med 34 procent av en standardavvikelse. Den här effekten är relativt stabil mellan olika modeller, dvs. den försvinner inte då författarna inkluderar fler kontrollvariabler (modell 2 och 3).
Under själva koefficienterna hittas också så kallade “standardfel” inom parenteser. Vi ska återkomma till vad dessa mäter i kapitel 8. Du kanske också noterar att de flesta koefficienterna märks ut med stjärnor. Exakt vad detta betyder kommer vi också att återkomma till senare!
Tabellen ovan är ett exempel på ett vanligt sätt att presentera regressioner. De oberoende variablerna ges i första kolumnen (och vanligtvis sätter man den viktigaste oberoende variabeln allra först). Tabellen innehåller också själva koefficienterna (här tillsammans med standardfel och stjärnor), förklaringsgraden och antalet observationer. Här ges förklaringsgraden (eller en justerad version) på sista raden; antalet observationer anges högst upp.
6.2 Regressioner med faktorvariabler
Exempel. Vi vill testa om lågkolhydratkost är effektivt som bantningsmetod. Ett antal överviktiga försökspersoner slumpas in i två jämnstora grupper; en som får äta lågkolhydratkost och en annan som får äta kalorisnål kost. I tabellen nedan visas data. Utfallsvariabeln är viktnedgång som mäter procentuell viktnedgång under loppet av sex månader. För enkelhetens skull tänker vi oss här att enbart tio personer ingår i studien. De som fick lågkolhydratkost (variabeln lågkol) är utmärkta i rött:
| Id | Kost | Lågkol | Viktnedgång |
|---|---|---|---|
| 1 | Kalorisnål | 0 | 1 |
| 2 | Kalorisnål | 0 | 7 |
| 3 | Kalorisnål | 0 | −2 |
| 4 | Kalorisnål | 0 | 10 |
| 5 | Kalorisnål | 0 | 4 |
| 6 | Lågkolhydrat | 1 | 6 |
| 7 | Lågkolhydrat | 1 | −3 |
| 8 | Lågkolhydrat | 1 | 10 |
| 9 | Lågkolhydrat | 1 | 8 |
| 10 | Lågkolhydrat | 1 | 14 |
Regressionslinjen ges av:
\[\widehat{viktnedgång} = 4 + 3 \times lågkol\]
De som åt kalorisnålt gick i genomsnitt ner 4 procent; de som åt lågkolhydratkost gick i genomsnitt ner 7 procent.
Anta nu att vi istället jämför kalorisnål kost med medelhavskost (variabeln medelhav) där de som fick denna kost är utmärkta i blått:
| Id | Kost | Medelhav | Viktnedgång |
|---|---|---|---|
| 1 | Kalorisnål | 0 | 1 |
| 2 | Kalorisnål | 0 | 7 |
| 3 | Kalorisnål | 0 | −2 |
| 4 | Kalorisnål | 0 | 10 |
| 5 | Kalorisnål | 0 | 4 |
| 6 | Medelhav | 1 | 5 |
| 7 | Medelhav | 1 | 5 |
| 8 | Medelhav | 1 | 0 |
| 9 | Medelhav | 1 | 6 |
| 10 | Medelhav | 1 | 9 |
Regressionslinjen ges av:
\[\widehat{viktnedgång} = 4 + 1 \times medelhav\]
De som åt kalorisnålt gick i genomsnitt ner 4 procent; de som åt medelhavskost gick i genomsnitt ner 5 procent.
Anta nu att vi har data för alla tre dieter. Såhär ser data ut då vi slått ihop det:
| Id | Kost | Lågkol | Medelhav | Viktnedgång |
|---|---|---|---|---|
| 1 | Kalorisnål | 0 | 0 | 1 |
| 2 | Kalorisnål | 0 | 0 | 7 |
| 3 | Kalorisnål | 0 | 0 | −2 |
| 4 | Kalorisnål | 0 | 0 | 10 |
| 5 | Kalorisnål | 0 | 0 | 4 |
| 6 | Lågkolhydrat | 1 | 0 | 6 |
| 7 | Lågkolhydrat | 1 | 0 | −3 |
| 8 | Lågkolhydrat | 1 | 0 | 10 |
| 9 | Lågkolhydrat | 1 | 0 | 8 |
| 10 | Lågkolhydrat | 1 | 0 | 14 |
| 11 | Medelhav | 0 | 1 | 5 |
| 12 | Medelhav | 0 | 1 | 5 |
| 13 | Medelhav | 0 | 1 | 0 |
| 14 | Medelhav | 0 | 1 | 6 |
| 15 | Medelhav | 0 | 1 | 9 |
Vi hade regressionerna:
\[\widehat{viktnedgång} = 4 + {\color{red}{3 \times lågkol}}\]
\[\widehat{viktnedgång} = 4 + {\color{blue}{1\times medelhav}}\]
Vi kan nu lika bra kombinera dessa två enkla regressioner i en multipel:
\[\widehat{viktnedgång} = 4 + {\color{red}{3 \times lågkol}} + {\color{blue}{1 \times medelhav}}\]
Den här regressionen visar exakt samma sak som de två enskilda. Vi kan också testa oss fram för att se att detta är fallet. Som tidigare har vi att den genomsnittliga viktnedgången är 4 procent bland dem som åt kalorisnålt:
\[\widehat{viktnedgång} = 4 + 3 \times \underbrace{lågkol}_{= 0} + 1 \times \underbrace{medelhav}_{= 0} = 4\]
Och att den genomsnittliga viktnedgången är 7 procent bland dem som åt lågkolhydratkost:
\[\widehat{viktnedgång} = 4 + 3 \times \underbrace{lågkol}_{= 1} + 1 \times \underbrace{medelhav}_{= 0} = 4 + 3 = 7\]
Bland dem som åt medelhavskost är den genomsnittliga viktnedgången 5 procent:
\[\widehat{viktnedgång} = 4 + 3 \times \underbrace{lågkol}_{= 0} + 1 \times \underbrace{medelhav}_{= 1} = 4 + 1 = 5\]
Notera här att lågkolhydratkost och medelhavskost jämförs med kalorisnål kost: Koefficienten för lågkol visar att lågkolhydratgruppen i snitt gick ner 3 procentenheter mer än de som åt kalorisnålt; koefficienten för medelhav visar att de som åt medelhavskost i snitt gick ner 1 procentenhet mer än de som åt kalorisnålt. Interceptet visar att de som åt kalorisnålt i snitt gick ner 4 procent. Av den här anledningen kallar man ibland den kalorisnåla gruppen för referensgrupp. Figuren nedan illustrerar detta:
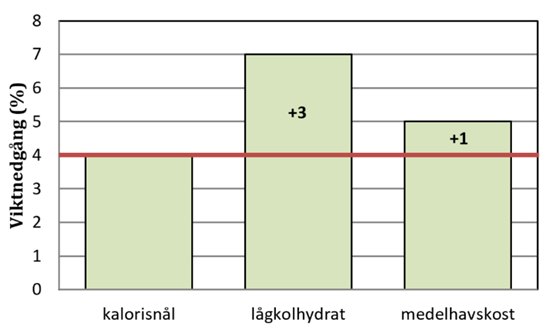
Det finns ingenting som säger att vi bör använda just kalorisnål kost som referensgrupp. Vi kunde lika bra välja en av de andra dieterna. Säg att vi istället valde lågkolhydratkost som referens. Då får vi regressionen:
\[\widehat{viktnedgång} = 7 - 3 \times kalorisnål - 2 \times medelhav\]
Den här regressionen visar att de som åt kalorisnålt i snitt gick ner tre procentenheter mindre än de som åt lågkolhydratkost; de som åt medelhavskost gick i snitt ner två procentenheter mindre än de som åt lågkolhydratkost. (Men det här visste vi ju redan.)
Så vad är poängen med att använda en regression för att beskriva det som bara är skillnaden mellan tre medelvärden? Jo, det här exemplet visar hur vi kan ta in en kvalitativ variabel (kost) i en regression genom att göra om den till en rad dummyvariabler (lågkol, medelhav). Ibland kallar man en sådan kvalitativ variabel (kost) för en faktor och därifrån kommer namnet för det här delkapitlet.
Om vi kör den här regressionen i ett statistiskt programpaket så inkluderar vi två av dieterna som dummyvariabler. Nedan har vi använt lågkol och medelhav; utfallet är viktnedgång:
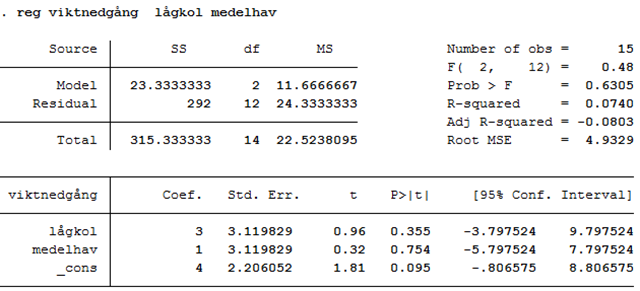
Notera att förklaringsgraden (R-squared) har värdet 0,0740: 7,4 procent av variationen i viktnedgång kan förklaras av kosten.
Vi ska ännu se på ett annat exempel:
Exempel. Hur varierar tentresultat beroende på hur mycket man sovit natten innan tenten? Efter en stor tentamen låter vi studenterna fylla i en enkät där de uppskattar hur många timmar de sov natten innan. De kan välja mellan följande alternativ: 0-2 timmar, 2-4 timmar, 4-6 timmar och 6+ timmar. I tabellen nedan visas ett utdrag av data. Variabeln sömn är kodad enligt följande:
1 = 0-2 timmar
2 = 2-4 timmar
3 = 4-6 timmar
4 = 6+ timmar
Variabeln resultat mäter procenten rätt på tenten:
| Id | Sömn | Resultat |
|---|---|---|
| 1 | 1 | 42 |
| 2 | 3 | 54 |
| 3 | 4 | 93 |
| 4 | 4 | 68 |
| 5 | 2 | 52 |
| … | … | … |
| 100 | 4 | 75 |
Här har vi beskrivit genomsnittligt resultat för varje “sömngrupp”:
| Sömn | Medelvärde | obs. |
|---|---|---|
| 1 (0–2 timmar) | 49,8 | 11 |
| 2 (2–4 timmar) | 61,9 | 8 |
| 3 (4–6 timmar) | 66,1 | 31 |
| 4 (6+ timmar) | 78,0 | 50 |
Samma information som presenteras i tabellen ovan kan vi också beskriva genom en regression:
\[\widehat{resultat} = 49,8 + {\color{red}{12,1}}sömn2 + {\color{blue}{16,3}}sömn3 + {\color{green}{28,2}}sömn4\]
I regressionen ovan är sömn2 en dummy som antar värdet 1 för dem som sov 2-4 timmar och värdet 0 för övriga; sömn3 är en dummy som antar värdet 1 för dem som sov 4-6 timmar och värdet 0 för övriga; sömn4 är en dummy för dem som sov 6+ timmar och värdet 0 för övriga. Referensgruppen är de som sovit 0-2 timmar.
Precis som i tabellen ovan så visar den här regressionen att personer som sov 2-4 timmar i snitt skrev 12,1 procentenheter bättre än de som sov 0-2 timmar; personer som sov 4-6 timmar skrev i snitt 16,3 procentenheter bättre än de som sov 0-2 timmar; personer som sov 6+ timmar skrev i snitt 28,2 procentenheter bättre än de som sov 0-2 timmar; de som sov 0-2 timmar skrev i snitt 49,8 procent.
Vi kan också se att de här tolkningarna stämmer genom att jämföra genomsnittligt tentresultat mellan olika grupper:
De som sov 0-2 timmar skrev i snitt 49,8 procent rätt:
\[\widehat{resultat} = 49,8 + {\color{red}{12,1}}\underbrace{sömn2}_{= 0} + {\color{blue}{16,3}}\underbrace{sömn3}_{= 0} + {\color{green}{28,2}}\underbrace{sömn4}_{= 0} = 49,8\]
De som sov 2-4 timmar (sömn2 = 1) skrev i snitt 12,1 procentenheter bättre än de som sov 0-2 timmar:
\[\widehat{resultat} = 49,8 + {\color{red}{12,1}}\underbrace{sömn2}_{= 1} + {\color{blue}{16,3}}\underbrace{sömn3}_{= 0} + {\color{green}{28,2}}\underbrace{sömn4}_{= 0} = 49,8 + 12,1\]
De som sov 4-6 timmar (sömn3 = 1) skrev i snitt 16,3 procentenheter bättre än de som sov 0-2 timmar:
\[\widehat{resultat} = 49,8 + {\color{red}{12,1}}\underbrace{sömn2}_{= 0} + {\color{blue}{16,3}}\underbrace{sömn3}_{= 1} + {\color{green}{28,2}}\underbrace{sömn4}_{= 0} = 49,8 + 16,3\]
De som sov 6+ timmar (sömn4 = 1) skrev i snitt 28,2 procentenheter bättre än de som sov 0-2 timmar:
\[\widehat{resultat} = 49,8 + {\color{red}{12,1}}\underbrace{sömn2}_{= 0} + {\color{blue}{16,3}}\underbrace{sömn3}_{= 0} + {\color{green}{28,2}}\underbrace{sömn4}_{= 1} = 49,8 + 28,2\]
Nedan visas ett utdrag av data, samt datautskriften från en regression där vi inkluderat variablerna sömn2, sömn3 och sömn4 som oberoende variabler:
| Id | Sömn | Sömn2 | Sömn3 | Sömn4 | Resultat |
|---|---|---|---|---|---|
| 1 | 1 | 0 | 0 | 0 | 42 |
| 2 | 3 | 0 | 1 | 0 | 54 |
| 3 | 4 | 0 | 0 | 1 | 93 |
| 4 | 4 | 0 | 0 | 1 | 68 |
| 5 | 2 | 1 | 0 | 0 | 52 |
| … | … | … | … | … | … |
| 100 | 4 | 0 | 0 | 1 | 75 |
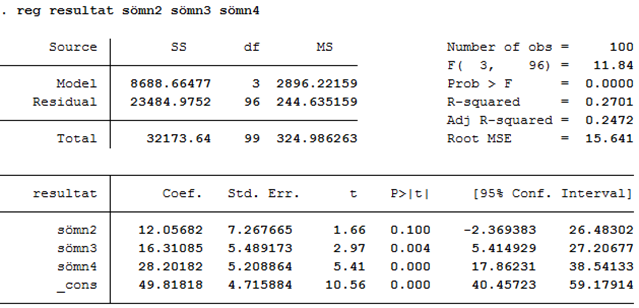
Anta att vi nu också frågat studenterna hur många timmar de jobbat med kursen per vecka (variabeln timmar). Ett utdrag av data ges nedan:
| Id | Sömn | Sömn2 | Sömn3 | Sömn4 | Timmar | Resultat |
|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 0 | 0 | 8 | 42 |
| 2 | 3 | 0 | 1 | 0 | 6 | 54 |
| 3 | 4 | 0 | 0 | 1 | 11 | 93 |
| 4 | 4 | 0 | 0 | 1 | 6 | 68 |
| 5 | 2 | 1 | 0 | 0 | 10 | 52 |
| … | … | … | … | … | … | … |
| 100 | 4 | 0 | 0 | 1 | 10 | 75 |
Vi har då möjlighet att ställa oss följande fråga: Om vi jämför studenter som jobbat lika mycket, finns det då fortfarande skillnader i resultat beroende på sömngrupp? Vi kan få en uppskattning av svaret på den här frågan genom att inkludera antalet arbetstimmar (timmar) som en oberoende variabel i regressionen:
\[\widehat{resultat} = a + b_{1}sömn2 + b_{2}sömn3 + b_{3}sömn4 + b_{4}timmar\]
Här är utskriften då vi kör regressionen med hjälp av statistikprogrammet STATA:
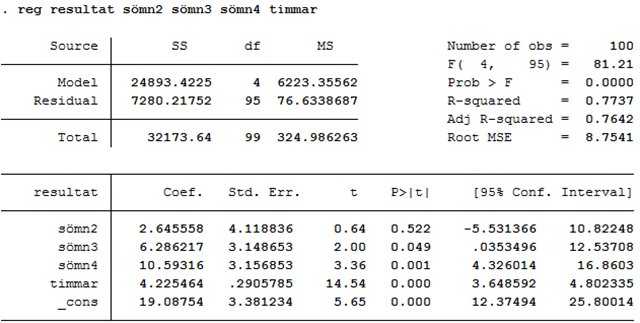
Regressionsekvationen:
\[\widehat{resultat} = 19,1 + 2,6sömn2 + 6,3sömn3 + 10,6sömn4 + 4,2timmar\]
Som du märker så minskar nu skillnaderna mellan sömngrupperna. Exempel: Tidigare såg vi att de som sovit 6+ timmar i snitt skrivit 28,2 procentenheter bättre än de som sovit 0-2 timmar. Men då vi kontrollerar för antalet arbetstimmar så sjunker skillnaden till 10,6 procentenheter. Det här betyder att personer som sovit 6+ timmar i snitt jobbat mer under kursens lopp, vilket delvis förklarar varför de klarar sig bättre på tenten.
Precis som tidigare så kan vi använda den här regressionen för att göra prediktioner. Exempel: För en person som sovit 4-6 timmar (sömn3 = 1) och jobbat 12 timmar per vecka så predikteras tentresultatet bli 75,8 procent:
\[\widehat{resultat} = {\color{red}{19,1}} + 2,6\underbrace{sömn2}_{= 0} + {\color{green}{6,3}}\underbrace{sömn3}_{= 1} + 10,6\underbrace{sömn4}_{= 0} + {\color{blue}{4,2}}\underbrace{timmar}_{= 12}\]
\[= {\color{red}{19,1}} + {\color{green}{6,3}} + {\color{blue}{4,2 \times 12}} = 75,8\]
Från regressionsutskriften ser vi också att förklaringsgraden har värdet 0,77: 77 procent av variationen i tentamensresultat kan förklaras av sömn och antal arbetstimmar.
I det här exemplet kontrollerade vi för antal arbetstimmar, men inget hindrar oss från att kontrollera för fler variabler (t.ex. kön, huvudämne, genomsnittligt resultat på tidigare kurser, …).
Grafisk presentation
Spridningsdiagrammen nedan visar sambandet mellan resultat och arbetstimmar för varje enskild sömngrupp. Exempel: Regressionslinjen i den första gruppen (0-2 sovtimmar) fås som:
\[\widehat{resultat} = 19,1 + 2,6\underbrace{sömn2}_{= 0} + 6,3\underbrace{sömn3}_{= 0} + 10,6\underbrace{sömn4}_{= 0} + 4,2timmar\]
\[= 19,1 + 4,2timmar\]
Vi har ritat ut denna regressionslinje tillsammans med observationerna för den här gruppen i spridningsdiagrammet nere till vänster. På motsvarande sätt har vi fått regressionslinjerna i de andra tre sömngrupperna. Exempel: Regressionslinjen i den andra gruppen (2-4 timmar) fås som:
\[\widehat{resultat} = 19,1 + 2,6\underbrace{sömn2}_{= 1} + 6,3\underbrace{sömn3}_{= 0} + 10,6\underbrace{sömn4}_{= 0} + 4,2timmar\]
\[= 19,1 + 2,6 + 4,2timmar = 21,7 + 4,2timmar\]
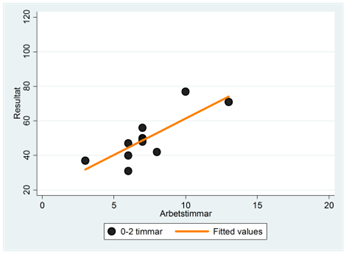
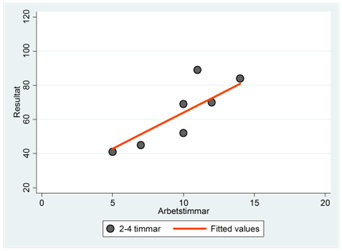
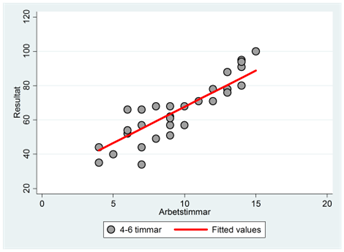
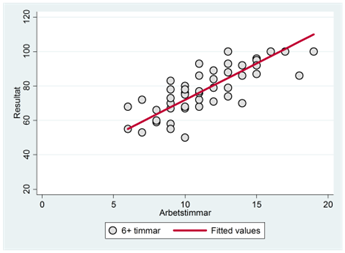
När vi kombinerar dessa fyra spridningsdiagram i ett så blir resultatet:
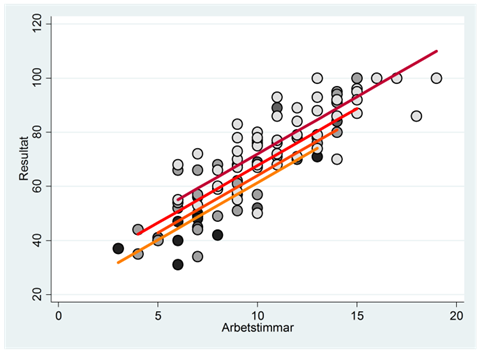
Det vertikala avståndet mellan två linjer visar skillnaden i genomsnittligt resultat mellan dessa sömngrupper då vi kontrollerat för antalet arbetstimmar.
Som du märker så är det här diagrammet ganska svårläst, och skulle vi mäta sovtiden genom fler grupper så skulle spridningsdiagrammet bli ännu svårare att läsa. Orsaken är att det här diagrammet illustrerar allt: hur tentamensresultat varierar med antal arbetstimmar och beroende på sömngrupp, samt den allmänna spridningen i data. Vi kan få ett tydligare diagram genom att enbart illustrera en aspekt; den aspekt som är av huvudsakligt intresse för oss. I det här exemplet är vi först och främst intresserade av skillnader i tentamensresultat beroende på sömn. Figuren nedan illustrerar detta; den visar hur genomsnittligt tentamensresultat varierar beroende på sömngrupp då vi kontrollerat för antalet arbetstimmar. På engelska kallas detta för ett profile plot vilket kan översättas till profildiagram på svenska.
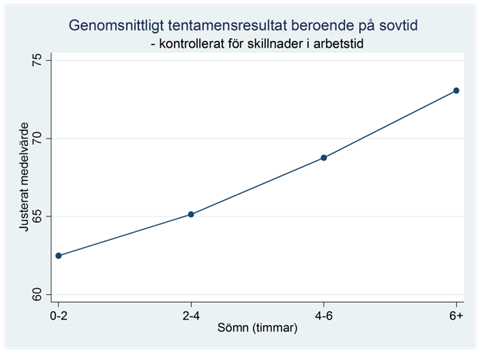
Hur har vi åstadkommit det här diagrammet? Jo, vi utgår från regressionen:
\[\widehat{resultat} = 19,1 + 2,6sömn2 + 6,3sömn3 + 10,6sömn4 + 4,2timmar\]
Den genomsnittliga studenten har pluggat 10,3 timmar per vecka. För en genomsnittlig student så varierar tentamensresultatet med sömn enligt:
\[\widehat{resultat} = 19,1 + 2,6sömn2 + 6,3sömn3 + 10,6sömn4 + 4,2\underbrace{timmar}_{= 10,3}\]
\[\approx 19,1 + 2,6sömn2 + 6,3sömn3 + 10,6sömn4 + 43,3\]
\[= 62,4 + 2,6sömn2 + 6,3sömn3 + 10,6sömn4\]
Vi kan nu använda den här regressionen för att prediktera tentamensresultatet för de fyra olika sömngrupperna. En genomsnittlig student som sovit 0-2 timmar predikteras skriva 62,4 procent:
\[\widehat{resultat} = 62,4 + 2,6\underbrace{sömn2}_{= 0} + 6,3\underbrace{sömn3}_{= 0} + 10,6\underbrace{sömn4}_{= 0} = 62,4\]
En genomsnittlig student som sovit 2-4 timmar (sömn2 = 1) predikteras skriva 65 procent:
\[\widehat{resultat} = 62,4 + 2,6\underbrace{sömn2}_{= 1} + 6,3\underbrace{sömn3}_{= 0} + 10,6\underbrace{sömn4}_{= 0} = 65,0\]
Och på motsvarande sätt kan vi räkna ut att en genomsnittlig student som sovit 4-6 timmar predikteras skriva 68,7 procent rätt och att en som sovit 6+ timmar predikteras skriva 73,0 procent rätt.
Dessa fyra prediktioner (62,4; 65,0; 68,7 och 73,0) är uppskattningar av hur genomsnittligt tentamensresultat varierar beroende på sömngrupp för en genomsnittlig student som pluggat 10,3 timmar per vecka. Det är dessa prediktioner som visas i profildiagrammet ovan.
Appendix
Formlerna bakom regressionsekvationen
Vi ska börja med att jämföra med en enkel regression. Vi har ett sampel och vill beräkna värdena för a och b i regressionslinjen: \(\widehat{y} = a + bx\). Vi använder formlerna:
\[b = \frac{kovariansen\ mellan\ x\ och\ y}{variansen\ för\ x}\]
\[a = \overline{y} - b\overline{x}\]
Anta nu en regression med två oberoende variabler: \(\widehat{y} = a + b_{1}x_{1} + b_{2}x_{2}\). Vi kan räkna ut värdet för b1 som:
\[b_{1} = \frac{kovariansen\ mellan\ r\ och\ y}{variansen\ för\ r}\]
där r är residualerna från en regression med x1 som beroende variabel och x2 som oberoende variabel. För att få fram värdet för b1 kan vi med andra ord köra en regression med y som beroende variabel och r som oberoende variabel. Koefficienten för x2 (b2) beräknas på motsvarande sätt. Interceptet ges av:
\[a = \overline{y} - b_{1}{\overline{x}}_{1} - b_{2}{\overline{x}}_{2}\]
Om vi har fler än två oberoende variabler, säg tre, så får vi regressionsekvationen på motsvarande sätt. Exempel: \(\widehat{y} = a + b_{1}x_{1} + b_{2}x_{2} + b_{3}x_{3}.\)
\[b_{1} = \frac{kovariansen\ mellan\ r\ och\ y}{variansen\ för\ r}\]
där r är residualerna från en regression med x1 som beroende variabel och x2 och x3 som oberoende variabler. Interceptet ges då av:
\[a = \overline{y} - b_{1}{\overline{x}}_{1} - b_{2}{\overline{x}}_{2} - b_{3}{\overline{x}}_{3}\]
Sammanfattning
Övningsuppgifter
Att kontrollera för andra faktorer
- Regressionen nedan visar hur kvinnors arbetsmarknadsdeltagande varierar beroende på om de har småbarn eller inte. Datamaterialet gäller 753 amerikanska kvinnor år 1975. Variabeln timmar mäter antalet timmar som kvinnan jobbade under året; småbarn är en dummy som antar värdet 1 om hon hade barn i åldrarna 0-5 år och annars värdet 0:
\[\widehat{timmar} = 836 - 488småbarn\]
Hur många timmar jobbade i genomsnitt en kvinna utan småbarn? En kvinna med småbarn?
Vi kontrollerar nu också för kvinnans ålder och får följande resultat:
Tolka koefficienten för småbarn.
Tolka koefficienten för ålder.
Prediktera antalet arbetstimmar för en 30-årig kvinna utan småbarn.
Är småbarnsföräldrar i snitt yngre eller äldre än de som inte har småbarn? Förklara! (Kan du också säga exakt hur stor skillnaden i ålder är mellan grupperna?)
- Vi mäter skillnaden i lön mellan män och kvinnor år 2010. Regressionen nedan visar att männen i samplet i genomsnitt tjänade 3000 euro, och att kvinnorna i snitt tjänade 500 euro mindre:
\[\widehat{{lön}_{2010}} = 3000 - 500kvinna\]
Vi kontrollerar nu för personernas löner år 2009:
\[\widehat{{lön}_{2010}} = a + b_{1}kvinna + {b_{2}lön}_{2009}\]
Vilket av följande alternativ beskriver bäst vad som händer med koefficienten för kvinna?
b1 kommer fortsättningsvis att ha värdet -500.
b1 mäter nu löneskillnaden mellan kvinnor och män år
b1 kommer antagligen att få ett värde närmare noll.
b1 kommer antagligen att få ett mer negativt värde.
- Studenter som går på många föreläsningar har i snitt bättre tentamensresultat. Men hjälper verkligen föreläsningarna eller är det istället de duktigaste studenterna som går på flest föreläsningar? Du vill nu undersöka detta. Du har tillgång till ett datamaterial som innehåller följande variabler: Studentens poäng på kurstenten (variabeln poäng), antalet föreläsningar som studenten deltog i (variabeln deltagande) och studentens poäng på inträdesförhöret till universitetet (variabeln inträde). Data samlas in för 100 studenter på deras första grundkurs vid ÅA.
Hur skulle du mäta om föreläsningarna hjälper? Ställ upp en regressionsekvation som visar vilken variabel som är beroende, och vilken eller vilka variabler som är oberoende.
Se fråga a: Vilket resultat kan du förvänta dig att se om det är så att föreläsningarna hjälper? Använd här din regressionsekvation från uppgift a: Vilket tecken (positivt/negativt/noll) skulle den relevanta koefficienten anta?
- Det finns ett klart samband mellan hur länge föräldrar har gått i skolan och hur länge deras barn går i skolan. Spridningsdiagrammet nedan visar sambandet för 30-åriga amerikaner år 1976. På y-axeln har vi individens utbildning mätt i antal år (utb); på x-axeln har vi föräldrarnas genomsnittliga utbildningsmängd (forutb). Vi har också ritat in regressionslinjen i diagrammet, där
\[\widehat{utb} = 10,11 + 0,40forutb\]
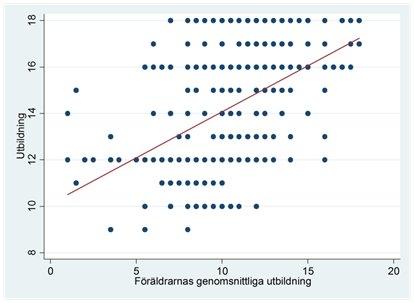
- Anta att hela sambandet kan förklaras av att barn till högutbildade i genomsnitt är smartare än barn till lågutbildade, och att högintelligenta personer i sin tur utbildar sig längre. Vi kontrollerar nu för iq och kör regressionen:
Ungefär vilket värde antar då koefficienten b1?
- Nedan ges det egentliga resultatet:
Har barn till högutbildade i snitt högre intelligenskvot, samma intelligenskvot eller lägre intelligenskvot än barn till lågutbildade? Förklara!
Hur mycket predikteras utbildningsmängden öka om intelligenskvoten ökar med 1 poäng (och vi håller föräldrarnas utbildning konstant)? Och om intelligenskvoten ökar 10 poäng?
Hur mycket ska intelligenskvoten öka för att utbildningsmängden ska öka med ett år?
Vi kontrollerar nu också för om personen bodde nära ett universitet i tonåren (variabeln nära som antar värdet 1 för dem som bodde nära ett universitet och 0 för övriga):
\[\widehat{utb} = 3,55 + 0,27forutb + 0,07iq + 0,22nära\]
En av personerna i data har 12 års utbildning. Personen har en intelligenskvot på 103 poäng, föräldrarnas utbildning är 13 år och personen bodde inte nära ett universitet i tonåren. Hur stor är residualen för den här personen?
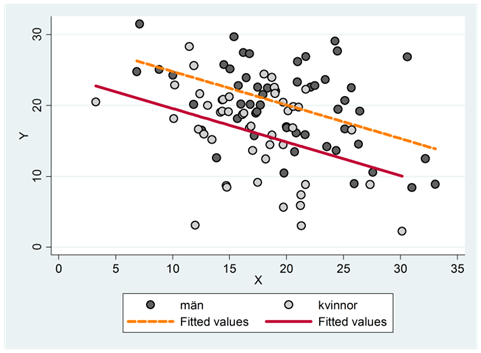
- Vi kör en regression som beskriver hur utfallsvariabeln varierar beroende på kön och en annan oberoende variabel: \(\widehat{y} = a + b_{1}kvinna + b_{2}x\), där kvinna är en dummy som antar värdet 1 för kvinnor och 0 för män. Spridningsdiagrammet nedan illustrerar data grafiskt. Vilket av följande fyra påståenden är sanna:
b1 har ett negativt värde och b2 har ett negativt värde
b1 har ett negativt värde och b2 har ett positivt värde
b1 har positivt värde och b2 har ett negativt värde
b1 har ett positivt värde och b2 har ett positivt värde
- Hur stiger VD:ns lön med antalet år på posten? För att besvara denna fråga använder vi ett sampel för 177 amerikanska företag år 1990. I regressionen nedan mäter variabeln lön VD:ns lön i tusentals dollar; erfarenhet mäter antalet år på posten och vinst mäter företagets vinst i miljoner dollar:
\[ \widehat{lön} = 646,43 + 12,45\,erfarenhet + 0,588\,vinst \qquad R^{2} = 0,178 \]
Förklaringsgraden är 0,178. Tolka!
Anta att residualen vore noll för varje observation i data. Hur stor vore då förklaringsgraden?
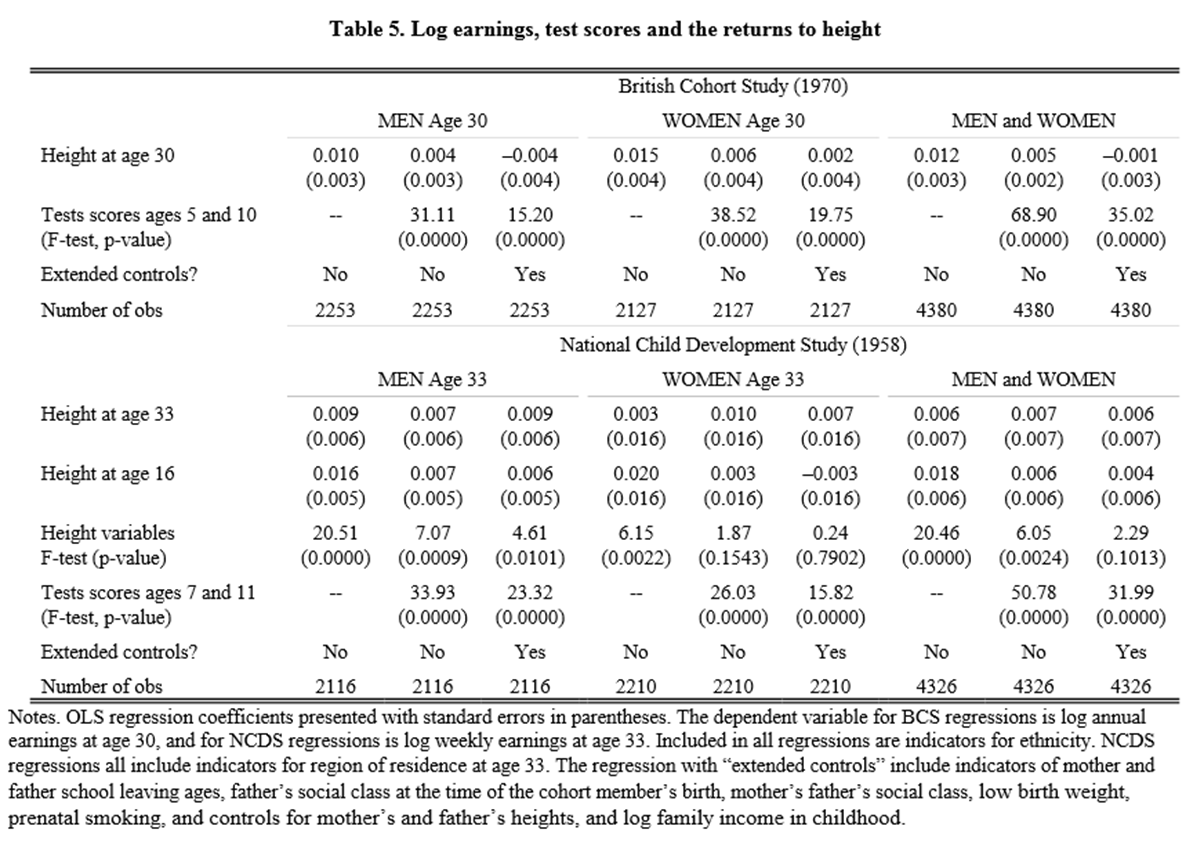
- Tabellen nedan är klippt ur artikeln Stature and Status: Health, Ability and Labor Market Outcomes. Utfallsvariabeln är loggad lön (den naturliga logaritmen).
Se samplet “British Cohort Study (1970)” och “MEN age 30”. Tolka koefficienten för height at age 30, där längden mäts i tum. Använd då resultatet från regressionen där man inte kontrollerat för testresultat i ung ålder eller övriga kontrollvariabler (extended controls).
Abstraktet är klippt ur samma artikel. Läs och ta fasta på det som är understruket i rött. Förklara hur resultaten i tabellen stödjer detta uttalande. (Använd då samplet “British Cohort Study (1970)”.)

Regressioner med faktorvariabler
- Tabellen nedan beskriver genomsnittligt antal sjukdagar per år i tre olika yrkesgrupper.
| Yrke | Medelvärde | obs. |
|---|---|---|
| Lärare | 15 | 563 |
| Kassabiträde | 20 | 368 |
| Bibliotekarie | 10 | 247 |
Vilken eller vilka regressionsekvationer beskriver dessa skillnader?
\(\widehat{sjukdagar} = 10 + 15lärare + 20kassabiträde + 10bibliotekarie\)
\(\widehat{sjukdagar} = 10 + 5lärare + 10kassabiträde - 5bibliotekarie\)
\(\widehat{sjukdagar} = 15 + 20kassabiträde + 10bibliotekare\)
\(\widehat{sjukdagar} = 15 + 5kassabiträde - 5bibliotekare\)
\(\widehat{sjukdagar} = 10 + 5lärare + 10kassabiträde\)
(I alla regressioner ovan är lärare en dummy som antar värdet 1 för lärare och 0 för övriga; kassabiträde är en dummy som antar värdet 1 för kassabiträden och 0 för övriga; bibliotekarie är en dummy som antar värdet 1 för bibliotekarier och 0 för övriga.)
- Du vill mäta sambandet mellan skatteprocent och arbetslöshetsgrad i världens länder:
\[\widehat{arbetslöshet} = a + b \times skatteprocent\]
Du vill nu ännu kontrollera för världsdel, där alla länder i data ligger i antingen Afrika, Asien, Europa, Nordamerika eller Sydamerika. Formulera en regressionsekvation som kontrollerar för världsdel. (Använd regressionsekvationen ovan och utvidga med lämpliga oberoende variabler. Namnge dessa själv och beskriv också hur variablerna är kodade.)
- Regressionen nedan visar hur bmi varierar beroende på etnicitet och ålder. Bmi är ett mått som antar högre värden ju mer man väger i förhållande till sin längd (ett bmi på 18,5-25 räknas som normalviktig; lägre värden som underviktig och högre värden som överviktig). Etnicitet mäts genom tre kategorier (vit, svart och övriga). I regressionen nedan är svart en dummy för svarta och övrig en dummy som antar värdet 1 för personer som varken är vita eller svarta och värdet 0 för dem som är vita eller svarta. Referensgruppen är vita personer. Ålder mäter personernas åldrar i antal år. Data kommer från en amerikansk enkätstudie med 10 351 respondenter.
\[\widehat{bmi} = 23,1 + 1,4svart - 1,2övrig + 0,05ålder\]
Prediktera bmi för en vit person som är 30 år gammal.
Vilken etnisk grupp väger i snitt som mest då vi kontrollerat för ålder? Vilken etnisk grupp väger i snitt som minst då vi kontrollerat för ålder?
Förklaringsgraden är 0,038. Tolka!
Visa hur man kan illustrera sambandet mellan bmi och etncitet genom ett profildiagram (använd mallen nedan). Diagrammet ska visa hur genomsnittlig bmi varierar beroende på etnicitet för en genomsnittlig person som är 48 år gammal.